树链剖分用于将树分割成若干条链的形式,以维护树上路径的信息。
具体来说,将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
树链剖分有很多种形式,本文要讲的是其中的轻重链剖分。
树链剖分本质上就是把链从树上砍下来,然后放到树状数组或线段树上来维护。
轻重链剖分
我们给出一些定义:
定义 重子节点 表示其子节点中 子树最大 的子结点。如果有多个子树最大的子结点,取其一。如果没有子节点,就无重子节点。
定义 轻子节点 表示剩余服务器托管网的所有子结点。
从这个结点到重子节点的边为 重边。
到其他轻子节点的边为 轻边。
若干条首尾衔接的重边构成 重链。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链。
如图:
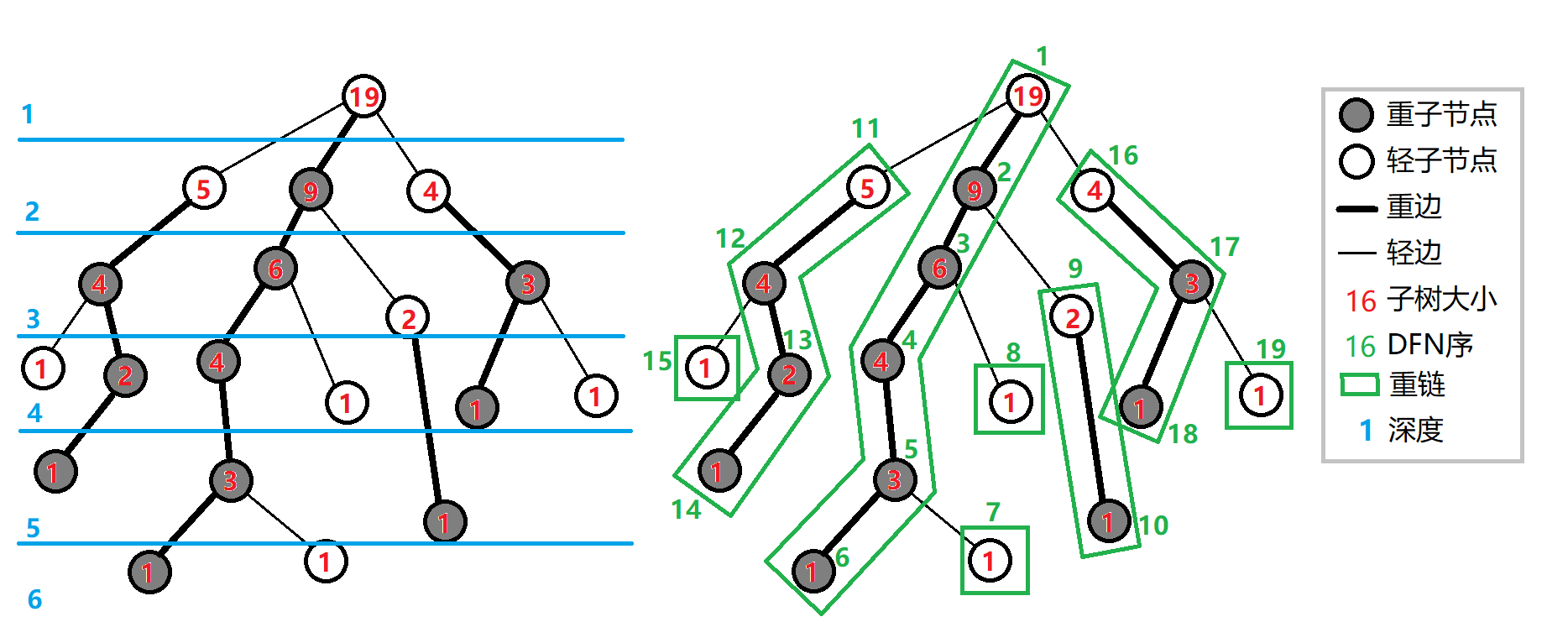
图片来自 (texttt{OI-Wiki})。
实现
要进行树链剖分,得先有一棵树,通过一个 dfs 来得到所有的子树大小、重儿子以及每个结点的深度。
void dfs(int u, int fat) {
siz[u] = 1;
fa[u] = fat;
dep[u] = dep[fat] + 1;
for (int v : e[u]) {
if (v == fat) continue ;
dfs(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) {
son[u] = v;
}
}
}
得到这些信息后,我们就要把树分成好多的链,通过另一个 dfs 来确定好链顶,有时我们要用线段树或树状数组来维护这些链,所以可能还要维护在线段树上的位置(dfs 序)等信息。
void getpos(int u, int top) {
dfn[u] = ++ tim; // 在线段树上的位置 (dfs 序)
pos[tim] = u; // 线段树这个位置所代表的节点
tp[u] = top; // 链顶
if (!son[u]) return ;
getpos(son[u], top); // 优先跑重儿子
for (int v : e[u]) {
if (v == fa[u] || v == son[u]) continue ;
getpos(v, v); // 轻儿子再单独分链
}
}
到这里,处理部分就完成了,接下来就是根据题目来对这些链进行处理了,可以使用线段树、树状数组等数据结构来维护链的信息,也可以利用跳链顶的优秀复杂度求 LCA 等。
例题
P3384 【模板】重链剖分/树链剖分 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
模板题。
要求我们对链上节点的权值进行修改、求和,以及对子树内的所有节点进行修改、求和,我们使用线段树来进行维护。
对于链上的操作,由于我们已经把链都摆在了线段树上,所以只需要对线段树进行区间操作即可。对于子树的操作,根据 dfs 序的性质,一棵子树在 dfs 序上的范围是 ([dfn_{rt}, dfn_{rt} + siz_{rt} – 1]),对这个区间进行区间操作即可。
void Modify(int x, int y, ll z) {
while (tp[x] != tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
modify(1, 1, n, dfn[x], dfn[y], z);
return ;
}
ll Query(int x, int y) {
ll ans = 0;
while (tp[x] != tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
ans = (ans + query(1, 1, n, dfn[x], dfn[y])) % mod;
return ans;
}
这两段代码就是跳链的过程,可以这样理解一下,如果两个节点的链顶不相同,说明他们不在同一条链中,我们让链顶深度大的节点向上跳(这样可以防止跳过头),在跳之前,先对这段链的信息进行修改维护,也就是 Modify 中的 modify 函数和 Query 中的 query 函数,然后,跳到这个链顶的父亲,离开这条链,以此继续,直到这两个节点链顶一样时(即在同一条链上时),对这两个节点之间的链进行操作,退出函数。
// The code was written by yifan, and yifan is neutral!!!
#include
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i = (b); i -= (c))
#define Mod(x) ((x) >= mod ? (x) %= mod : (x))
template
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch e[N];
struct seg {
int len;
ll val, tag;
} t[N siz[son[u]]) {
son[u] = v;
}
}
}
void getpos(int u, int top) {
dfn[u] = ++ tim;
pos[tim] = u;
tp[u] = top;
if (!son[u]) return ;
getpos(son[u], top);
for (int v : e[u]) {
if (v == fa[u] || v == son[u]) continue ;
getpos(v, v);
}
}
#define ls (u > 1)
void pushup(int u) {
t[u].val = (t[ls].val + t[rs].val) % mod;
}
void pushdown(int u, int l, int r) {
if (!t[u].tag) return ;
if (l == r) {
t[u].tag = 0;
return ;
}
t[ls].tag = (t[ls].tag + t[u].tag) % mod;
t[ls].val = (t[ls].val + t[u].tag * t[ls].len % mod) % mod;
t[rs].tag = (t[rs].tag + t[u].tag) % mod;
t[rs].val = (t[rs].val + t[u].tag * t[rs].len % mod) % mod;
t[u].tag = 0;
return ;
}
void build(int u, int l, int r) {
t[u].tag = 0;
t[u].len = r - l + 1;
if (l == r) {
t[u].val = val[pos[l]];
return ;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(u);
}
void modify(int u, int l, int r, int lr, int rr, ll v) {
if (lr mid) {
modify(rs, mid + 1, r, lr, rr, v);
}
pushup(u);
}
void Modify(int x, int y, ll z) {
while (tp[x] != tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
modify(1, 1, n, dfn[x], dfn[y], z);
return ;
}
ll query(int u, int l, int r, int lr, int rr) {
if (lr mid) {
ans = (ans + query(rs, mid + 1, r, lr, rr)) % mod;
}
return ans;
}
ll Query(int x, int y) {
ll ans = 0;
while (tp[x] != tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
ans = (ans + query(1, 1, n, dfn[x], dfn[y])) % mod;
return ans;
}
#undef ls
#undef rs
#undef mid
int main() {
n = read(), m = read();
rt = read(), mod = read();
rep (i, 1, n, 1) {
val[i] = read();
}
int x, y;
rep (i, 1, n - 1, 1) {
x = read(), y = read();
e[x].emplace_back(y);
e[y].emplace_back(x);
}
dfs(rt, 0);
getpos(rt, rt);
build(1, 1, n);
int op, z;
rep (i, 1, m, 1) {
op = read(), x = read();
if (op == 1) {
y = read(), z = read();
Modify(x, y, z);
}
if (op == 2) {
y = read();
cout ();
modify(1, 1, n, dfn[x], dfn[x] + siz[x] - 1, z);
}
if (op == 4) {
cout P4211 [LNOI2014] LCA – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
询问 LCA 的深度,其实就是在树上差分中,一个节点权值 (+ 1),另一个点求该节点到根节点的路径和。在树链剖分中,就是将根节点到一个节点这条链上所有的点 (+ 1),另一个节点求该节点到根节点的路径的权值和。
可以经询问进行离线处理,离线来完成这道题,具体看代码。
//The code was written by yifan, and yifan is neutral!!!
#include
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define lowbit(x) (x & (-x))
#define ls (u > 1)
template
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch e[N];
struct ask {
int be, R, z;
bool fg;
int operator siz[son[u]]) {
son[u] = v;
}
}
}
void gettop(int u, int Top) {
static int t = 0;
tp[u] = Top;
dfn[u] = ++ t;
pos[t] = u;
if (!son[u]) return ;
gettop(son[u], Top);
for (int v : e[u]) {
if (v == fa[u] || v == son[u]) continue ;
gettop(v, v);
}
}
void color(int u, int l, int r, int co) {
t[u].val = (t[u].val + (r - l + 1) * co) % mod;
if (l mid) {
modify(rs, mid + 1, r, lr, rr);
}
t[u] = t[ls] + t[rs];
}
void Modify(int x, int y) {
while (tp[x] != tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
modify(1, 1, n, dfn[x], dfn[y]);
}
ll query(int u, int l, int r, int lr, int rr) {
if (lr mid) {
ans += query(rs, mid + 1, r, lr, rr);
}
return ans % mod;
}
ll Query(int x, int y) {
ll ans = 0;
while (tp[x] != tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
ans += query(1, 1, n, dfn[x], dfn[y]);
return ans % mod;
}
int main() {
n = read(), m = read();
for (int i = 2; i () + 1;
e[fa[i]].emplace_back(i);
e[i].emplace_back(fa[i]);
}
for (int i = 1; i (), r = read() + 1, z = read() + 1;
xunwen[i] = ask{i, l, z, 0};
xunwen[i + m] = ask{i, r, z, 1};
}
dep[1] = 1;
dfs(1);
gettop(1, 1);
m >= 1;
for (int i = 1; i P4216 [SCOI2015] 情报传递 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这个题就是树链剖分与树状数组的搭配,由于风险值会随着时间变化,风险值有一个限度,我们可以利用当前时间减去风险值来得到一个时间节点,在这个时间节点之前开始搜集情报的人就会产生威胁。
由于只是对一条链产生威胁,所以可以使用差分,用树状数组来维护。
//The code was written by yifan, and yifan is neutral!!!
#include
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define lowbit(x) (x & (-x))
template
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch '9') {
fg |服务器托管网= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch e[N], tim[N];
void dfs(int u) {
L[u] = ++ tot;
dep[u] = dep[fa[u]] + 1;
siz[u] = 1;
for (int &v : e[u]) {
dfs(v);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) {
son[u] = v;
}
}
R[u] = tot;
}
void gettop(int u, int Top) {
tp[u] = Top;
if (!son[u]) return ;
gettop(son[u], Top);
for (int v : e[u]) {
if (v == son[u]) continue ;
gettop(v, v);
}
}
int Lca(int x, int y) {
while (tp[x] ^ tp[y]) {
if (dep[tp[x]] dep[y]) {
swap(x, y);
}
return x;
}
void modify(int x, int v) {
while (x ();
for (int i = 1; i ();
e[fa[i]].emplace_back(i);
}
for (rt = 1; fa[rt]; rt = fa[rt]);
dfs(rt);
gettop(rt, rt);
q = read();
for (int i = 1; i ();
if (opt[i] == 1) {
X[i] = read(), Y[i] = read();
int c = read();
if (c ();
}
}
for (int i = 1; i 服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: 【Linux】Linux小程序-进度条一、r和n的理解二、行缓冲区概念三、进度条源代码 老铁们,记着点赞加关注!!!
目录 一、r和n的理解 二、行缓冲区概念 三、进度条源代码 一、r和n的理解 r:回车; n:换行; 那么请问这两个有什么区别呢? 比如:我们在编写内容的时候,一行没有写完的情况下,需要换到下一行…

