「学习笔记」Garsia-Wachs 算法

前言
本文的资料和图片均来自 (texttt{OI-Wiki})。

引入

题目描述
在一个操场上摆放着一排 (N) 堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的 (2) 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。
试设计一个算法，计算出将 (N) 堆石子合并成一堆的最小得分。
((N leq 40000))

过程

我们看到这个题，自然而然会想到区间 DP，即朴素的做法。

#include
using namespace std;
typedef long long ll;

ll r[600], g[600];
ll dp[600][600];

int main() {
	int n;
	scanf("%d", &n);
	for (int i = 1; i 

交上去后，你会发现，RE 了 (7) 个。
为什么？
因为 (n) 太大了，二维数组开不下，其次就算是用了什么不为人知的手段开下了这么大的数组，(n^2) 的复杂度也铁定超时。
这可怎么办呢？
下面介绍一种专门处理石子合并这类问题的算法——Garsia-Wachs 算法

Garsia-Wachs 算法

Garsia-Wachs 的步骤如下：
在序列的两端设置极大值。
在序列中找到前三个连续的权重值 (x, y, z) 使得 (x leq z)。因为序列结尾的最大值大于之前的任意两个有限值，所以总是存在这样的三元组。
从序列中移除 (x) 和 (y)，并在原来 (x) 的位置以前大于或等于 (x+y) 且距 (x) 最近的值的右边重新插入元素，元素值为 (x+y)。因为左端最大值的存在，所以总是存在这样的位置。
为了有效地实现这一阶段，该算法可以在任何平衡二叉查找树结构中维护当前值序列。这样的结构允许我们在对数时间内移除 (x) 和 (y)，并重新插入新节点 (x + y)。
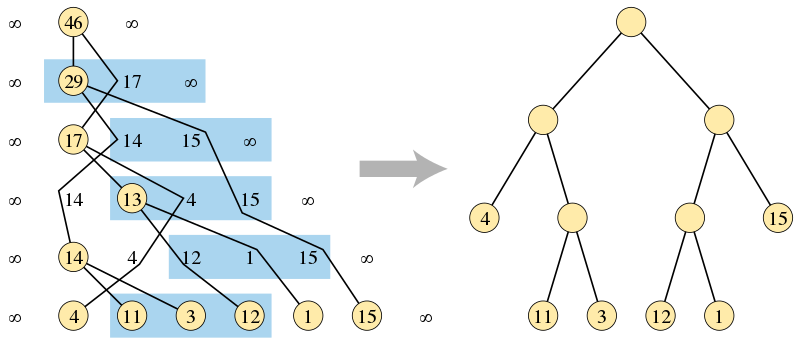
在每一步中，数组中位于偶数索引上直到 (y) 值的权重形成了一个递减序列，位于奇数索引位的权重形成另一个递减序列。因此，重新插入 (x+y) 的位置可以通过在对数时间内对这两个递减序列使用平衡树执行两次二分查找找到。通过从前一个三元组 (z) 值开始的线性顺序搜索，我们可以在总线性时间复杂度内执行对满足 (x leq z) 的第一个位置的搜索。
如果实在不会平衡树，vector 的 insert 和 erase 操作也是个不错的选择呢！

Garsia-Wachs 算法的总时间复杂度为 (O(nlog n))，时间复杂度证明？我只能说，学 OI 记住结论就好了，证明，那是数学要考虑的事，不是 OI 要考虑的事 考试又不会让你证明时间复杂度
至于正确性的证明我也不会= =，这个算法应用范围十分有限，因此学的价值不是很高，“会用” + “知道有这个东西” 就行了
关于上面那道引入题的代码：

#include 
using namespace std;
typedef long long ll;

inline ll read() {
	ll x = 0;
	int fg = 0;
	char ch = getchar();
	while (ch  '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch  g;

int merge() {
	int k = g.size() - 2;
	for (int i = 0; i = 0; -- i) {
		if (g[i] >= tmp) {
			t = i;
			break;
		}
	}
	g.insert(g.begin() + t + 1, tmp);
	return tmp;
}

int main() {
	n = read();
	for (int i = 1; i 

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.fwqtg.net