1 请说一说HashMap实现原理,扩容的条件,链表转红黑树的条件是什么 ?
这道题想考察什么?
1、HashMap的底层原理?
2、HashMap的扩容条件以及链表转换红黑树的条件
考察的知识点
HashMap原理、HashMap扩容条件的理解
考生如何回答
HashMap实现原理
HashMap内部是使用一个默认容量为16的数组来存储数据的,而数组中每一个元素却又是一个链表的头结点,所以,更准确的来说,HashMap内部存储结构是使用哈希表的拉链结构(数组+链表)。
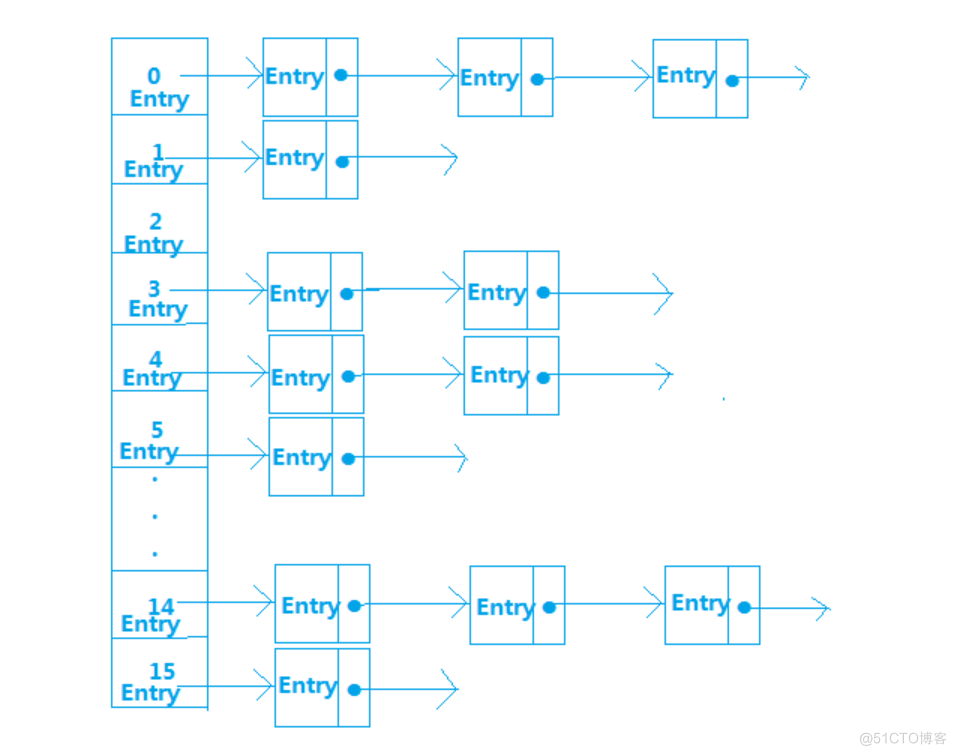
HashMap中默认的存储大小就是一个容量为16的数组,所以当我们创建出一个HashMap对象时,即使里面没有任何元素,也要分别一块内存空间给它,而且,我们再不断的向HashMap里put数据时,当达到一定的容量限制时,Has服务器托管网hMap就会自动扩容。
HashMap扩容条件
HashMap 的实例有两个参数影响其性能:“初始容量” 和 “加载因子”。容量 是哈希表中桶的数量,初始容量 只是哈希表在创建时的容量。加载因子 是哈希表在其容量自动增加之前可以达到多满的一种尺度。当哈希表中的条目数超出了加载因子与当前容量的乘积时,并且要存放的位置已经有元素了(hash碰撞),必须满足这两个条件,才要对该哈希表进行 rehash 操作,会将容量扩大为原来两倍。通常,默认加载因子是 0.75, 这是在时间和空间成本上寻求一种折衷。加载因子过高虽然减少了空间开销,但同时也增加了查询成本。
我们看下HashMap的put函数方法:
public V put(K key, V value) {
if (table == EMPTY_TABLE) {//如果散列表是空的
inflateTable(threshold);//会去建一个表
}
if (key == null) //hashmap会把key为空的放在数组头部
return putForNullKey(value);
int hash = sun.misc.Hashing.singleWordWangJenkinsHash(key);//根据key生成hash值
int i = indexFor(hash, table.length); //生成散列表中的索引,也就是数组下标
for (HashMapEntry e = table[i]; e != null; e = e.next) {//遍历链表,看是否存在key值一样的对象,如果有的话就替换value值
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
//如果没找到key值一样的,就添加
addEntry(hash, key, value, i);
return null;
}如何根据hash值生成数组下标,看indexFor()函数:
static int indexFor(int h, int length) {
// assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";
return h & (length-1);
//为什么长度要是偶数,因为hash值与length的与值不能超过length -1,要不然数组/就越界了,例如hash值是11000111B,length = 1000B,h & (length-1) = 111B,这样得到数组索引肯定不会越界了
}
void resize(int newCapacity) {
HashMapEntry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
HashMapEntry[] newTable = new HashMapEntry[newCapacity];//新建一个数组
transfer(newTable);//完成新旧数组拷贝
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}我们在看看最后的扩容步骤:
void transfer(HashMapEntry[] newTable) {
int newCapacity = newTable.length;
for (HashMapEntry e : table) {//遍历整个数组
while(null != e) {//将同一个位置的元素按链表顺序取出
HashMapEntry next = e.next;//先将当前元素指向的下一个元素存起来,一个一个存放到新表的位置中,记住不一定是同一位置,因为长度变了
int i = indexFor(e.hash, newCapacity);//根据新数组长度,重新生成数组索引
e.next = newTable[i];//将当前位置的元素链表头指向即将新加入的元素,
newTable[i] = e;//然后放入数组中,完成同一位置元素链表的拼接,最先添加的元素总在链表末尾
e = next;//然后继续循环,拿出下一个元素
}
}
}链表转红黑树的条件
首先通过源码来分析下问题:
//用来衡量是否要转红黑树的重要参数
static final int TREEIFY_THRESHOLD = 8;
//转红黑树需要的最小数组长度
static final int MIN_TREEIFY_CAPACITY = 64;
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// TREEIFY_THRESHOLD - 1=7,也就是说一旦binCount=7时就会执行下面的转红黑树代码
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
final void treeifyBin(Node[] tab, int hash) {
int n, index; Node e;
//这里的tab指的是本HashMap中的数组,n为数字长度,如果数组为null或者数组长度小于64
if (tab == null || (n = tab.length) hd = null, tl = null;
do {
TreeNode p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}可以知道【TREEIFY_THRESHOLD – 1】=7,所以binCount=7时才会转红黑树,而binCount初始赋值是0,++count是先加再用,所以其实binCount是从1开始的,1,2,3,4,5,6,7,每一个数值对应的都会创建一个newNode,所以binCount到数值7时,创建了7个新的Node节点,但是情不要忘记,我们创建的节点都是p.next,也就是p的后继节点,所以加上原来的p节点,也可以理解成是链表首节点,7+1=8,就是8个节点,所以链表里元素数目到8个时,会开始转红黑树。
总结:
当链表元素数目到8个,同时HashMap的数组长度要大于64,链表才会转红黑树,否则都是做扩容。
2 请说一说二叉树遍历步骤?
这道题想考察什么?
1、二叉树的基本原理和遍历的方法?
考察的知识点
二叉树遍历的基本流量、二叉树的基本原理
考生如何回答
二叉树的基本概念
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树的性质
二叉树具有以下几个性质:
- 二叉树中,第 i 层最多有 2i-1 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
二叉树的遍历
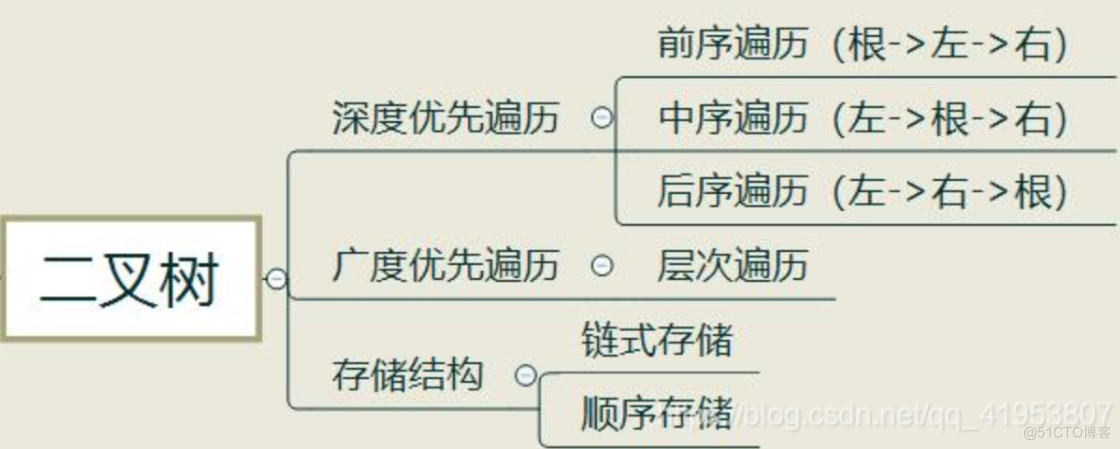
二叉树的遍历方式主要有:先序遍历、中序遍历、后序遍历、层次遍历。先序、中序、后序其实指的是父节点被访问的次序。若在遍历过程中,父节点先于它的子节点被访问,就是先序遍历;父节点被访问的次序位于左右孩子节点之间,就是中序遍历;访问完左右孩子节点之后再访问父节点,就是后序遍历。不论是先序遍历、中序遍历还是后序遍历,左右孩子节点的相对访问次序是不变的,总是先访问左孩子节点,再访问右孩子节点。而层次遍历,就是按照从上到下、从左向右的顺序访问二叉树的每个节点。
先序遍历
代码如下:
//filename: BinTreeNode.h
template
void travPre_R(BinTreeNode * root) {//二叉树先序遍历算法(递归版)
if (!root) return;
cout data;
travPre_R(root->LeftChild);
travPre_R(root->RightChild);
}中服务器托管网序遍历
代码如下:
template
void travIn_R(BinTreeNode * root) {//二叉树先序遍历算法(递归版)
if (!root)
return;
travPre_R(root->LeftChild);
cout data;
travPre_R(root->RightChild);
}3 采用递归和非递归对二叉树进行遍历?
这道题想考察什么?
1、二叉树的基本原理和遍历的方法?
考察的知识点
二叉树遍历的基本概念、二叉树的基本原理
考生如何回答
二叉树的基本概念
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树的遍历
- 前序遍历:每个树的遍历顺序为:根节点→左节点→右节点。上图的前序遍历输出为:FCADBEHGM
- 中序遍历:每个树的遍历顺序为:左节点→根节点→右节点。上图的前序遍历输出为:ACBDFHEMG
- 后序遍历:每个树的遍历顺序为:左节点→右节点→根节点。上图的前序遍历输出为:ABDCHMGEF
前序遍历
递归法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List res = new ArrayList();
public List preorderTraversal(TreeNode root) {
//中 ——> 左 ——> 右
preorder(root);
return res;
}
private void preorder(TreeNode node){
if(node == null) return;
res.add(node.val);
preorder(node.left);
preorder(node.right);
}
}
非递归法:
===基本的算法思想===
创建一个栈,用来储存遍历的轨迹:
1.如果栈不为空则储存当前栈顶元素的值,并弹栈;
2.如果栈顶元素存在右儿子,将右儿子压入;
3.如果栈顶元素有左儿子,将左儿子压入
4.重复1直至栈为空
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List preorderTraversal(TreeNode root) {
List res = new ArrayList();
Stack stack = new Stack();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()){
if(cur != null){
res.add(cur.val);
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
cur = cur.right;
}
}
return res;
}
}中序遍历
递归法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List res = new ArrayList();
public List inorderTraversal(TreeNode root) {
inorder(root);
return res;
}
public void inorder(TreeNode node){
if(node == null) return;
inorder(node.left);
res.add(node.val);
inorder(node.right);
}
}
非递归法:
class Solution {
public List inorderTraversal(TreeNode root) {
List res = new ArrayList();
Stack stack = new Stack();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()){
//压栈
if(cur != null){
stack.push(cur);
cur = cur.left;
}else{
//左边已经存完,弹栈
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
}后序遍历
递归法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List res = new ArrayList();
public List postorderTraversal(TreeNode root) {
//左右中
postorder(root);
return res;
}
private void postorder(TreeNode node){
if(node == null) return;
postorder(node.left);
postorder(node.right);
res.add(node.val);
}
}
非递归法:
基本的算法思想:
使用栈来记录遍历轨迹,并使用一个变量来储存上一次方法的元素,当当前元素左右儿子为空或当前元素已经在上一轮访问过(即上一次方法访问的元素为当前访问元素的节点),则栈顶元素出栈。
class Solution {
public List postorderTraversal(TreeNode root) {
List res = new ArrayList();
if(root == null) return res;
Stack stack = new Stack();
TreeNode pre = null;
stack.push(root);
while(!stack.isEmpty()){
TreeNode cur = stack.peek();
if((cur.left == null && cur.right == null)
|| (pre != null && (cur.right == pre || cur.left == pre))){
res.add(cur.val);
pre = cur;
stack.pop();
}else{
if(cur.right != null) stack.add(cur.right);
if(cur.left != null) stack.add(cur.left);
}
}
return res;
}
}4 对称和非对称加密,MD5的原理?
这道题想考察什么?
1、对称和非对称加密算法的原理?
2、MD5的基本的概念和原理?
考察的知识点
MD5算法原理、对称和非对称加密算法
考生如何回答
对称和非对称加密算法的基本概念
对称加密和非对称加密的基本概念
对称加密指的就是加密和解密使用同一个秘钥,所以叫做对称加密。对称加密只有一个秘钥,作为私钥。常见的对称加密算法:DES,AES,3DES等等。非对称加密指的是:加密和解密使用不同的秘钥,一把作为公开的公钥,另一把作为私钥。公钥加密的信息,只有私钥才能解密。私钥加密的信息,只有公钥才能解密。常见的非对称加密算法:RSA,ECC。
对称加密和分对称加密算法的区别
- 对称加密:加密解密用同一个密钥,被黑客拦截不安全 。
- 非对称加密:公钥加密,私钥解密;公钥可以公开给别人进行加密,私钥永远在自己手里,非常安全,黑客拦截也没用,因为私钥未公开。
指加密和解密使用不同密钥的加密算法,也称为公私钥加密。假设两个用户要加密交换数据,双方交换公钥,使用时一方用对方的公钥加密,另一方即可用自己的私钥解密。常见的非对称加密算法:RSA、DSA(数字签名用)、ECC(移动设备用)、Diffie-Hellman、El Gamal。
- RSA:由 RSA 公司发明,是一个支持变长密钥的公共密钥算法,需要加密的文件块的长度也是可变的。
- DSA(Digital Signature Algorithm):数字签名算法,是一种标准的 DSS(数字签名标准
-
ECC(Elliptic Curves Cryptography):椭圆曲线密码编码学。
ECC和RSA相比,在许多方面都有对绝对的优势,主要体现在以下方面:
(1)抗攻击性强。相同的密钥长度,其抗攻击性要强很多倍。
(2)计算量小,处理速度快。ECC总的速度比RSA、DSA要快得多。
(3)存储空间占用小。ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多,意味着它所占的存贮空间要小得多。这对于加密算法在IC卡上的应用具有特别重要的意义。
(4)带宽要求低。当对长消息进行加解密时,三类密码系统有相同的带宽要求,但应用于短消息时ECC带宽要求却低得多。带宽要求低使ECC在无线网络领域具有广泛的应用前景。
5 对称加密和分对称加密算法的区别
MD5的基本概念
MD5加密
MD5本身是一个128位的0/1比特。一般被表示为16进制的字符串。4个比特位组成一个16进制字符,因此常常能见到的是(128/4=)32个16进制字符组成的字符串 4951 dd1c bff8 cbbe 4cd4 475c a939 fc8b,当然它实质是一种消息摘要算法。
MD5加密的特点:
- 不可逆运算
- 对不同的数据加密的结果是定长的32位字符(不管文件多大都一样)
- 对相同的数据加密,得到的结果是一样的(也就是复制)。
- 抗修改性 : 信息“指纹”,对原数据进行任何改动,哪怕只修改一个字节,所得到的 MD5 值都有很大区别.
- 弱抗碰撞 : 已知原数据和其 MD5 值,想找到一个具有相同 MD5 值的数据(即伪造数据)是非常困难的.
- 强抗碰撞: 想找到两个不同数据,使他们具有相同的 MD5 值,是非常困难的
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net

