5 算法层面
代价敏感:设置损失函数的权重,使得少数类判别错误的损失大于多数类判别错误的损失;
单类分类器方法:仅对少数类进行训练,例如运用SVM算法;
集成学习方法:即多个分类器,然后利用投票或者组合得到结果。
6 代价敏感算法
6.1 相关问题
经典分类方法一般假设各个类别的错分代价是相同的,并且以全局错分率最低为优化目标。
以入侵检测为例,“将入侵行为判别为正常行为的代价”与“将正常行为判别为入侵行为的代价”是不同的,前者会引起安全问题,后者只是影响了正常行为。
基于代价敏感学习分类方法以分类错误总代价最低为优化目标,能更加关注错误代价较高类别的样本,使得分类性能更加合理。
实现方法:
- 改变原始的数据分布来得到代价敏感的模型;
- 对分类的结果进行调整,以达到最小损失的目的;
- 直接构造一个代价敏感的学习模型。
代价矩阵:

- 错误分类造成的代价要大于正确分类所需要的代价,即
C
10
>
C
11
C_{10} > C_{11}
C10>C11、C
01
>
C
00
C_{01} > C_{00}
C01>C00,通常情况下,可以设置C
11
=
C
00
=
0
C_{11} = C_{00} = 0
C11=C00=0,C
10
C_{10}
C10和C
01
C_{01}
C01设置一个大于0的值; - 在非平衡分类的代价敏感学习中,为了提高少数类样本的识别准确率,少数类的错分代价应当大于多数类的错分代价,假设这里的正类(1)是少数类,负类(0)是多数类,那么要求
C
10
>
C
01
C_{10} > C_{01}
C10>C01。
6.2 MetaCost算法(bagging)
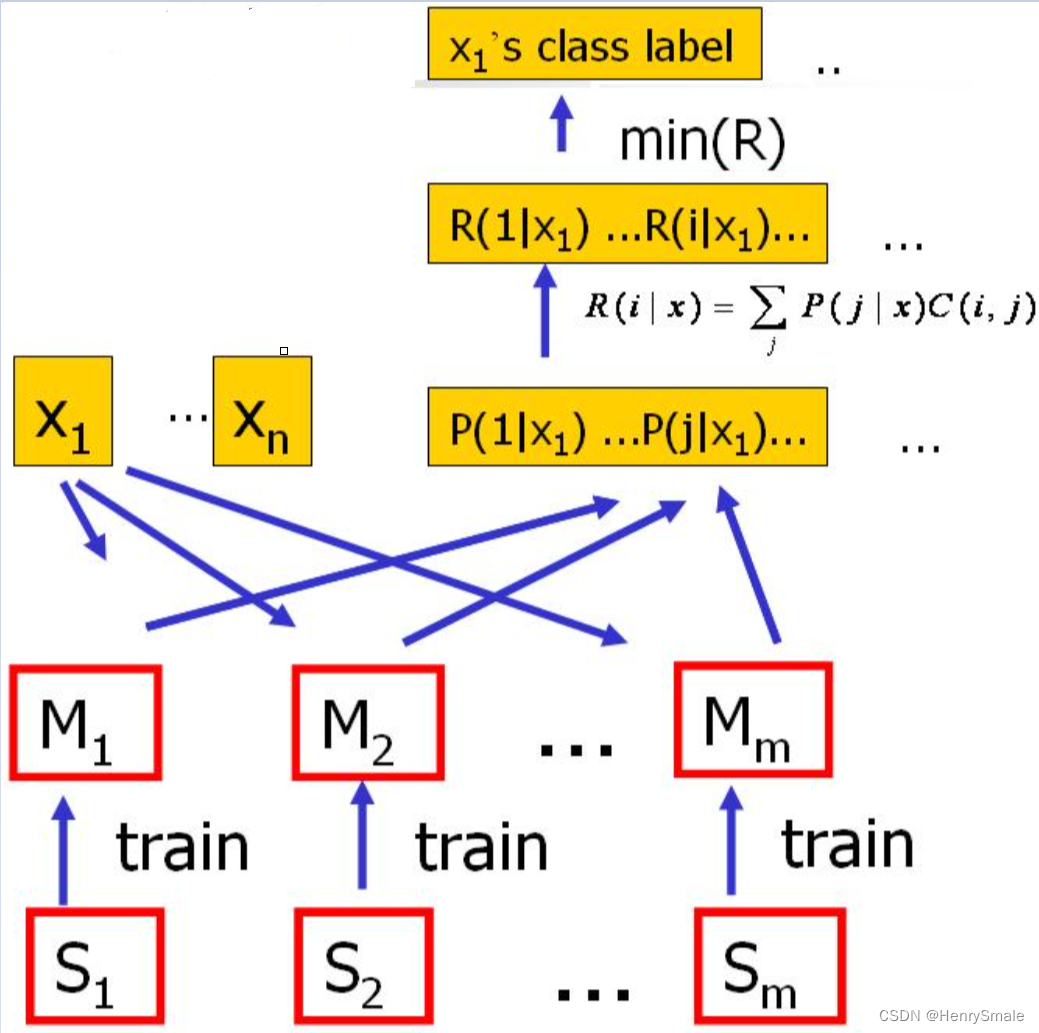
具体步骤如下:
- 对原始训练集进行
m
m
m次随机采样得到m
m
m个子数据集; - 对每一个子数据集训练一个基分类器,得到
m
m
m个基分类器; - 所有基分类器对原始数据进行预测,将所有预测概率值进行平均;
- 参数
q
q
q如果设置为True,则所有模型都直接预测所有数据,如果设置为False,只预测自己的训练数据(也就是第i
i
i个模型对应的第i
i
i个子数据集); - 样本的预测概率乘上代价敏感矩阵,然后取其中损失最小的类别作为这个样本的新标签。

对于二分类问题,标签为[0 1], 假设样本A的预测概率的均值为[0,8 0.2], 代价敏感矩阵设置为:
[
0
1
5
0
]
left[begin{array}{ll} 0 & 1 5 & 0 end{array}right]
[0510]
其中1对应的是大类样本分错的损失,5表示少数类样本分错的损失。
[
0.8
0.2
]
[
0
1
5
0
]
=
[
1
0.8
]
left[begin{array}{ll}0.8 & 0.2end{array}right] timesleft[begin{array}{ll} 0 & 1 5 & 0 end{array}right] = left[begin{array}{ll}1 & 0.8end{array}right]
[0.80.2][0510]=[10.8]
此时最小值为0.8,我们将这个样本的标签改为0.8所对应的类别 “1”。
6.3 代价敏感SVM
对SVM进行代价敏感学习改造的关键在于其惩罚因子
C
C
C,该参数的作用是表征每个样本在分类器构造过程中的重要程度。如果分类器认为某个样本对于其分类性能很重要,那么可以设置较大的值;反之,就设置较小的值。一般情况下,
C
C
C的值不能太大,也不能太小。根据这个原理,对于不平衡分类而言,少数类样本应当具有更大的惩罚值,表示这些样本在决定分类器参数时很重要。因此,应用于非平衡数据分类,对SVM的最简单、最常见的扩展就是根据每个类别的重要性用
C
C
C值进行加权。权重的值可以根据类之间的不平衡比或单个实例复杂性因素来给出。
对于一个给定的训练数据集
(
(
x
1
,
y
1
,
)
,
…
,
(
x
n
,
y
n
)
)
((x_1,y_1,),…,(x_n,y_n))
((x1,y1,),…,(xn,yn)),标准的非代价敏感支持向量机学习出一个决策边界:
f
(
x
)
=
w
T
(
x
)
+
b
f(x)=w^{T} phi(x)+b
f(x)=wT(x)+b
其中
phi
表示一个映射函数,将样本的特征空间映射到一个更高维的空间,甚至是无限维的空间。参数
w
w
w和
b
b
b的优化目标为:
min
w
,
b
,
1
2
∥
w
∥
2
+
C
∑
i
i
s.t.
y
i
(
w
T
x
i
+
b
)
≥
1
−
i
begin{array}{cl} min _{w, b, xi} & frac{1}{2}|w|^{2}+C sum_{i} xi_{i} text { s.t. } & y_{i}left(w^{T} x_{i}+bright) geq 1-xi_{i} end{array}
minw,b,s.t.21∥w∥2+C∑iiyi(wTxi+b)≥1−i
最小化目标函数中包括两部分,即正则项和损失函数项。标准的支持向量机最小化一个对称的损失函数,称为合页损失函数。
在标准SVM上实现代价敏感有两种方法,分别是偏置惩罚支持向量机(BP-SVM)和代价敏感合页损失支持向量机。
(1)偏置惩罚支持向量机(BP-SVM):
min
w
,
b
,
1
2
∥
w
∥
2
+
C
[
C
+
∑
i
∈
S
+
i
+
C
−
∑
i
∈
S
−
i
]
s.t.
y
i
(
w
T
x
i
+
b
)
≥
1
−
i
begin{array}{ll} min _{w, b, xi} & frac{1}{2}|w|^2+Cleft[C_{+} sum_{i in S_{+}} xi_i+C_{-} sum_{i in S_{-}} xi_iright] text { s.t. } & y_ileft(w^T x_i+bright) geq 1-xi_i end{array}
minw,b,s.t.21∥w∥2+C[C+∑i∈S+i+C−∑i∈S−i]yi(wTxi+b)≥1−i
引入了针对阳性和阴性样本的松弛变量
C
+
C_{+}
C+和
C
−
C_{-}
C−,用来处理假阳性和假阴性不同的误分类代价。
缺点:BP-SVM在训练稀疏数据时,会加大惩罚参数
C
C
C,
C
C
C非常大时,BP-SVM将退化为标准SVM。
(2)代价敏感合页损失支持向量机(CSHL-SVM),可以避免BP-SVM在训练稀疏数据时的缺点:
min
w
,
b
,
1
2
∥
w
∥
2
+
C
[
∑
i
∈
S
+
i
+
服务器托管网 ∑
i
∈
S
−
i
]
s.t.
y
i
(
w
T
x
i
+
b
)
≥
1
−
i
,
i
∈
S
+
y
i
(
w
T
x
i
+
b
)
≥
k
−
i
,
i
∈
S
−
begin{array}{ll} min _{w, b, xi} & frac{1}{2}|w|^2+Cleft[beta sum_{i in S_{+}} xi_i+gamma sum_{i in S_{-}} xi_iright] text { s.t. } & y_ileft(w^T x_i+bright) geq 1-xi_i, quad i in S_{+} & y_ileft(w^T x_i+bright) geq k-xi_i, quad i in S_{-} end{array}
minw,b,s.t.21∥w∥2+C[∑i∈S+i+∑i∈S−i]yi(wTxi+b)≥1−i,i∈S+yi(wTxi+b)≥k−i,i∈S−
其中
=
C
+
,
=
2
C
−
−
1
,
k
=
1
2
C
−
−
1
beta = C_{+}, gamma = 2C_{-} -1, k = frac{1}{2C_{-} -1}
=C+,=2C−−1,k=2C−−11。在CSHL-SVM中,代价敏感由参数
,
,
k
beta, gamma, k
,,k控制,
,
beta, gamma
,可以控制边界违反的相对权重,在稀疏的训练数据集上,
k
k
k依然可以控制代价敏感性。
7 单分类器方法
密度估计法
基于聚类的方法
基于支持域的方法
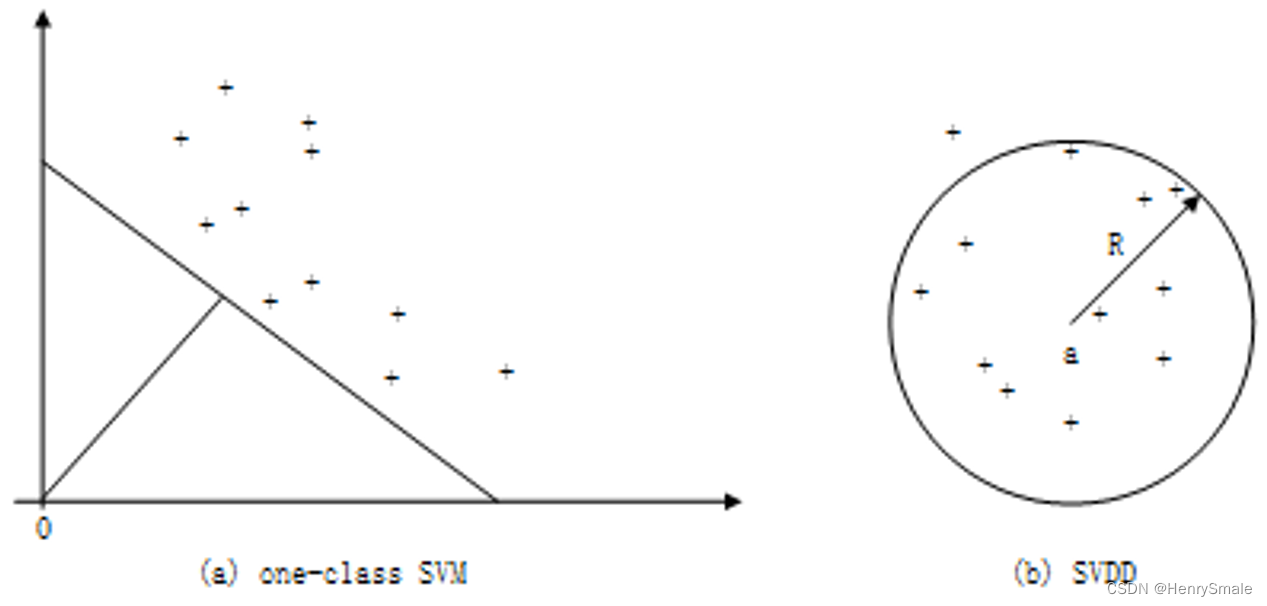
7.1 SVM
单类支持向量机(OneclassSVM)
支持向量数据描述(Support Vector Data Description,SVDD)
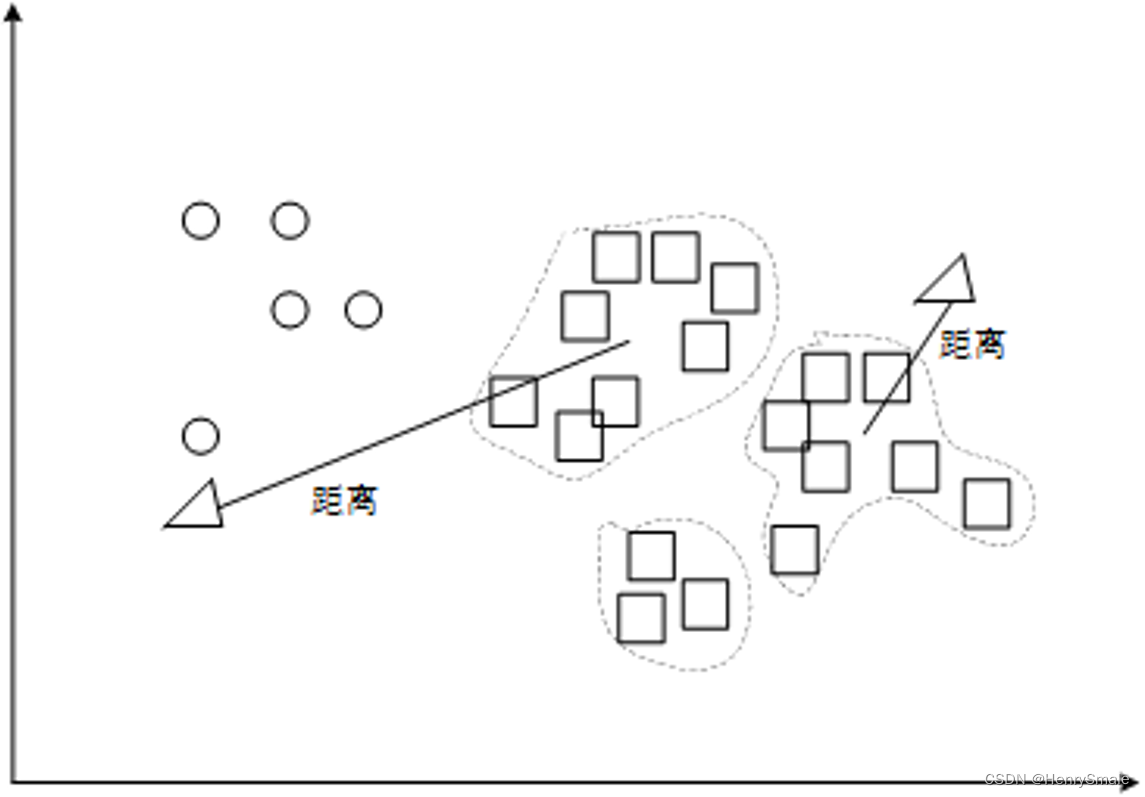
当多数类中存在明显簇结构时,使用聚类方法获得聚类结构有利于提高多数类轮廓描述的精度。
8 集成学习的方法
典型的集成学习方法有
- Bagging
- Boosting
- Stacking
- SMOTEBagging
- SMOTEBoost
8.1 Bagging
Over Bagging:每次迭代时应用随机过采样在小类数据
Under Bagging:每次迭代时应用随机下采样在大类数据
SMOTEBagging:结合了SMOTE与bagging,先使用SMOTE生成更加全面的小类数据,然后应用bagging
Asymmetric bagging:每次迭代时,全部小类数据保留,从大类数据中分离一个与小类数据一样大的子集
8.2 Boosting
SMOTEBoost : 结合了SMOTE方法代替简单的增加小类观察点的权重
BalanceCascade : 是典型的双重集成算法,采用Bagging作为基本的集成学习方法,并在训练每个Boostrap数据时,使用AdaBoost作为分类算法。
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
相关推荐: 通过Python封装接口商品ID获取京东商品历史价格数据,京东历史价格数据,京东API接口
京东商品历史价格数据展示了该商品在一段时间内的价格变化情况,可作为购物决策的重要参考因素。用户可以根据历史价格数据来判断当前商品的价格是否处于一个合理水平,并对接下来的价格趋势进行预测。 京东商品历史价格数据可以在商品详情页面中查看,也可以通过接口获取。对于接…

