目录
1 神经元
2 MP模型
3 激活函数
3.1 激活函数
3.2 激活函数作用
3.3 激活函数有多种
4、神经网络模型
5、神经网络应用
6、存在的问题及解决方案
6.1 存在问题
6.2 解决方案-反向传播
1 神经元
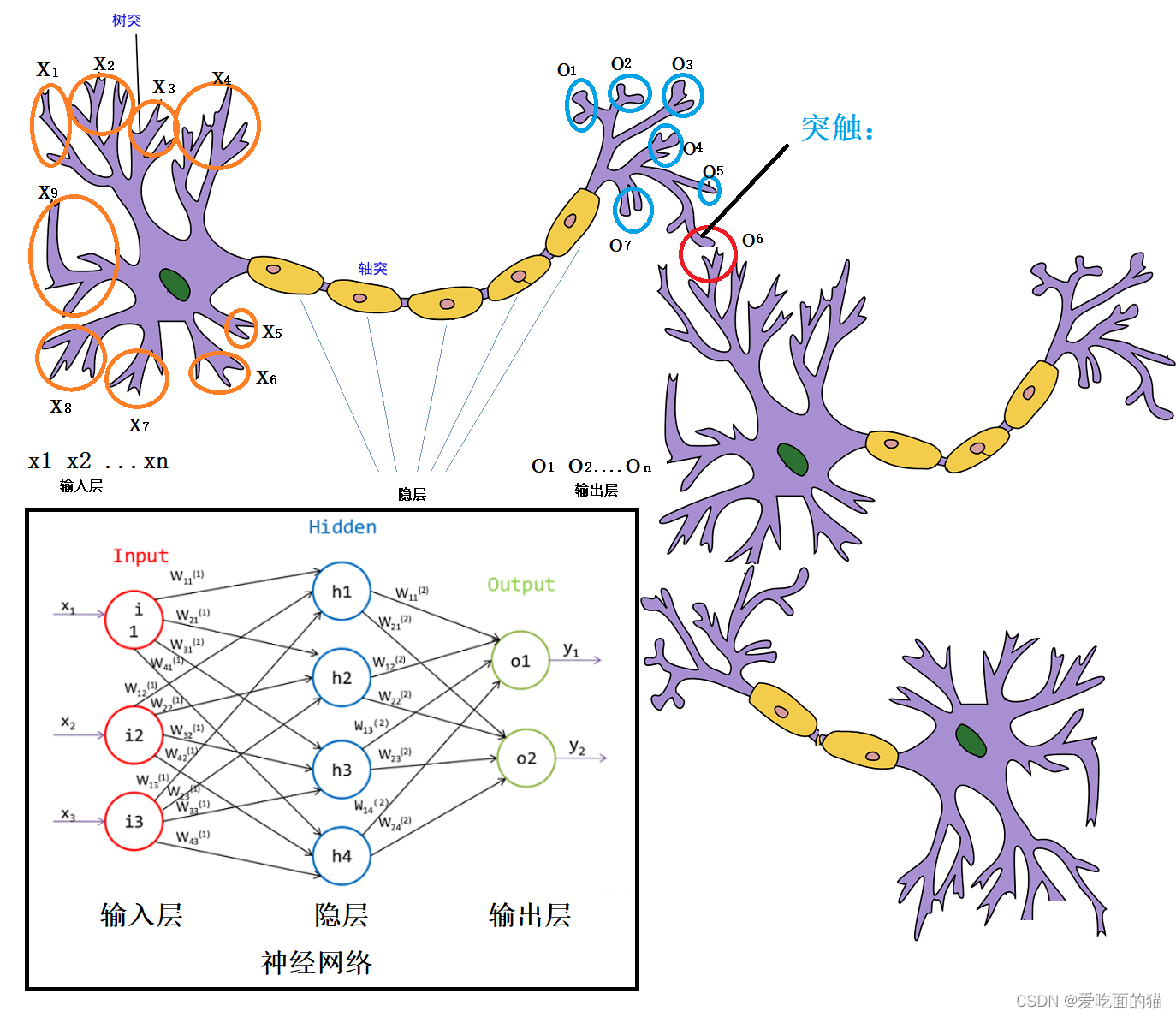
神经元是主要由树突、轴突、突出组成,树突是从上面接收很多信号,经过轴突处理后传递给突触,突触会进行选择性向下一级的树突传递信号。突触输出的信号只有两种可能,要么输出,要么不输出,即只有0和1两种情况。
在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”,那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。

下图错误请忽略(留作自用)
2 MP模型
每个神经网络单元抽象出来的数学MP模型如下,也叫感知器,它接收多个输入(x1,x2,x3…),产生一个输出 即 y= W1X1+W2X2+W3X3+…+WnXn + b。
这就好比是神经末梢感受各种外部环境的变化(感知外部刺激),产生不同的电信号(也就是输入:x1,x2,x3…xn),这些强度不同(也就是参数w1,w2,w3…wn)的电信号汇聚到一起,会改变这些神经元内的电位,如果神经元的电位超过了一个“阈值”(参数 b),它就会被激活(激活函数),即“兴奋”起来,向其他神经元发送化学物质。
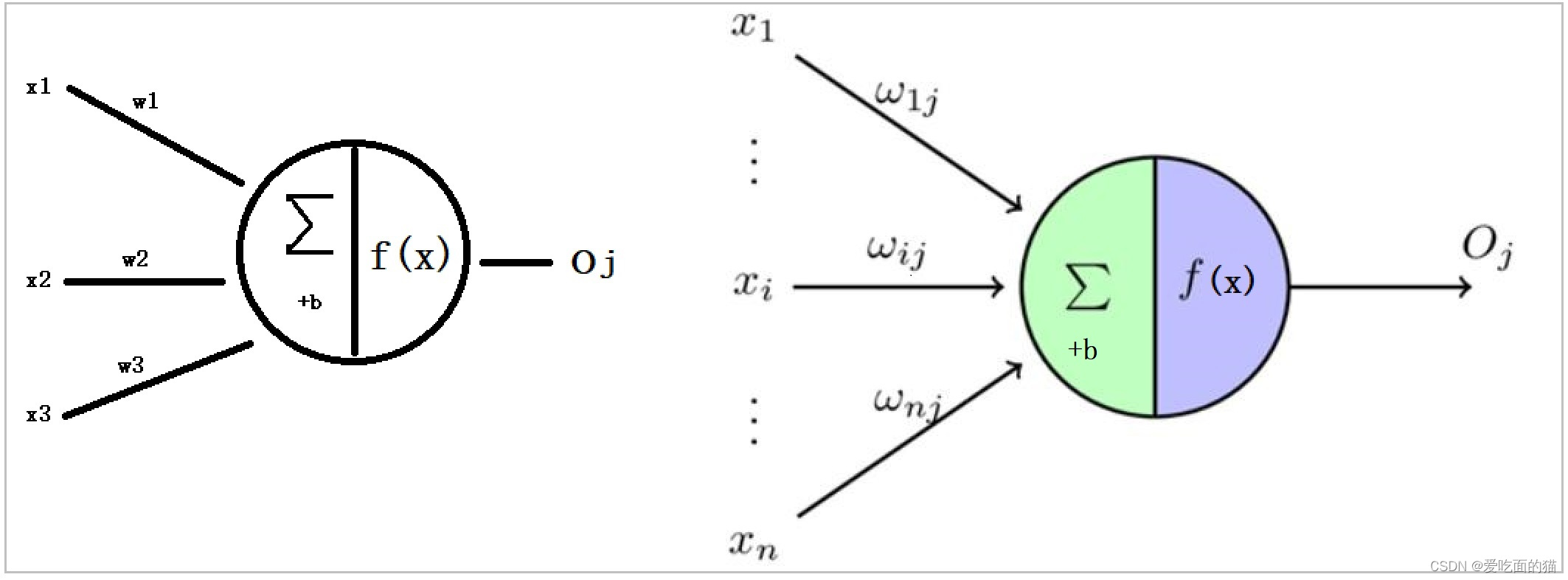
MP模型:麦卡洛克一皮茨模型(McCulloch-Pitts model )简称,一种早期的神经元网络模型.
由美国神经生理学家麦卡洛克(McCulloch, W.)和数学家皮茨 B是第i个神经元的阂值,W是神经元i与神经元J 之间的连结强度。
MP模型过程:
- 每个神经元都是一个多输入端
- 如x1,x2,x3
- 每个输入都会乘以权重w1,w2,w3
- 再加一个阈值 b
- 最后我们会得到 y = w1x1 + w2x2 + w3x3 + b
- 最终我们得到一个值 y
- 得到这个值后是否会向下游输出则取决于激活函数f(x)
- 向下游输出的结果Oj的值要么是0,要么是1。
3 激活函数
3.1 激活函数
就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
3.2 激活函数作用
如果不用激活函数:每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用激活函数:激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
3.3 激活函数有多种
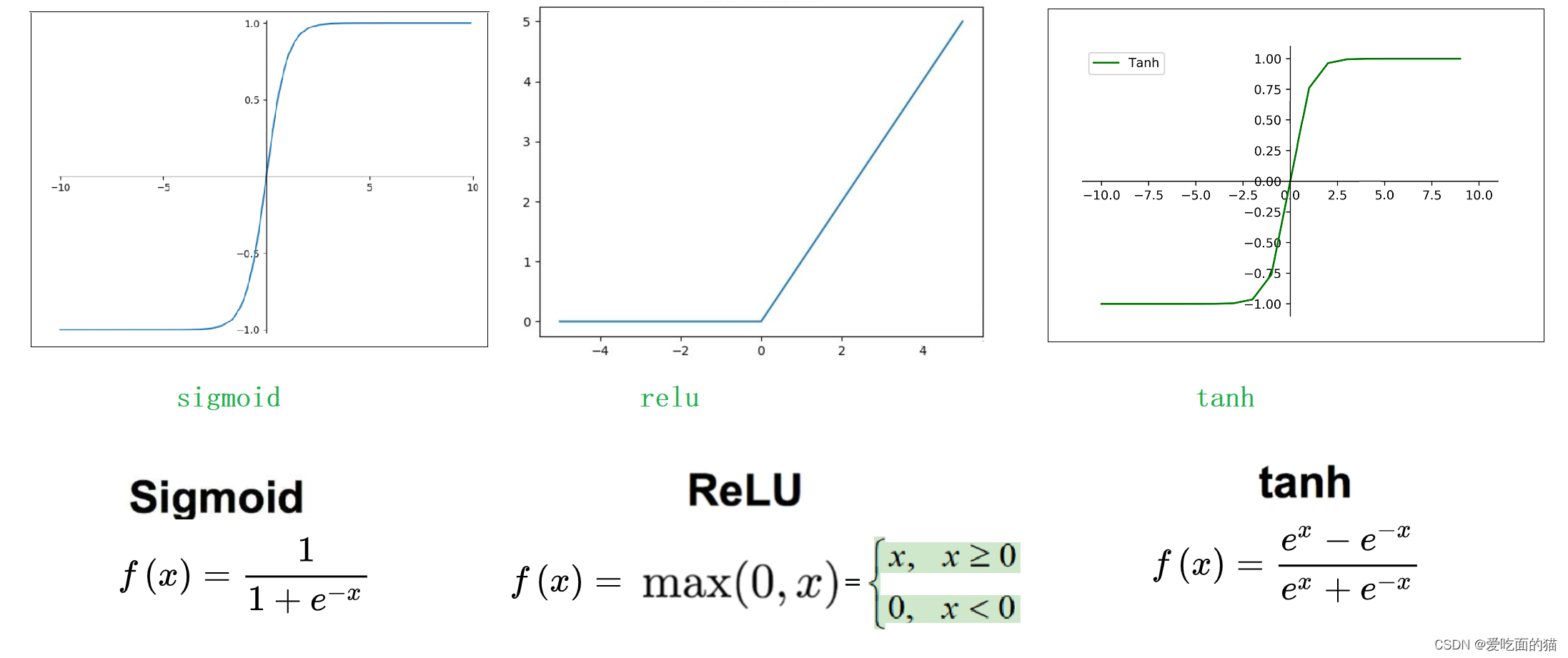
- Sigmoid激活函数
Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。在信息科学中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的阈值函数,将变量映射到0,1之间 。
- ReLU函数
Relu激活函数(The Rectified Linear Unit),用于隐层神经元输出。
- Tanh函数
Tanh是双曲函数中的一个,Tanh()为双曲正切。在数学中,双曲正切“Tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。
4、神经网络模型
单个的感知器(也叫单感知机)就构成了一个简单的模型(MP模型),但在现实世界中,实际的决策模型则要复杂得多,往往是由多个感知器组成的多层网络,如下图所示,这也是经典的神经网络模型(也叫多感知机,也叫人工神经网络),由输入层、隐含层、输出层构成。
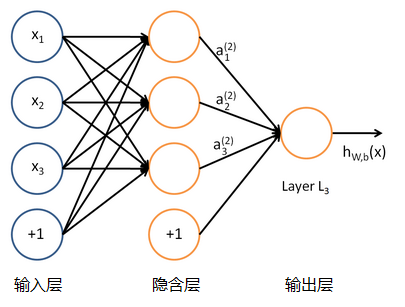
人工神经网络可以映射任意复杂的非线性关系,具有很强的鲁棒性、记忆能力、自学习等能力,在分类、预测、模式识别等方面有着广泛的应用。
5、神经网络应用
神经网络如何帮助我们做一些事情呢?例如语音如何识别?例如图片如何识别?
其本质上都是可以转换为数字,将转换后的数字通过神经网络进行操作。
例如下图,图像显示的是字母X,是一个单通道的5×5=25个像素的黑白图像(像素值只有0和255)。它代表的就是一堆数字(x1,x2,…,x25)=(0,255,255,0,….225,0),这堆数字就是代字母表X。
我们就是通过训练,找到一堆参数,来判断它是不是一个字母X。
目前我们判断图片是不是x,只是通过一层的1个神经元(一个神经元MP模型)就可以判断。
当然,这个1层单个神经元需要的找到的参数是25个参数(W1,W2,W3,…,W25)。
如果是 彩色图像,就是3通道 5*5*3 个像素,1层单个神经元需要的找到的参数就是75个参数(W1,W2,W3,…,W75)。

所以,从本质上讲,无论什么图,本质上都是一堆数字,我们就是把这些数字输入到神经元中进行训练参数,直到找到一个误差最小的函数,这就是成功的训练。
但在现实世界中,实际的决策模型则要复杂得多,例如阅读文章、语音识别、图像识别等,仅仅用一层神经元很难达到效果。于是就需要使用多层神经元,就是多层神经网络模型。
首先先有一个输入,输入端连接第一隐层的每一个神经元,第一隐把这些数据输出后,选择向下游输出到第二隐层,第二隐层输出结果输出到第三隐层。这就是所谓的多层神经网络。
每两层的神经网络连接都会有大量的参数,通过一定的算法,能让大量的参数调节到最优,使得最后的误差函数最小,这样就是一个成功的训练。
6、存在的问题及解决方案
6.1 存在问题
我上面可以说是使用一层单个神经元训练需要找到(单通道)25个或(3通道)75个参数,使用的是全连接方式 y=W1X1+W2X2+W3X3+…+W25X25+b 或y=W1X1+W2X2+W3X3+…+W25X75+b ,但全连接网络存储在最大问题就是太复杂。
例如 有 5×5 图片,有三层神经网路,每个神经网络层有25个神经元。
25个像素(x1,x2,…,x25)作为输入,
输入到第1层第1个神经元需要确定25个参数
输入到第1层第2个神经元需要确定25个参数
….
输入到第1层第25个神经元需要确定25个参数
因此(x1,x2,…,x25)输入到第1层25个神经元需要参数 25 *25 = 625
第1层25个神经元的输出结果又是新的输入(x1,x2,…,x25)
同理,(x1,x2,…,x25)输入到第2层25个神经元需要参数 25 *25 = 625
同理,(x1,x2,…,x25)输入到第3层25个神经元需要参数 25 *25 = 625
因此3层神经网络就需要 625 * 3 = 1875 个 参数需要调。
这还是在 5×5 最简单的图片神经网络才3层的情况下,如果图片是彩色的呢?如果图片是1个比较的图片(3000×1000)呢?如果是彩色大图且网络层数更多如10层呢?
此时的参数量就是 3000×1000 x 3000×1000 x 10 = 300000000000 。这时候识别起来就会更复杂,计算也比较慢。
这也是前几次人工智能陷入低谷的原因。因为不管是算力还是算法,都跟不上。
6.2 解决方案-反向传播
正因为存在上述问题,所以采用辛顿提出的反向传播算法,即BP算法。
BP算法在调整参数时候,不用向以前一样调参,可以先调最后一层,调完最后一层往前调,最后调到最前面一层。这种算法就叫反向传播。这种算法比以前算法复杂度要低得多。所以 反向传播算法 也引领了第三次人工直智能的浪潮。
到这里初步有了对人工智能的粗浅的认识。
7 反向传播
见 人工智能反向传播
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
相关推荐: python推荐系统实现(矩阵分解来协同过滤)|附代码数据
原文链接:http://tecdat.cn/?p=10911 最近我们被客户要求撰写关于推荐系统的研究报告,包括一些图形和统计输出。 用户和产品的潜在特征编写推荐系统矩阵分解工作原理使用潜在表征来找到类似的产品 1. 用户和产品的潜在特征 我们可以通过为每个用…

