03.数组中的重复数字
题目描述:在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。示例 1:输入:[2, 3, 1, 0, 2, 5, 3] 输出:2 或 3 。
思路一:排序
先对原数组进行排序,再在排序的数组中遍历,判断num[n]和nums[n+1]是否相等,如果相等就直接输出。这种思路比较简单,代码如下:
class Solution {
public int findRepeatNumber(int[] nums) {
Arrays.sort(nums);
for(int i=0;i复杂度分析:
- 时间复杂度:数组排序时间复杂度为O(nlogn),数组遍历时间复杂度为O(n),总的时间复杂度为O(nlogn)。
- 空间复杂度:没有引入额外的存储,因此空间复杂度为O(1)。
思路二:哈希
引入一个哈希表,顺序遍历数组,以数组元素值为key,如果key不存在就加入哈希表,如果key存在就直接输出,代码如下:
class Solution {
public int findRepeatNumber(int[] nums) {
HashMap hashMap = new HashMap();
int result = -1;
for(int i=0;i 复杂度分析:
- 时间复杂度:对数组做一次遍历,时间复杂度为O(n)。
- 空间复杂度:使用了一个Hash表的额外存储,空间复杂度为O(n)。
相比思路一,时间复杂度提升了,但是引入了额外的空间复杂度。
思路三:移动
上面两种思路比较通用,对于任何大小的数据都能适用,但是没有利用一个关键的信息:所有数字都在0~n-1的范围内。如果一个长度为n的数组没有重复,且所有数字都在0~n-1的范围内,其排序后的元素值与数组下标一定是一一对应的。如果此时加入了一个重复元素,就会存在一个元素下标i等于其值x,另一个下标j的值也等于x的情况。我们的思路是,对于一个给定的数组,从第一个元素开始,做以下操作:
- 判断下标i和元素nums[i]=x是否相等,如果相等就跳过(i++);不等就判断nums[x]是否等于x,如果相等就说明找到重复数据了,否则:将i和x两个位置的元素交换位置,再进行判断,重复这个过程,直到满足nums[i]=x的条件。
以[2, 3, 1, 0, 2, 5, 3]为例,执行流程如下:
代码如下:
class Solution {
public int findRepeatNumber(int[] nums) {
for(int i=0;i复杂度分析:
- 时间复杂度:代码中虽然有两重循环,但是每个数字最多交换两次就能找到属于他自己的位置,因此总的时间复杂度为O(n)。
- 空间复杂度:没有引入额外的存储,因此空间复杂度为O(1)。
04.二维数组中的查找
题目描述:在一个 n * m 的二维数组中,每一行都按照从左到右 非递减 的顺序排序,每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。示例数组:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
思路:这道题目主要是找规律,跳出固定思维,找到利于计算机迭代计算的方法。需要关注运算的起点,如果这个起点在左上角或者右下角,那么横向或者纵向移动数字的变化趋势是一样的,这就很难定位到应该往哪个方向移动可能会定位到目标数字。而换个思路,从左下角(或者右上角)出发,向上的数字总是变小的,向右的数字总是变大的,这就很容易定位到目标数字的位置。实现上也比较简单,注意细节即可,代码如下:
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
if(matrix == null || matrix.length == 0) {
return false;
}
//定义起始位置为左下角
int i = matrix.length - 1;
int j = 0;
while(i >= 0 && j 05.替换空格
请实现一个函数,把字符串 s 中的每个空格替换成”%20″。示例:输入:s = “We are happy.” 输出:“We%20are%20happy.”
这里需要注意一个点,如果字符串是可变的,且不要求原地替换,那么新建一个字符串,顺序把相应的字符赋值即可。但是一般会要求在原字符串上操作以增加难度,以下都是基于这个限制条件的思路。
思路一:顺序替换
顺序遍历字符串,将空格替换为20%,这是最直观的解法。但是这里面涉及到一个问题:一个字符替换为三个字符,每次遇到空格都需要将剩余的字符向后移动2个位置,时间复杂度为O(n),总的时间复杂度为O(n2)。代码如下(Java字符串本身也是不可变的,需要转换成字符数组操作):
class Solution {
public String replaceSpace(String s) {
if(s == null || s.length() == 0) {
return s;
}
//统计空格个数以确定新字符串的长度
int count = 0;
for (char c : s.toCharArray()) {
if(c == ' ') count++;
}
//创建新的字符数组
char[] chars = new char[s.length() + count * 2];
//初始化字符数组
for (int i = 0; i i + 2 ; j--) {
//往后移动两个位置
chars[j] = chars[j - 2];
}
//替换空格
chars[i] = '%';
chars[i+1] = '2';
chars[i+2] = '0';
}
}
//返回字符串类型
return new String(chars);
}
}思路二:逆序替换
顺序遍历的问题就是每次替换当前字符之后的那些字符都要向后移动,如果换个思路,从后往前遍历,同时维护两个指针:left和right,left指向原始字符串结束位置,right指向替换后字符串的结束位置。从后往前遍历,如果没有遇到空格就依次将chars[left]的值赋给chars[right];遇到空格就填充right、right-1和right-2的位置。从而避免了重复移动,时间复杂度为O(n),代码如下:
class Solution {
public String replaceSpace(String s) {
if(s == null || s.length() == 0) {
return s;
}
//统计数组长度和空格的个数
int n = s.length();
int count = 0;
for(int i=0;i= 0) {
if(arr[left] != ' ') {
arr[right] = arr[left];
left--;
right--;
}else{
arr[right-2] = '%';
arr[right-1] = '2';
arr[right] = '0';
left--;
right -= 3;
}
}
//转换为string输出
return new String(arr);
}
} 06.从尾到头打印链表
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
实现一:栈
单向链表本身是只能从头到尾遍历,这里要求从尾到头,刚好符合栈这个数据结构的特征:依次遍历链表节点压栈,依次弹出返回结果数组。代码如下:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {
if(head == null) return new int[]{};
//入栈并判断栈长度
int size = 0;
Stack stack = new Stack();
while(head != null) {
stack.push(head);
head = head.next;
size++;
}
//弹出并返回数据
int[] res = new int[size];
for(int i=0;i 实现二:递归
链表或者树这种数据结构天然就有递归的特点,且递归本质上也是通过虚拟机函数栈调用实现的。但是递归这种方式比较反人类,需要思考透彻调用逻辑才能写出来正确的代码,核心:1.递归终止条件2.递归返回方式。具体到这个题目,核心逻辑为:添加当前节点之前,先递归下个节点,添加当前节点。另外,需要定义成员变量arraylist,每次遍历到当前节点就追加数据。代码如下:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
List resList = new ArrayList();
public int[] reversePrint(ListNode head) {
if(head == null) {
return new int[0];
}
reverse(head);
//list2array
int[] resArr = new int[resList.size()];
for(int i=0;i 07.重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例:前序{1,2,4,7,3,5,6,8} 中序{4,7,2,1,5,3,8,6}
思路:二叉树的前序和中序遍历能够唯一确定一棵二叉树。这道题目理解起来并不困难,注意两点:1.前序和中序遍历中根节点和左右子树的位置:前序根左右,中序左根右。2.有耐心,一步一步画图理解算法迭代的过程,最终转换成代码实现。核心思想:先在前序里找到根节点,再在中序里找到根节点的位置将中序分成左右两部分,依次迭代。示意图如下: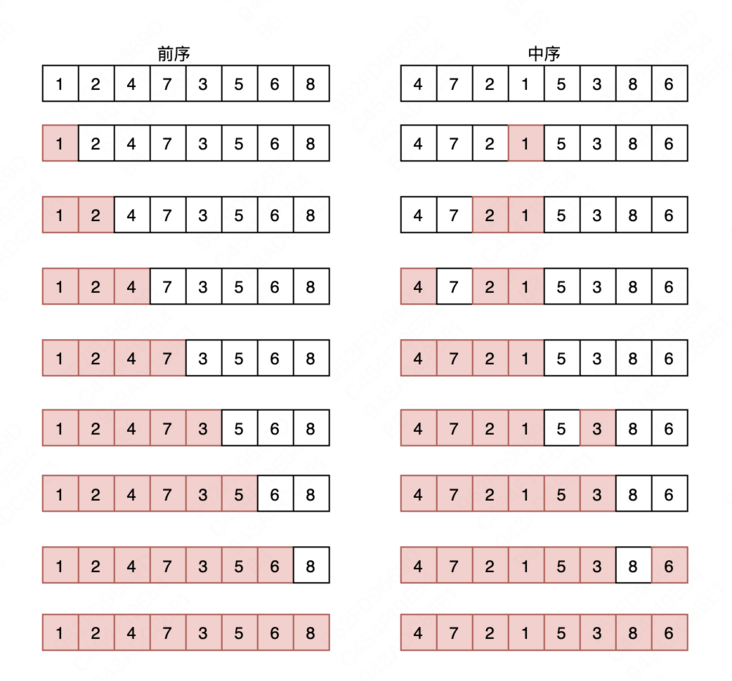
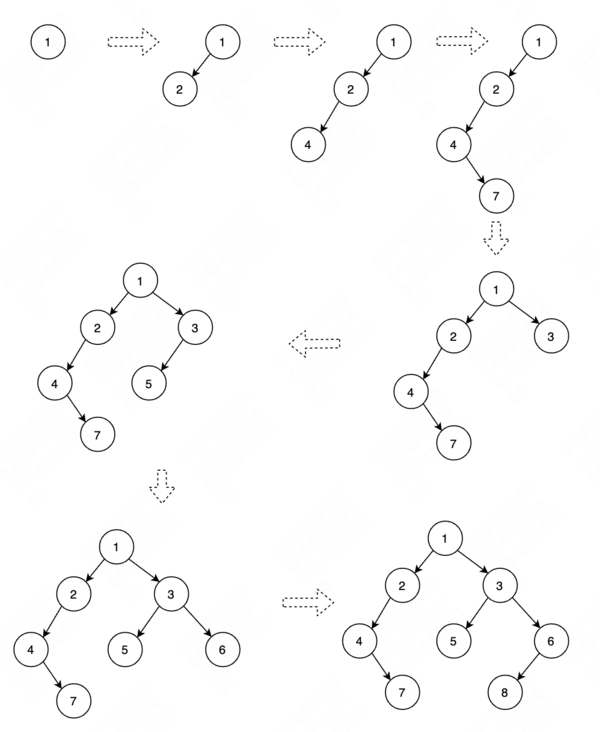
代码实现上需要注意的点:递归。一般来讲树的算法都能用递归实现且代码相对简洁,使用整体思想,考察当前根节点的左右子树的时候将其视为一个整体,不关心其子节点,能够降低理解的复杂度。具体代码如下:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
//HashMap记录中序数组中值和索引的对应关系
public HashMap inMap = new HashMap();
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder == null || preorder.length == 0) {
return null;
}
int n = preorder.length;
//遍历中序构造hashmap
for (int i = 0; i preRight) {
return null;
}
//前序第一个节点为当前子树的根节点
int rootValue = preorder[preLeft];
TreeNode root = new TreeNode(rootValue);
//获取根节点在中序序列中的位置
int rootIndex = inMap.get(rootValue);
//确定左子树的节点数
int leftSize = rootIndex - inLeft;
//确定左右子树
root.left = recurTree(preorder, inorder, preLeft+1, preLeft+leftSize, inLeft, rootIndex-1);
root.right =recurTree(preorder, inorder, preLeft+leftSize+1, preRight, rootIndex+1, inRight);
return root;
}
} 服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net

