之前写过一篇有关TRE优化模型详解的博文：

https://www.cnblogs.com/zoubilin/p/17270435.html

这篇文章里面的附录给出了非线性模型化线性的方式，具体内容如下：

• 首先是篇文章的变量和原模型（具体见我上面那篇笔记）：
  
  
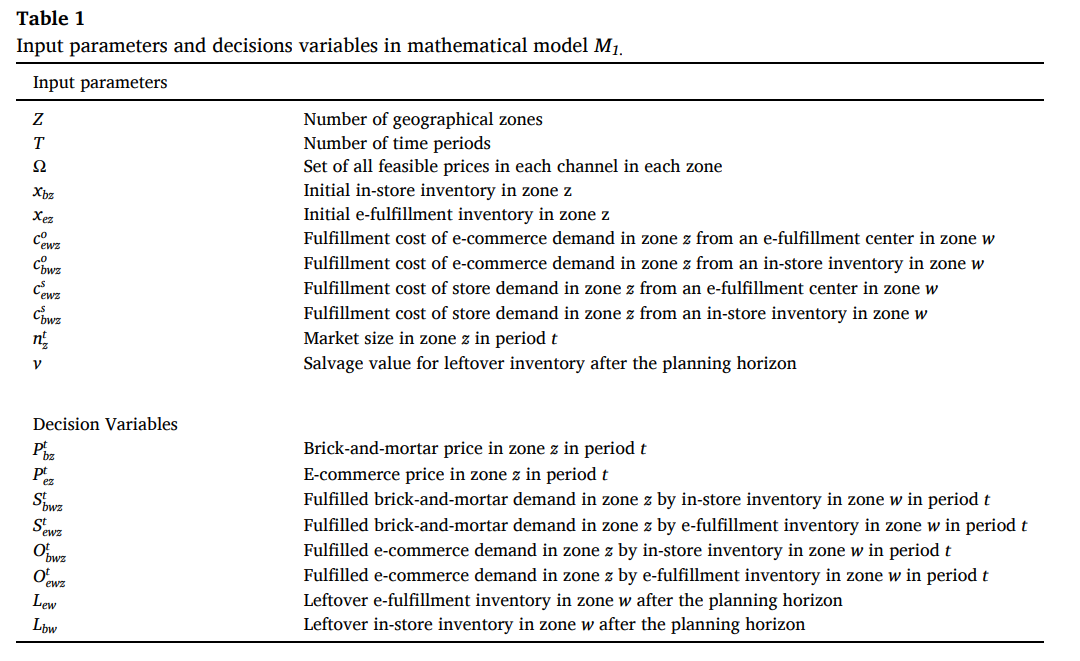
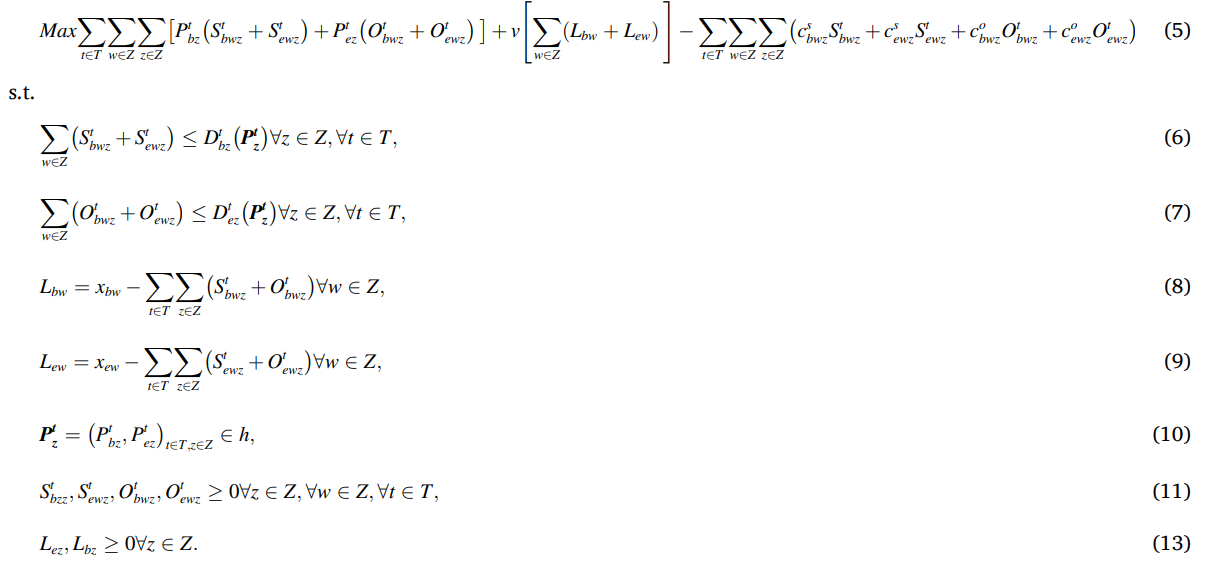
• 其次这篇文章附录给出的非线性化线性的方法：
  
  
  我觉得很经典，所以这几天我废了九牛二虎之力推导了这个附录的公式，并复现了它的化线性的过程•‸ก

一、目标函数

• 目标函数中的非线性项为：

• 引入决策变量：

• 此时应加入下面约束条件，即式(A.13)~式(A.14) 和式(A.28)~式(A.29)：

  [sum_{iin{I_{bzi}^t}}Y^t_{bzi}=1
  ]
  [sum_{iin{I_{ezi}^t}}Y^t_{ezi}=1
  ]
  [Y^t_{bzi},Y^t_{ezi}in{{0,1}}
  ]

• 引入价格集合（已知量），其中(I^t_{bz}、I^t_{ez})为对应渠道的可选择价格数量，(i={1,2,…,I^t_{bz}}或i={1,2,…,I^t_{ez}})：

• 那么有：(P^t_{bz}=sum_{iin{I^t_{bz}}}P^t_{bzi}Y^t_{bzi})、(P^t_{ez}=sum_{iin{I^t_{ez}}}P^t_{ezi}Y^t_{ezi})

• 此时，目标函数变为：

• 目标函数中仍存在非线性项(Y^t_{bzi}sum_{win{Z}}(S^t_{bwz}+S^t_{ewz}))和(Y^t_{ezi}sum_{win{Z}}(O^t_{bwz}+O^t_{ewz}))

  所以需要再引入下面决策变量，也就是式(A.6)~式(A.7)：

  [V^t_{bzi}=Y^t_{bzi}sum_{win{Z}}(S^t_{bwz}+S^t_{ewz})
  ]
  [V^t_{ezi}=Y^t_{ezi}sum_{win{Z}}(O^t_{bwz}+O^t_{ewz})
  ]

  此时目标函数变为下式，也就是式(A.8) 的由来：

设(sum_{win{Z}}(S^t_{bwz}+S^t_{ewz}))的上限为(a)，(sum_{win{Z}}(O^t_{bwz}+O^t_{ewz}))的上限为(b)，要彻底转换目标函数变为线性，需要增加新的约束如下，包含了式(A.15)-式(A.18)、式(A.33)-式(A.34)：

二、约束条件

• 非线性项为(D^t_{bz}(P^t_{z}))和(D^t_{ez}(P^t_{z}))

• 经过上面的转换，有：

  • (e^{beta_{0z}+beta_{1z}P^t_{bz}}=e^{beta_{0z}+beta_{1z}sum_{iin{I^t_{bz}}}(P^t_{bzi}Y^t_{bzi})})其中，(Y^t_{bzi})是一个0-1变量，所以又可以写成：(e^{beta_{0z}+beta_{1z}P^t_{bz}}=sum_{iin{I^t_{bz}}}Y^t_{bzi}e^{beta_{0z}+beta_{1z}P^t_{bzi}}).

  • 同理，(e^{beta_{0z}+beta_{1z}P^t_{ez}}=sum_{iin{I^t_{ez}}}Y^t_{ezi}e^{beta_{0z}+beta_{1z}P^t_{ezi}})

• 令

  [r^t_{bzi}=e^{beta_{0z}+beta_{1z}P^t_{bzi}}
  ]
  [r^t_{ezi}=e^{beta_{0z}+beta_{1z}P^t_{ezi}}
  ]

  即式(A.1)~式(A.2)，那么有：

  [D^t_{bz}(P^t_z)=n^t_zfrac{sum_{iin{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}}{sum_{iin{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+sum_{iin{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}+1}
  ]
  [D^t_{ez}(P^t_z)=n^t_zfrac{sum_{iin{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}}{sum_{iin{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+sum_{iin{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}+1}
  ]

• 为了将(D^t_{bz}(P^t_{z}))和(D^t_{ez}(P^t_{z}))化为线性，令：

  [R^t_z=frac{1}{sum_{iin{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+sum_{iin{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}+1}
  ]

  即式(A.3)。那么(D^t_{bz}(P^t_{z})=n^t_zR^t_zsum_{iin{I^t_{bz}}}Y^t_{bzi}r^t_{bzi})，(D^t_{ez}(P^t_{z})=n^t_zR^t_zsum_{iin{I^t_{ez}}}Y^t_{ezi}r^t_{ezi})，需要明确的是：(sum_{iin{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+sum_{iin{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}geq{0})，故(R^t_zleq{1})

• 此时仍存在非线性项(sum_{iin{I^t_{bz}}}R^t_zY^t_{bzi}r^t_{bzi})和(sum_{iin{I^t_{ez}}}R^t_zY^t_{ezi}r^t_{ezi})

  令：

  [U^t_{bzi}=R^t_zY^t_{bzi}
  ]
  [U^t_{ezi}=R^t_zY^t_{ezi}
  ]

  即式(A.4)-式(A.5)。此时需要新增的约束条件如下，包含了式(A.21)-式(A.27)、式(A.32)-式(A.34)：

  [U^t_{bzi},U^t_{ezi}geq{0}
  ]
  [R^t_zgeq{0}
  ]
  [U^t_{bzi}leq{Y^t_{bzi}}
  ]
  [U^t_{ezi}leq{Y^t_{ezi}}
  ]
  [U^t_{bzi}leq{R^t_z}
  ]
  [U^t_{ezi}leq{R^t_z}
  ]
  [U^t_{bzi}leq{R^t_z}-(1-Y^t_{bzi})
  ]
  [U^t_{ezi}leq{R^t_z}-(1-Y^t_{ezi})
  ]
  [sum_{iin{I^t_{bzi}}}U^t_{bzi}=R^t_z
  ]
  [sum_{iin{I^t_{ezi}}}U^t_{ezi}=R^t_z
  ]

• 此时约束条件(6)、(7)变为：

• 那么(a=n^t_zsum_{iin{I^t_{bz}}}U^t_{bzi}r^t_{bzi})，(b=n^t_zsum_{iin{I^t_{ez}}}U^t_{ezi}r^t_{ezi})。约束(V^t_{bzi}leq{a}Y^t_{bzi})和(V^t_{ezi}leq{b}Y^t_{ezi})分别变为：

  [V^t_{bzi}leq{(n^t_zsum_{iin{I^t_{bz}}}U^t_{bzi}r^t_{bzi}})Y^t_{bzi}=n^t_zU^t_{bzi}sum_{iin{I^t_{bz}}}r^t_{bzi}Y^t_{bzi}
  ]
  [V^t_{ezi}leq{(n^t_zsum_{iin{I^t_{ez}}}U^t_{ezi}r^t_{ezi})}Y^t_{ezi}=n^t_zU^t_{ezi}sum_{iin{I^t_{ez}}}r^t_{ezi}Y^t_{ezi}
  ]

  • 已知(V^t_{bzi}geq{0})，当(Y^t_{bzi}=0)时，上面的第一条约束条件变为(V^t_{bzi}leq{0})，此时(V^t_{bzi})应为0；当(Y^t_{ezi}=1)时，上面的约束条件变为(V^t_{bzi}leq{n^t_zU^t_{bzi}r^t_{bzi}})，此时(V^t_{bzi})的取值应当为(0leq{V^t_{bzi}}leq{n^t_zU^t_{bzi}r^t_{bzi}})。

    综上和同理，在约束(V^t_{bzi},V^t_{ezi}geq{0})下，式(A.19) 和式(A.20) 被推导出：

  [V^t_{bzi}leq{a}Y^t_{bzi}quad{}→quad{}V^t_{bzi}leq{n^t_zU^t_{bzi}r^t_{bzi}}
  ]
  [V^t_{ezi}leq{b}Y^t_{ezi}quad{}→quad{}V^t_{bzi}leq{n^t_zU^t_{bzi}r^t_{bzi}}
  ]

  • 对于约束条件(V^t_{bzi}geq[{sum_{win{Z}}(S^t_{bwz}+S^t_{ewz})}]-a(1-Y^t_{bzi}))和(V^t_{ezi}geq[{sum_{win{Z}}(O^t_{bwz}+O^t_{ewz})}]-b(1-Y^t_{ezi}))，它们分别变为：

    [V^t_{bzi}geq[{sum_{win{Z}}(S^t_{bwz}+S^t_{ewz})}]-(n^t_zsum_{iin{I^t_{bz}}}U^t_{bzi}r^t_{bzi})(1-Y^t_{bzi})
    ]
    [V^t_{ezi}geq[{sum_{win{Z}}(O^t_{bwz}+O^t_{ewz})}]-(n^t_zsum_{iin{I^t_{ez}}}U^t_{ezi}r^t_{ezi})(1-Y^t_{ezi})
    ]

    当(Y^t_{bzi}=0)时，上面第一条约束条件变为(sum_{win{Z}}(S^t_{bwz}+S^t_{ewz})leq{n^t_zsum_{iin{I^t_{bz}}}U^t_{bzi}r^t_{bzi}})这与文中式（6）相同；当(Y^t_{bzi}=1)时，它则变为(V^t_{bzi}=sum_{win{Z}}(S^t_{bwz}+S^t_{ewz}))，而这又被约束条件(sum_{iin{I^t_{bzi}}}V^t_{bzi}={sum_{win{Z}}(S^t_{bwz}+S^t_{ewz})})包含。

    综上及同理，约束条件(V^t_{bzi}geq[{sum_{win{Z}}(S^t_{bwz}+S^t_{ewz})}]-a(1-Y^t_{bzi}))和(V^t_{ezi}geq[{sum_{win{Z}}(O^t_{bwz}+O^t_{ewz})}]-b(1-Y^t_{ezi}))均属于重复约束，可被消除。

由此，所有公式已全部被推出，但还多了两条约束：

• 对于约束条件(U^t_{bzi}leq{R^t_z}-(1-Y^t_{bzi}))有：

  • (Y^t_{bzi}=0)时，(R^t_zgeq{0})，该约束已存在；(Y^t_z=1)时，(U^t_{bzi}=R^t_{z})，该约束已被(sum_{iin{I^t_{bzi}}}U^t_{bzi}=R^t_z)所包含。

  • 综上及同理，约束条件(U^t_{bzi}leq{R^t_z}-(1-Y^t_{bzi}))和(U^t_{ezi}leq{R^t_z}-(1-Y^t_{ezi}))属于重复约束，均可被删除。

以上就是这篇论文公式全部的推导，上面是所使用的非线性化线性的方法简例如下。

三、简例

(1) 带有0-1变量的非线性规划问题

其中决策变量(x_1in{{0,1}}),(0leq{x_2}leq{a})

那么我们可以用下面的方法化为线性规划：

• 首先设一个新的决策变量(y=x_1x_2)，并将问题转化为：

  [yleq{ax_1}
  ]
  [yleq{x_2}
  ]
  [ygeq{x_2-a(1-x_1)}
  ]
  [ygeq{0}
  ]

• 由此，问题变为了线性问题

(2) 带分母变量的非线性规划问题

(s.t.)

• 令(z=frac{1}{4x+5y})，此时目标函数变为：((x+2y)z+3z)，但仍含有非线性项，此时我们又令：(xz=u,yz=v)，那么可以得到：

  [minquad{u+2v+3z}
  ]

  (s.t.)

  [6u+7vleq{8z}
  ]
  [9u+10vgeq{0}
  ]
  [u,v,zgeq{0}
  ]

• 解上面的线性规划问题，可得到(u,v,z)的精确解，之后可代入式子解方程，得到(x,y)的精确解。

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.fwqtg.net