本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
失真函数
假如某一信源 $mathbf{X}$ , 输出样值 $x_{i}$, $x_{i} in{a_{1}, a_{2}, ldots a_{n}}$ , 经试验信道传输后变成 $y_{j}$, $y_{j} in{b_{1}, b_{2}, ldots b_{m}}$ ,如果:
- $ x_{i}=y_{j}$ 没有失真
- $x_{i} neq y_{j}$ 产生失真
失真的大小, 用一个量来表示,即失真函数 $d(x_{i}, y_{j})$ , 以衡量用 $y_{j}$ 代替 $x_{i}$ 所引起的失真程度。
失真函数定义为:
$$
dleft(x_{i}, y_{j}right)=left{begin{array}{ll}
0 & x_{i}=y_{j} \
alpha & (alpha>0) x_{i} neq y_{j}
end{array}right.
$$
失真矩阵
将所有的 $d(x_{i}, y_{j})$ 排列起来, 用矩阵表示为:
$$
mathrm{d}=left[begin{array}{ccc}
dleft(a_{1}, b_{1}right) & cdots & dleft(a_{1}, b_{m}right) \
vdots & & vdots \
dleft(a_{n}, b_{1}right) & cdots & dleft(a_{n}, b_{m}right)
end{array}right] boldsymbol{n} times boldsymbol{m}
$$
例 : 设信源符号序列为 $mathbf{X}={mathbf{0}, mathbf{1}}$ , 接收端收到符号序列为 $mathrm{Y}={mathbf{0 , 1 , 2}}$ , 规定失真函数为
$$
begin{array}{c}
mathbf{d}(mathbf{0}, mathbf{0})=mathbf{d}(mathbf{1}, mathbf{1})=mathbf{0} ; mathbf{d}(mathbf{0}, mathbf{1})=mathbf{d}(mathbf{1}, mathbf{0})=mathbf{1} ; mathbf{d}(mathbf{0 , 2})=mathbf{d}(mathbf{1 , 2})=mathbf{0 . 5} \
d=left[begin{array}{lll}
0 & 1 & 0.5 \
1 & 0 & 0.5
end{array}right]
end{array}
$$
失真函数形式可以根据需要任意选取, 最常用的有:
- 均方失真: $d(x_{i}, y_{j})=(x_{i}-y_{j})^{2}$ 适用于连续信源
- 绝对失真: $d(x_{i}, y_{j})=|x_{i}-y_{j}|$
- 相对失真: $d(x_{i}, y_{j})=|x_{i}-y_{j}| /|x_{i}|$
- 误码失真: $d(x_{i}, y_{j})=delta(x_{i}-y_{j})={begin{array}{cc}0, & x_{i}=y_{j} \ 1, & text { 其他 }end{array}. $ 也称汉明失真,适用于离散信源
汉明失真矩阵(误码失真也叫汉明失真)
$$
d=left[begin{array}{cccc}
0 & 1 & cdots & 1 \
1 & 0 & cdots & 1 \
vdots & & & vdots \
1 & 1 & cdots & 0
end{array}right]
$$
对于二元对称信道 $(mathrm{m}=mathrm{n}), mathrm{X}={0,1}, mathrm{Y}={0,1}$ , 汉明失真矩阵:
$$
d=left[begin{array}{ll}
0 & 1 \
1 & 0
end{array}right]
$$
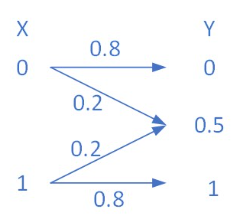
信道模型如下所示。采用汉明失真,请写出失真矩阵。
$$
d=left[begin{array}{lll}
0 & 1 & 1 \
1 & 1 & 0
end{array}right]
$$
平均失真
$x_{i}$ 和 $y_{j}$ 都是随机变量,所以失真函数 $d(x_{i}, y_{j})$ 也是随机变量,因此失真值只能用数学期望表示。
将失真函数的数学期望称为平均失真:
$$
bar{D}=sum_{i} sum_{j} pleft(a_{i}right) pleft(b_{j} mid a_{i}right) dleft(a_{i}, b_{j}right)
$$
- 失真函数 $d(x_{i}, y_{j})$ : 描述了某个信源符号通过传输后失真的大小
- 平均失真 $bar{D}$ : 描述某个信源在某一试验信道传输下的失真大小, 它对信源和信道进行了统计平均, 是从总体上描述整个系统的失真。
信道矩阵如下图所示,已知信源符号等概,采用汉明失真,求平均失真。
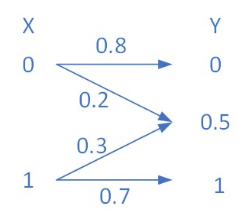
$$
begin{array}{c}
boldsymbol{p}(mathbf{0})=boldsymbol{p}(mathbf{1})=mathbf{0} . mathbf{5} \
boldsymbol{d}=left[begin{array}{lll}
mathbf{0} & mathbf{1} & mathbf{1} \
mathbf{1} & mathbf{1} & mathbf{0}
end{array}right] \
bar{D}=sum_{i} sum_{j} pleft(a_{i}right) pleft(b_{j} mid a_{i}right) dleft(a_{i}, b_{j}right) \
=mathbf{0 . 5} sum_{j} pleft(b_{j} mid mathbf{0}right) boldsymbol{d}left(mathbf{0}, b_{j}right) \
+mathbf{0 . 5} sum_{boldsymbol{j}} pleft(b_{j} mid mathbf{1}right) boldsymbol{d}left(mathbf{1}, b_{j}right) \
= 0.5(0.8*0 + 0.2*1 + 0*1)
+0.5(0*1+0.3*1+0.7* 0)= 0.25
end{array}
$$
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net