动动发财的小手,点个赞吧!

除了在网上找到的一些过度清理的数据集之外,缺失值无处不在。事实上,数据集越复杂、越大,出现缺失值的可能性就越大。缺失值是统计研究的一个令人着迷的领域,但在实践中它们往往很麻烦。
如果您处理一个预测问题,想要从 p 维协变量 X=(X_1,…,X_p) 预测变量 Y,并且面临 X 中的缺失值,那么基于树的方法有一个有趣的解决方案。这种方法实际上相当古老,但在各种数据集中似乎都表现得非常好。我说的是“缺失的属性标准”(MIA;[1])。虽然有很多关于缺失值的好文章(例如这篇文章),但这种强大的方法似乎有些未得到充分利用。特别是,不需要以任何方式插补、删除或预测缺失值,而是可以像完全观察到的数据一样运行预测。
我将快速解释该方法本身是如何工作的,然后提供一个示例以及此处解释的分布式随机森林 (DRF)。我选择 DRF 是因为它是随机森林的一个非常通用的版本(特别是,它也可以用来预测随机向量 Y),而且因为我在这里有些偏见。 MIA实际上是针对广义随机森林(GRF)实现的,它涵盖了广泛的森林实现。特别地,由于DRF在CRAN上的实现是基于GRF的,因此稍作修改后,也可以使用MIA方法。
当然,请注意,这是一个快速修复(据我所知)没有理论上的保证。根据缺失机制,分析可能会严重偏差。另一方面,处理缺失值的最常用方法没有任何理论保证,或者众所周知会使分析产生偏差,并且至少从经验上来看,MIA 似乎运作良好,并且
工作原理
回想一下,在 RF 中,分割的构建形式为 X_j
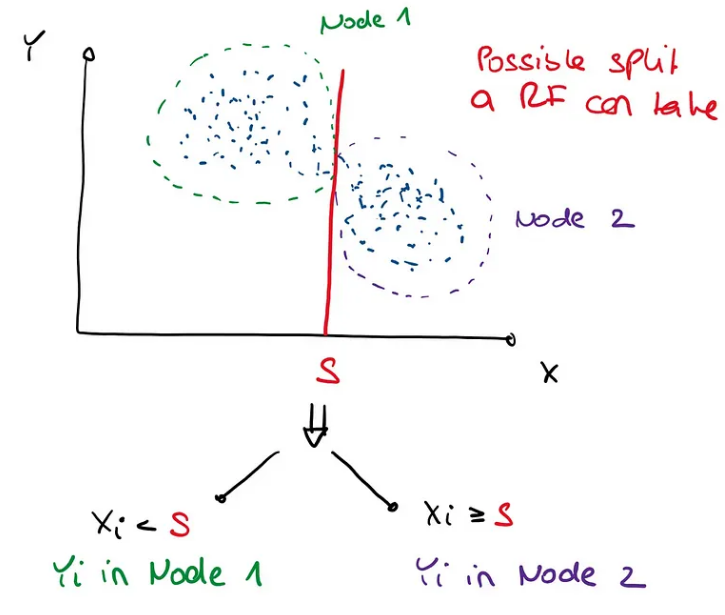
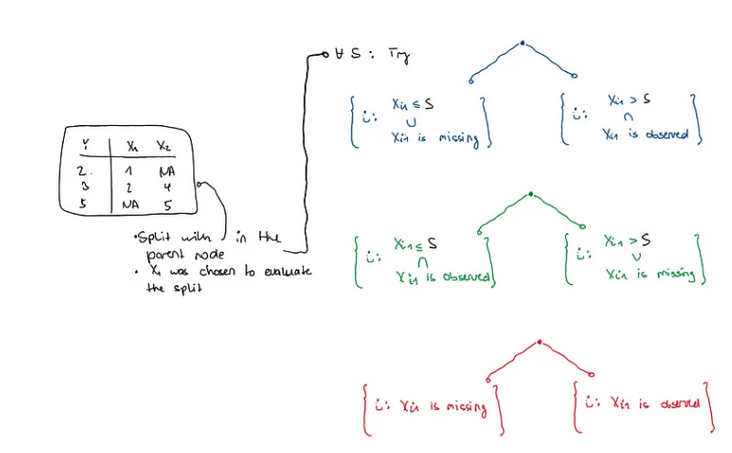
原论文的解释有点令人困惑,但据我了解,MIA 的工作原理如下:让我们考虑一个样本 (Y_1, X_1),…, (Y_n, X_n),
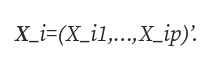
不缺失值的分割就是像上面那样寻找值S,然后将节点1中所有X_ij
- 对所有观测值 i 使用通常的规则,使得 X_ij 被观测到,如果 X_ij 丢失,则将 i 发送到节点 1。
- 对所有观测值 i 使用通常的规则,以便观测到 X_ij,如果缺少 X_ij,则将 i 发送到节点 2。
- 忽略通常的规则,如果 X_ij 缺失,则将 i 发送到节点 1;如果观察到 X_ij,则将 i 发送到节点 2。
遵循这些规则中的哪一个再次根据我们使用的 Y_i 的标准来决定。
例子
需要指出的是,CRAN 上的 drf 包尚未使用最新的方法进行更新。将来有一天,所有这些都将在 CRAN 上的一个包中实现。但是,目前有两个版本:
如果您想使用缺失值(无置信区间)的快速 drf 实现,您可以使用本文末尾附带的“drfown”函数。此代码改编自
lorismichel/drf: Distributional Random Forests (Cevid et al., 2020) (github.com)
另一方面,如果您想要参数的置信区间,请使用此(较慢的)代码
drfinference/drf-foo.R at main · JeffNaef/drfinference (github.com)
特别是,drf-foo.R 包含后一种情况所需的所有内容。
我们将重点关注具有置信区间的较慢代码,如本文所述,并考虑与所述文章中相同的示例:
set.seed(2)
n请注意,这是一个异方差线性模型,p=2,误差项的方差取决于 X_1 值。现在我们还以随机缺失 (MAR) 方式向 X_1 添加缺失值:
prob_na 这意味着每当 X_2 的值小于 -0.2 时,X_1 缺失的概率为 0.3。因此X_1丢失的概率取决于X_2,这就是所谓的“随机丢失”。这已经是一个复杂的情况,通过查看缺失值的模式可以获得信息。也就是说,缺失不是“随机完全缺失(MCAR)”,因为X_1的缺失取决于X_2的值。这反过来意味着我们得出的 X_2 的分布是不同的,取决于 X_1 是否缺失。这尤其意味着删除具有缺失值的行可能会严重影响分析。
我们现在修复 x 并估计给定 X=x 的条件期望和方差,与上一篇文章中完全相同。
# Choose an x that is not too far out
x然后我们还拟合 DRF 并预测测试点 x 的权重(对应于预测 Y|X=x 的条件分布):
## Fit the new DRF framework
drf_fit 条件期望
我们首先估计 Y|X=x 的条件期望。
# Estimate the conditional expectation at x:
condexpest值得注意的是,使用 NA 获得的值与上一篇文章中未使用 NA 的第一次分析得到的值非常接近!这确实令我震惊,因为这个缺失的机制并不容易处理。有趣的是,估计器的估计方差也翻倍,从没有缺失值的大约 0.025 到有缺失值的大约 0.06。
真相如下:
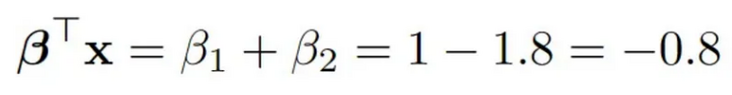
所以我们有一个轻微的错误,但置信区间包含事实,正如它们应该的那样。
对于更复杂的目标,结果看起来相似,例如条件方差:
# Estimate the conditional expectation at x:
condvarest这里估计值的差异有点大。由于真相被给出为
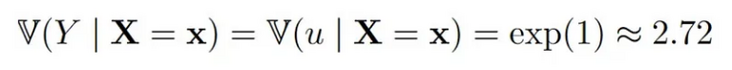
NA 的估计甚至稍微更准确(当然这可能只是随机性)。同样,(方差)估计量的方差估计随着缺失值的增加而增加,从 0.15(无缺失值)增加到 0.23。
结论
在本文中,我们讨论了 MIA,它是随机森林中分裂方法的一种改进,用于处理缺失值。由于它是在 GRF 和 DRF 中实现的,因此它可以被广泛使用,我们看到的小例子表明它工作得非常好。
然而,我想再次指出,即使对于大量数据点,也没有一致性或置信区间有意义的理论保证。缺失值的原因有很多,必须非常小心,不要因粗心处理这一问题而使分析产生偏差。 MIA 方法对于这个问题来说决不是一个很好理解的解决方案。然而,目前这似乎是一个合理的快速解决方案,它似乎能够利用数据缺失的模式。如果有人进行了更广泛的模拟分析,我会对结果感到好奇。
Code
require(drf)
drfown 本文由mdnice多平台发布
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
本书介绍 在处理机器学习问题时,通常有两种类型的数据(和机器学习模型) 监督数据:总是有一个或多个目标与之相关联。 无监督数据:没有任何目标变量。 有监督的问题比无监督的问题更容易解决。要求预测一个值的问题被称为监督问题。例如,…

