局部异常因子(Local Outlier Factor, LOF)通过计算样本点的局部相对密度来衡量这个样本点的异常情况,可以算是一类无监督学习算法。下面首先对算法的进行介绍,然后进行实验。
LOF算法
下面介绍LOF算法的每个概念,以样本点集合中的样本点$P$为例。下面的概念名称中都加了一个k-,实际上部分名称原文没有加,但是感觉这样更严谨一些。
k-邻近距离(k-distance):样本点$P$与其最近的第$k$个样本点之间的距离,表示为$d_k(P)$。其中距离可以用各种方式度量,通常使用欧氏距离。
k-距离邻域:以$P$为圆心,$d_k(P)$为半径的邻域,表示为$N_k(P)$。
k-可达距离:$P$到某个样本点$O$的k-可达距离,取$d_k(O)$或$P$与$O$之间距离的较大值,表示为
$reach_dist_k(P,O)=max{d_k(O),d(P,O)}$
也就是说,如果$P$在$N_k(O)$内部,$reach_dist_k(P,O)$取$O$的k-邻近距离$d_k(O)$,在$N_k(O)$外部则取$P$与$O$之间距离$d(P,O)$。需要注意k-可达距离不是对称的。
k-局部可达密度(local reachability density, lrd):$P$的k-局部可达密度表示为
$displaystyle lrd_k(P)=left(frac{sumlimits_{Oin N_k(P)}reach_dist_k(P,O)}{|N_k(P)|}right)^{-1}$
括号内,分子计算了$P$到其k-距离邻域内所有样本点$O$的k-可达距离之和,然后除以$P$的k-距离邻域内部的样本点个数进行平均。再加一个倒数,表示为密度,即$P$到每个点的平均距离越小,密度越大。可以推理出,如果$P$在所有$O$的k-邻域内部,其局部可达密度即为
$displaystyle lrd_k(P)=left(frac{sumlimits_{Oin N_k(P)}d_k(O)}{|N_k(P)|}right)^{-1}$
可以看出,如果$P$是一个离群点,那么它不太可能存在于$N_k(P)$中各点的k-距离邻域内,从而导致其局部可达密度偏小;如果$P$不是离群点,其局部可达密度最大取为上式。
实际上我有点奇怪为什么要用一个最大值来将距离作一个限制,也就是使用k-可达距离,而不是直接使用距离,即定义局部密度为下式
$displaystyle ld_k(P)=left(frac{sumlimits_{Oin N_k(P)}d(O,P)}{|N_k(P)|}right)^{-1}$
k-局部异常因子(Local Outlier Factor, LOF):$P$的k-局部异常因子表示为
$displaystyle LOF_k(P)=frac{frac{1}{|N_k(P)|}sumlimits_{Oin N_k(P)}lrd_k(O)}{lrd_k(P)}$
从直觉上理解:当$LOF_k(P)le1$时,表明$P$处密度比其周围点的平均密度大或相当,则$P$是内点;当$LOF_k(P)>1$时,表明$P$处密度比其周围点小,可以判别为离群(异常)点。
实验
LOF算法实现
实验设置样本维度为2以便可视化。由于样本点只包含连续值,实验默认设置$|N_k(P)|=k$。设置$k=5$,并将阈值设为2,即将LOF大于2的样本点视作异常。函数定义、抽样、计算以及可视化代码如下。
实验可视化结果如下图所示,其中红色点表示被标为异常的点,三角点表示实验设置的真实异常点。
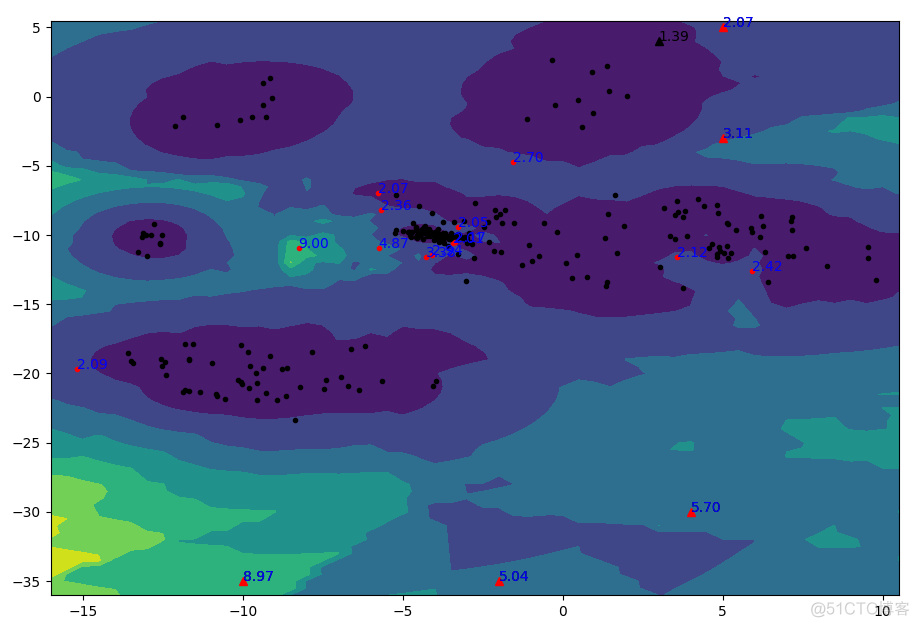
距离代替局部可达距离
根据前面的疑问,用距离代替局部可达距离进行相应实验。仅在get_LOFs函数处做了相关改动,并将阈值threshold改为2.5。get_LOFs函数修改如下。
可视化结果如下图所示
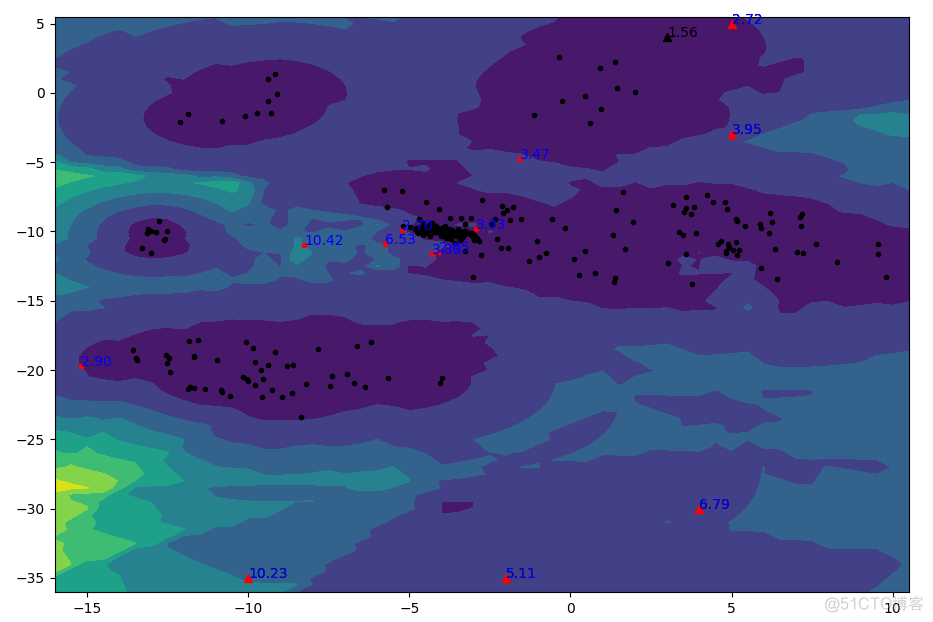
效果看起来和原始LOF差不多。至于用局部可达距离的理论解释,本文不再作深究,欢迎前来讨论。
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.e1idc.net

