折半查找算法(Binary Search Algorithm)是一种高效的搜索算法,常用于已排序的数组或列表中进行查找操作。它的核心思想是通过比较中间元素与目标值的大小关系来确定目标值在数组的哪一部分,从而缩小搜索范围。本文将详细介绍折半查找算法的原理、实现以及应用场景。
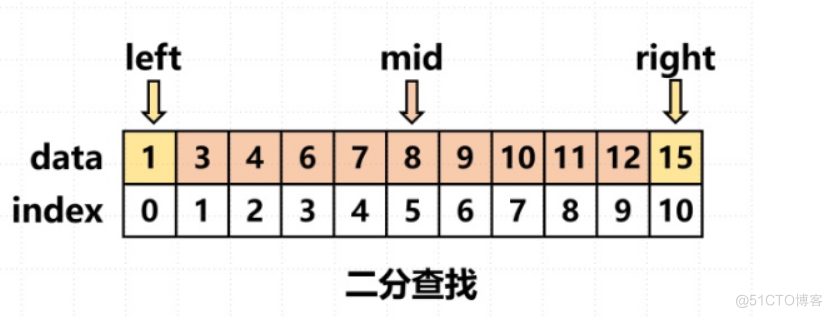
一、原理
折半查找算法利用了已排序数组的特性,采用分治策略,将问题分解为规模更小的子问题。它的基本思路如下:
- 将数组的左右边界定义为low和high,初始时low为0,high为数组的长度减1。
- 计算中间元素的下标mid,即mid = (low + high) / 2。
- 比较中间元素与目标值的大小关系: a. 如果中间元素等于目标值,则返回找到的位置。 b. 如果中间元素大于目标值,则新的右边界变为mid-1。 c. 如果中间元素小于目标值,则新的左边界变为mid+1。
- 重复以上步骤,直到找到目标值或者左边界大于右边界。
二、实现思路
例如,在升序的查找表 {10, 14, 19, 26, 27, 31, 33, 35, 42, 44} 中查找元素 33。初始状态下,搜索区域为整个查找表,用 low 记录搜索区域内第一个元素的位置,用 high 记录搜索区域内最后一个元素的位置。

图1 搜索区域是整个查找表
二分查找算法的查找过程是:
借助 ⌊(low+high)/2⌋ 公式,找到搜索区域内的中间元素。图 1 中,搜索区域内中间元素的位置是⌊(1+10)/2⌋=5,因此中间元素是 27,此元素显然不是要找的目标元素。
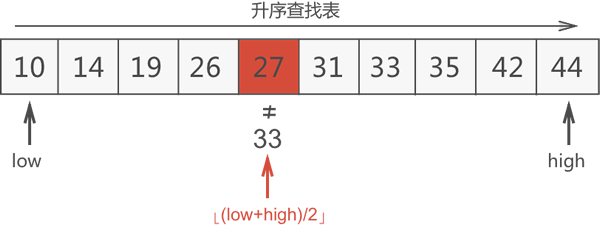
图2 中间元素 27 不是目标元素
整个查找表为升序序列,根据 27
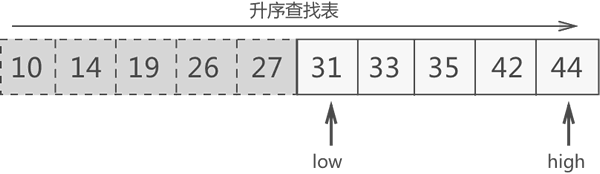
图3 更新搜索区域为 {31, 33, 35, 42, 44}
图 服务器托管网3 中,搜索区域内中间元素的位置是 ⌊(6+10)/2⌋=8,因此中间元素是 35,此元素不是要找的目标元素。
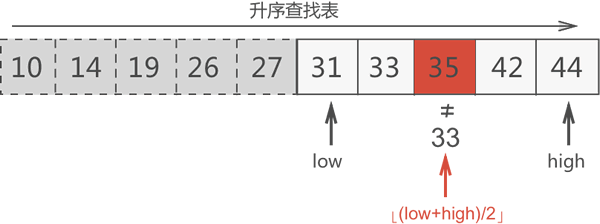
图4 中间元素 35 不是目标元素
根据 35>33,可以判定 33 位于 35 左侧的区域,更新搜索区域。
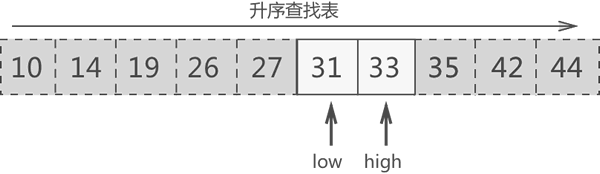
图5 更新搜索区域 {31, 33}
图 5 中,搜索区域内中间元素的位置是 ⌊(6+7)/2⌋=6,因此中间元素是 31,此元素不是要找的目标元素。
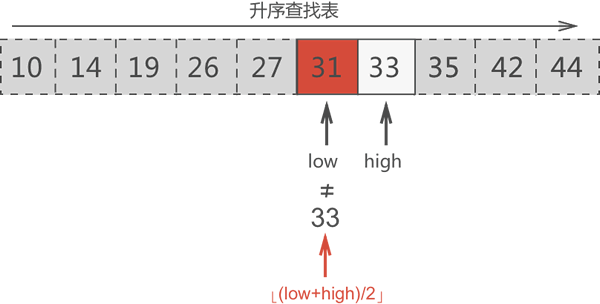
图6中间元素 31 不是目标元素
根据 31
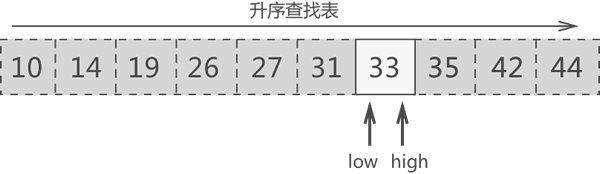
图7 更新搜索区域 {33}
图 7 中,搜索区域内中间元素的位置是 ⌊(7+7)/2⌋=7,因此中间元素是 33,此元素就是要找的目标元素。
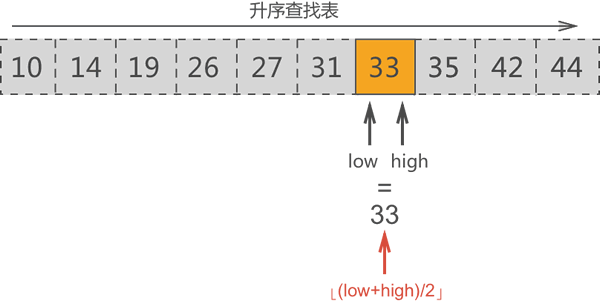
图8 成功找到目标元素
找到了目标元素 33,二分查找算法执行结束。下面的动画演示了整个二分查找算法的执行过程:

图9 二分查找算法
所谓二分查找算法,其实就是不断地将有序查找表“一分为二”,逐渐缩小搜索区域,进而找到目标元素。当查找表中没有目标元素时(比如图 8 中的元素 33 为 32),最终会出现 low>hig服务器托管网h 的情况,此时就表明查找表中没有目标元素,查找失败。
三、实现
如何利用折半查找算法在已排序数组中查找特定元素的位置:
#include
#include
#define keyType int
typedef struct {
keyType key; //查找表中每个数据元素的值
//如果需要,还可以添加其他属性
}ElemType;
typedef struct {
ElemType* elem; //存放查找表中数据元素的数组
int length; //记录查找表中数据的总数量
}SSTable;
//创建查找表
void Create(SSTable* st, int length) {
int i;
st->length = length;
st->elem = (ElemType*)malloc((length) * sizeof(ElemType));
printf("输入表中的元素:n");
//根据查找表中数据元素的总长度,在存储时,从数组下标为 1 的空间开始存储数据
for (i = 0; i elem[i].key));
}
}
//折半查找算法
int Search_Bin(SSTable ST, keyType key) {
int low = 0; // 初始状态 low 指针指向第一个关键字
int high = ST.length - 1; // high 指向最后一个关键字
int mid;
while (low key) // 如果mid指向的关键字较大,则更新 high 指针的位置
{
high = mid - 1;
}
// 反之,则更新 low 指针的位置
else {
low = mid + 1;
}
}
//未在查找表中找到目标元素,查找失败
return -1;
}
int main() {
int len, key;
int location;
SSTable st = { 0 };
printf("请输入查找表的长度:");
scanf("%d", &len);
Create(&st, len);
printf("请输入查找数据的关键字:");
scanf("%d", &key);
location = Search_Bin(st, key);
//如果返回值为 -1,证明查找表中未查到 key 值,
if (location == -1) {
printf("查找表中无目标元素");
}
else {
printf("目标元素在查找表中的位置为:%d", location + 1);
}
free(st.elem);
return 0;
}四、应用场景
折半查找算法的时间复杂度为O(logN),其中N是数组的长度。相比于线性搜索算法的时间复杂度O(N),折半查找算法在大规模数据集上具备明显的优势。因此,它广泛应用于以下场景:
- 数组或列表的查找:当我们需要在一个已排序的数组或列表中查找某个特定元素时,可以使用折半查找算法进行高效的搜索。
- 数据库索引:数据库系统通常会采用B树(或B+树)作为索引结构,而B树的查找操作就是基于折半查找算法实现的。通过利用折半查找的特性,可以快速定位到数据库中的记录。
- 排序算法优化:一些排序算法,如快速排序(Quick Sort)和归并排序(Merge Sort),在内部实现中使用了折半查找算法。通过将数组划分为更小的子数组并采用折半查找的方式进行排序,可以提高算法的性能。
五、总结
二分查找算法的时间复杂度为O(logn),平均查找长度 ASL=log2(n+1)-1。和顺序查找算法相比,二分查找算法的执行效率更高。二分查找算法只适用于有序的静态查找表,且通常选择用顺序表表示查找表结构。
综上所述,折半查找算法是一种高效的搜索算法,适用于已排序的数组或列表。它通过比较中间元素与目标值的大小关系来确定目标值所在的范围,从而缩小搜索的范围,减少了搜索的时间复杂度。无论是在数据结构、数据库索引还是游戏开发等领域,折半查找算法都发挥着重要的作用。
部分内容引用:https://data.biancheng.net/
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: 深入探索 Django Rest Framework
这篇文章会详细介绍Django REST Framework的核心组成部分,包括Serializers、ViewSets、Routers、权限和认证系统以及测试和调试工具。文章从基础开始,逐步深入,旨在帮助读者掌握使用Django REST Framework…

