MATLAB中向量和矩阵的基本运算

设A,B两个矩阵

1.A+B，A-B
2.k*A
3.A*B
4.AB 左除 A-1B，A必须为方阵
5.A/B 右除 AB-1，B必须为方阵
6.det(A) 求|A|，A必须为方阵
7.inv(A)或A-1
8.A^n
9.A’或transpose(A)
10.rank(A)
rref(A) 矩阵行变化化简，求矩阵A阶梯形的行最简形式
例题:

矩阵的变换与分解及其在MATLAB中的实现

矩阵的对角元素

函数diag将一个矩阵的对角元素提取出来

diag(A) 由矩阵A的对角线元素得到一个列向量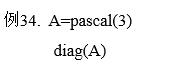

用该函数来产生第k阶对角线上的元素

diag(A,k)
其中,k=0表示主对角线;
k>0表示在主对角线以上;
k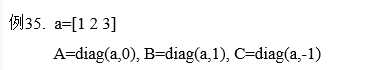

函数blkdiag可以根据输入创建一个分块对角矩阵

S=blkdiag(a,b,c,…)
功能：根据输入的a,b,c等参数构造一个分块对角矩阵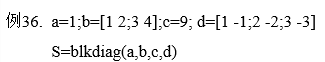

矩阵的分解

(1) 矩阵的奇异值分解 s=svd(A)
[U,S,V]=svd(A)
[U,S,V]=svd(A,0)
(2) 矩阵的LU分解 [L,U]=lu(A)
(2) 矩阵的QR分解 [Q,R]=qr(A)
(2) 矩阵的Cholesky分解 C=chol(A)

MATLAB中矩阵特征值和特征向量的求解方法

矩阵的特征值和特征向量

d=eig(A) 返回方阵A的全部特征值组成的特征向量d
[V,D]=eig(A) 返回矩阵A的特征值D与特征向量矩阵V,满足AV=VD
poly(A) 求矩阵A的特征多项式

注：求矩阵A的特征根 D=roots(poly(A)) 。

矩阵的相似对角化

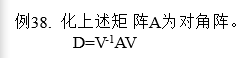
线性方程组的直接求解法在MATLAB中的实现

齐次线性方程组的直接求解法

A=[1 1 1 1 1;3 2 1 1 -3;0 1 2 2 6;5 4 3 3 -1]; B=null(A,‘r’);

syms k1 k2 k3; x=k1B(:,1)+k2B(:,2)+k3*B(:,3)

非齐次线性方程组的直接求解法

求逆法

对AX=B，若|A|不等于0，则解由inv(A)*B获得

左除法和右除法

A=[2 3 1 4;1 -2 4 -5;3 8 -2 13; 4 -1 9 -6];
rref(A) %转化为矩阵简最简阶梯式

符号方程组的求解方法

线性方程组AX=B的符号解

X=linesolve(A,B) %只给出特解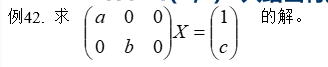

syms a b c;
A=[a 0 0;0 b 0]; B=[1;c]
X=linesolve(A,B)

非线性方程组的符号姐

[x1,x2,x3,…]=solve(e1,e2,e3,…)

e1=sym(‘a+b+x=y’);
e2=sym(‘2ax-by=-1’);
e3=sym(‘2(a+b)=x+y’);
e4=sym(‘ay+bx=4’);
[a,b,x,y]=solve(e1,e2,e3,e4)

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net