使用到的是scipy库
线性规划指的是目标模型均为线性,除此以外的都是非线性规划,使用scipy提供的方法对该类问题进行求解。
from scipy.optimize import minimize
import numpy as np
#定义目标函数
def fun(服务器托管网args):
a,b,c,d = args
v = lambda x: (a+x[0])/ (b+x[1]) - c*x[0] + d*x[2]
return v
#定义约束条件
def con(args):
# 约束条件 分为eq 和ineq
# eq表示 函数结果等于0 ; ineq 表示 表达式大于等于0
x1min,x1max,x2min,x2max,x3min,x3max = args
cons = ({'type':'ineq', 'fun': lambda x : x[0] - x1min},
{'type':'ineq', 'fun': lambda x : -x[0] + x1max},
{'type':'ineq', 'fun': lambda x : x[1] - x2min},
{'type':'ineq', 'fun': lambda x : -x[1] + x2min},
{'type':'ineq', 'fun': lambda x : x[2] - x3min},
{'type':'ineq', 'fun': lambda x : -x[2] + x3min},
)
return cons
#定义常量值
args = (2,1,3,4)
服务器托管网
#设置变量约束条件
args2 = (0.1,0.9,0.1,0.9,0.1,0.9)
cons = con(args2)
#设置初始随机值
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP', constraints=cons)
res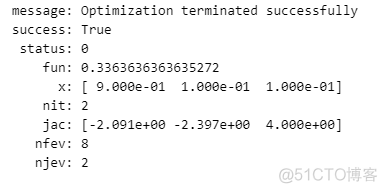
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: 展会回顾 | 2023元宇宙生态博览会圆满落幕,3DCAT荣获“元宇宙交互技术奖”
2023年5月10日-5月12日,一场涵盖了元宇宙终端头显、数字文娱、数字艺术、数字运动、数字多媒体展陈设计、数字展厅展馆、科技文旅、夜游演艺、沉浸式KTV/酒吧等多个领域的元宇宙商业盛会——2023第2届世界元宇宙生态博览会在广州广交会展馆A区3.2馆、4.…

