数据结构与算法（三）–栈 一、前言 二、栈（Stack） 三、栈的应用 四、栈的实现 五、栈的另一个应用–括号匹配（编译器）

Posted on by hackdl

一、前言

前两篇文章我们学习了第一个数据结构，数组，且从底层通过java实现了数组的构建和增删改查的操作功能，并且通过resize操作使我们的数组可以动态的扩容或者缩容。且我们知道数组最大的优点就是在索引有语义的情况下，查询和修改操作会非常的快，反之我们就得遍历寻找元素。我们还了解了时间复杂度，渐进复杂度，分摊复杂度和复杂度震荡等知识，分析动态数组相关操作的时间复杂度并且优化了resize操作。那么从这一章我们要学习另一种线性数据结构-栈。

二、栈（Stack）

  • 栈也是一种线性结构
  • 相比数组，栈对应的操作是数组的子集
  • 我们只能从一端添加元素，也只能从同一端取出元素
  • 这一端我们称为栈顶

当我们这样限定我们的数组形成了栈这样一个数据结构之后，它却可以在我们计算机组成逻辑有着非常非常重要的作用。

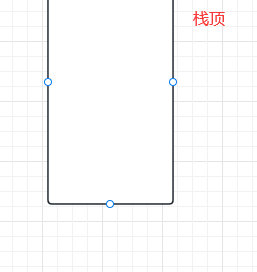
然后我们只能往栈顶这一端放入数据，这个放数据的过程通常我们称之为入栈：

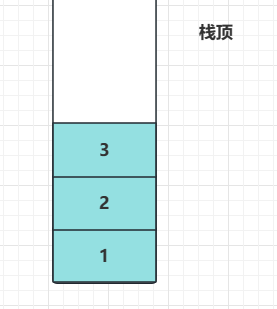
需要注意的是，3只能放在2的上面，不能放在1和2的中间或者1的下面，这就是我们只能往栈顶这一端放入数据这个的体现。
如果我们现在想从栈取出元素，我们只能取出先取出3这个元素，因为3目前在栈顶，我们拿不到2和1，甚至从用户角度根本看不到2和1这两个元素。用户只能看到栈顶的元素，我们将元素从栈顶取出的过程叫作出栈。且出栈也体现了只能从同一端（栈顶）取出元素。

  • 从放入和取出的过程我们可以看到，栈是一种后进先出的数据结构（LIFO-Last In First Out）。

我们从刚才的例子可以看到，3是我们最后放入栈的元素，但却是第一个从栈被取出的元素

三、栈的应用

  1. 无处不在的undo操作（撤销）

原理就是栈的应用。
例如我现在在文本里输入“沉迷”，对于这个动作，我们编辑器就会记录下来，这个记录动作其实就是把动作放进栈中，然后打入“学习”，接着本来打入“无法自拔”结果打成了“不法自拔”，由于打错也算一个动作这个时候就会把这些入栈过程体现为：

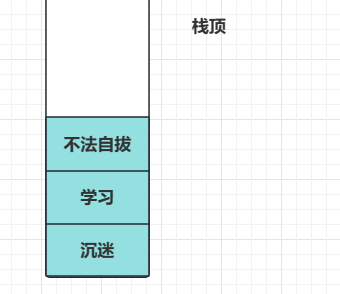
然后你意识到打错了，这个时候撤销，你执行撤销操作的过程就是从栈中拿出栈顶的元素，通过栈顶的元素来确认你最近的操作是什么，所以这次撤销操作就是把“不法自拔”从栈拿出然后删掉：

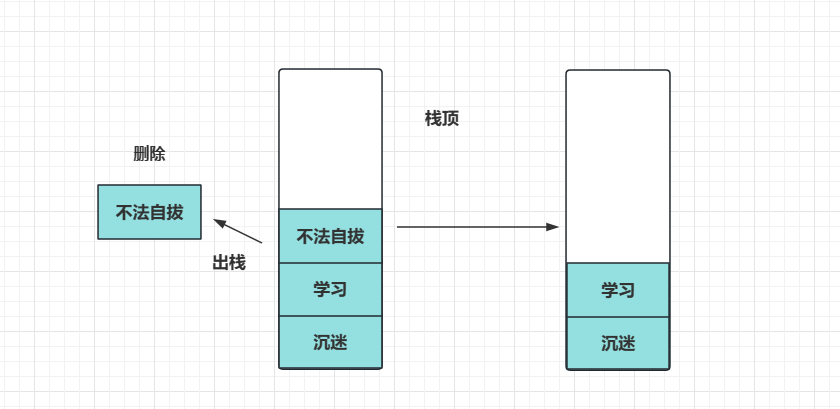
然后就可以继续重复之前的操作从而打入正确的文本。

  1. 程序调用的系统栈
    事实上，在我们程序调用的过程中经常会出现在一个逻辑的中间先终止，然后跳到另外的逻辑去执行，例如子函数的调用，这个过程中计算机就需要使用一个系统栈，其实就是栈的数据结构来记录我们程序的调用过程。
    例如，下面有三个函数，其中A在第二行代码执行B()，B()在第二行代码执行C()，C()直接执行完普通的三行代码，没有子函数调用。那么对于我们计算机来说当执行A第二行代码的时候，此时程序暂时中断，转而去执行B函数，此时我们的系统栈就会记录一个信息叫作A2，代表之前这个程序执行到A的第二行了，这里进行了中断去执行B函数了；同理执行B第二行代码的时候，转而去执行C函数暂时中断B函数，系统栈会记录一个信息叫B2

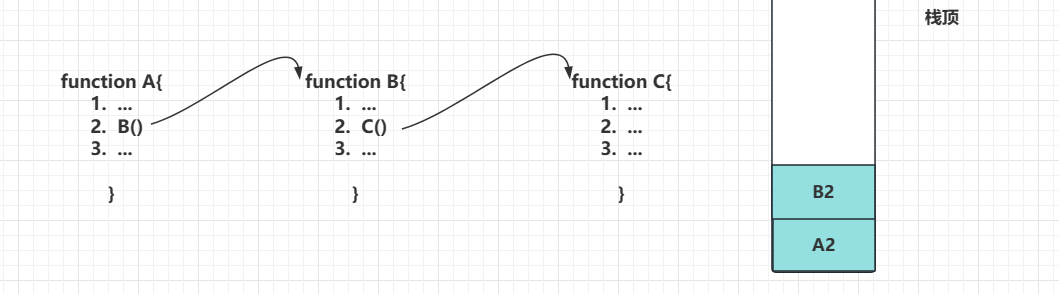
    当C函数执行完了后，计算机就会遇到个问题，下面需要去执行什么，答案就是查看系统栈，对于系统栈来说，栈顶是B2，它就知道执行到B函数第二行的时候中断了，我就可以跳回到B2这个位置继续执行了，此时B2出系统栈并且删除，同理执行完B后看到系统栈还有A2，跳回到A2这个位置继续执行完整个程序。此时系统栈是空的，整个过程才算执行完毕。

这就是我们编程的时候进行子过程调用的时候，当一个子过程完成后可以自动的回到上层函数调用中断的位置，继续执行下去的原因，因为背后有一个系统栈，它可以记录每一次调用过程中中断的那个点。
基于这个原理的算法例如递归就是类似这样实现的。

四、栈的实现

上一节说了栈的定义和应用，其实大家会发现栈的应用非常重要，但是它实现起来其实非常简单，我们只需要实现以下方法即可：
Stack

  • void push(E) 入栈
  • E pop() 从栈中拿出元素，出栈
  • E peek() 查看当前栈顶元素，也可以叫top()
  • int gitSize() 查看栈里一共有多少元素
  • boolean isEmpty() 查看栈是否为空

从用户的角度看，支持这些操作就好，和数组差不多，用户不想担心怎样resize的，他只需要知道数组是动态的，我可以通过数组添加删除元素是正常的就好了。对于栈亦是如此
对于具体底层实现，用户不关心，实际底层有多种实现方式，但是这里我们只采用基于动态数组的方式实现的栈。由于栈本身主要就是上面说的那5种操作，我们完全可以将Stack本身定义为一个接口，接口定义上面5个操作，然后写一个具体的实现类叫作ArrayStack通过数组的方式具体实现这5个操作。
ps:此次数组栈的实现方式需要前面文章动态数组的实现的基础，所以最好需要去查看动态数组的实现这篇博客，有了动态数组的实现基础，我们会发现数组栈的实现就非常简单：
1、首先我们需要编写Stack接口，定义5个基础操作，代码如下：

public interface StackT> {
	int getSize();
	boolean isEmpty();
	void push(T t);
	T pop();
	T peek();
}

2、编写ArrayStack类实现Stack接口，实现5个操作的方法，代码如下：

import com.mbw.array.DynamicArray;

public class ArrayStackT> implements StackT> {
	private DynamicArrayT> dynamicArray;

	public ArrayStack(int capacity){
		this.dynamicArray = new DynamicArray>(capacity);
	}

	public ArrayStack(){
		this.dynamicArray = new DynamicArray>();
	}

	@Override
	public int getSize() {
		return dynamicArray.gitSize();
	}

	@Override
	public boolean isEmpty() {
		return dynamicArray.isEmpty();
	}

	@Override
	public void push(T t) {
		dynamicArray.addLast(t);
	}

	@Override
	public T pop() {
		return dynamicArray.removeLast();
	}

	@Override
	public T peek() {
		return dynamicArray.getLast();
	}

	@Override
	public String toString() {
		return "ArrayStack{" +
				"top = " + peek() +
				'}';
	}
}

其实这里说一下我一开始实现的误解的点，我认为栈顶等于数组第一个位置，所以我认为push和pop对应的不应该是addLast和removeLast,而是addFirst和removeFirst.peek也是getFirst()。但是这样说明我们对栈的定义是有错误的，其实我们只需要保证放入元素和去除元素是同一端即可，此时这个”同一端”不管是从数组头还是数组尾，其实都是可以的。那么我们当然选择addLast和removeLast啊，addFirst和removeFirst时间复杂度铁打的O(n)，而addLast和removeLast从均摊复杂度角度分析其实是O(1),效率更高。
然后我们可以试一下我们编写的栈：

public static void main(String[] args) {
		ArrayStackString> stringArrayStack = new ArrayStack>();
		stringArrayStack.push服务器托管网("沉迷");
		stringArrayStack.push("学习");
		stringArrayStack.push("不法");
		String pop = stringArrayStack.pop();
		System.out.println(pop);
		stringArrayStack.push("无法自拔");
		System.out.println(stringArrayStack.peek());
		System.out.println(stringArrayStack.toString());
	}


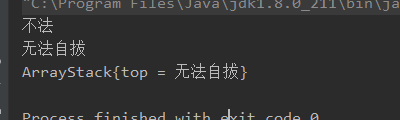
对于toString很多小伙伴可能会有疑惑为什么不把栈的所有元素打出来，其实从用户角度而言，栈这个数据结构用户只需关注栈顶的元素，我们从原则上也不应该把栈的中间元素给展示出来。不过自己学习的话可以将成员变量array的详情打印出来便于我们查看分析问题。这里就不做过多讲述。
而对于复杂度分析，除了之前说的push和pop从均摊复杂度角度分析都是O(1)，而peek()，getSize()，isEmpty()这几个操作很明显都是O(1)的，所以栈的性能是非常良好的。

五、栈的另一个应用–括号匹配（编译器）

想必很多干开发的朋友会很熟悉，例如我们编程的时候使用小括号，中括号的逻辑，或者我们写块逻辑，无论是for,if,while或者定义一个函数或者类都需要使用大括号，经常会有这种括号套括号的情况，在这种情况下，如果我们的括号匹配不成功的话，那我们的编译器就会报错，而这个原理就是应用栈。
本章我们会通过leetcode的一个题目通过编程的方式完成这个应用—20. 有效的括号
那么这题我们来看看如何通过栈来解决该问题：
首先假设字符串为([{}])
我们先从头开始，将字符串为左括号的入栈。如下图：


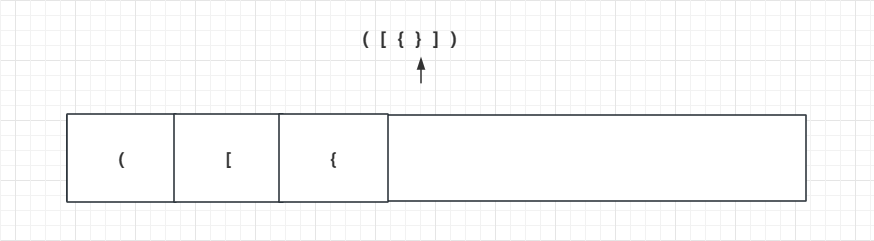
直到遍历字符串到第一个右括号的时候，这个时候出栈，将栈的第一个元素和当前字符做匹配，以此类推，如果最后都匹配上了，栈一定为空。如果栈不为空，说明有多的左括号。
而一旦没匹配上，则直接返回false。例如下图大括号和栈顶的中括号不匹配：

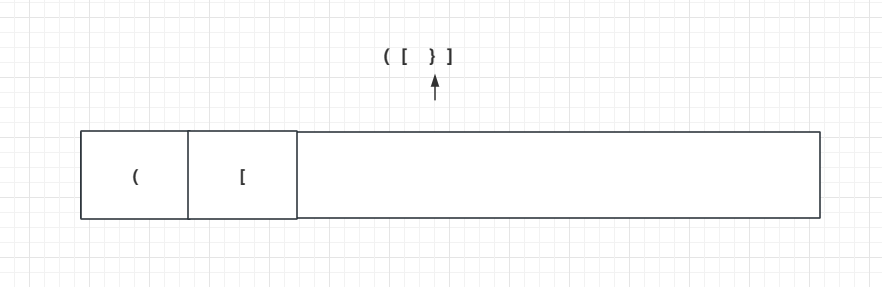
总结一句话就是：
栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素
接着我们掌握了原理，就可以编程解决了，这里我们不使用我们自定义的ArrayStack解决，而是通过java.util.Stack解决，其实熟悉的小伙伴会发现我们自己编写的ArrayStack和Stack的方法是一致的。
那么逻辑如下

class Solution {
	public boolean isValid(String s) {
	    //如果字符串长度不是偶数，那么肯定不匹配，返回false
		if (s.length() % 2 == 1){
			return false;
		}
		StackCharacter> stack = new Stack>();
		for (int i = 0; i  s.length(); i++) {
			char c = s.charAt(i);
			//如果是左括号则入栈
			if (c == '(' || c == '[' || c == '{') {
				stack.push(c);
			} else {
				//如果此时栈是空的，那么说明没有左括号只有右括号，那肯定是不匹配的，直接返回false
				if (stack.isEmpty()) {
					return false;
				}
				if (!validatePopAndChar(stack, c)) {
					return false;
				}
			}
		}
		//for循环结束后如果栈还有元素那么说明存在未匹配多余的左括号，返回false，否则返回true
		return stack.isEmpty();
	}

服务器托管网	private boolean validatePopAndChar(StackCharacter> stack, char c) {
	     //不是左括号，出栈和左括号匹配
		Character pop = stack.pop();
		if (c == ')' && pop != '(') {
			return false;
		}
		if (c == ']' && pop != '[') {
			return false;
		}
		return c != '}' || pop == '{';
	}
}

最后可以通过。

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net

相关推荐: [WPF]原生TabControl控件实现拖拽排序功能

在UI交互中，拖拽操作是一种非常简单友好的交互。尤其是在ListBox，TabControl，ListView这类列表控件中更为常见。通常要实现拖拽排序功能的做法是自定义控件。本文将分享一种在原生控件上设置附加属性的方式实现拖拽排序功能。 该方法的使用非常简单…

服务器托管，北京服务器托管，服务器租用，机房机柜带宽租用

服务器托管

咨询：董先生

电话13051898268 QQ/微信93663045！

上一篇:
下一篇: