树是一种非线性数据结构,是由n (n>=0)个有限节点组成的一个具有层次关系的集合。树的逻辑结构看起来像一棵倒挂的树,根朝上,叶子朝下。
树一般是递归定义的,每一棵树都可以认为是由根和其子树构成,且各个子树不相交。
树
树的相关概念
节点的度:一个节点含有的子树的个数称为该节点的度;
叶节点或终端节点:度为 0 的节点称为叶节点;
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的度:一棵树中,最大的节点的度称为树的度;
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次;
堂兄弟节点:双亲在同一层的节点互为堂兄弟
节点的祖先:从根到该节点所经分支上的所有节点
子孙:以某节点为根的子树中任一节点都称为该节点的子孙
森林:由 m(m>0)棵互不相交的树的集合称为森林
树的表示
树最常用“左孩子右兄弟表示法”表示。在每个结点中定义两个指针,其中一个指针指向该结点的第一个孩子结点,另一个指针指向该节点右侧的第一个兄弟结点。这种表示方法可以表示所有结点个数的树。

树的实际应用
树一般用来表示文件系统的目录结构。
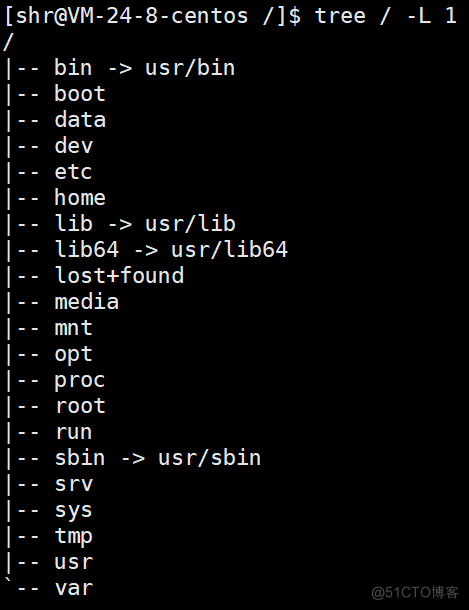
二叉树
二叉树是一棵树,其中每个节点都不能有多于两个的孩子节点,即二叉树节点的度在 [0, 2] 之间;二叉树是有序树,二叉树的左、右孩子次序不能颠倒。
二叉树具有以下性质:
- 一棵有 n 个结点的二叉树有 n – 1 条边;
- 度为 0 的结点数总比度为 2 的结点数多 1,即 n0 = n2 + 1;
- 若规定根结点的高度为 1,则一棵非空二叉树第 i 层的节点个数最多为2^(i – 1)
满二叉树和完全二叉树
一个二叉树,如果每一层的结点数都达到最大值,则这个二叉树就是满二叉树。若规定根节点的高度为 1,则一棵高度为 h 的满二叉树的结点个数为

完全二叉树是由满二叉树引出的,一棵深度为 h 的完全二叉树,其前 h – 1层都是满的,第 h 层的节点从左到右依次排列。一棵有 n 个结点的完全二叉树的高度为 logn 向上取整。
满二叉树是一种特殊的完全二叉树。
二叉树的顺序结构
普通的二叉树不适合用数组存储,因为会存在大量的空间浪费,而完全二叉树适合用数组存储,因为完全二叉树的非空节点是连续的。使用数组进行二叉树存储最常见的例子就是堆。

堆的概念和实现
堆是一种非传统的数据结构,它不止用来存储数据,而且使数据排列具有一定的性质和规律,使其便于在数据中找到最具优先权的一个。
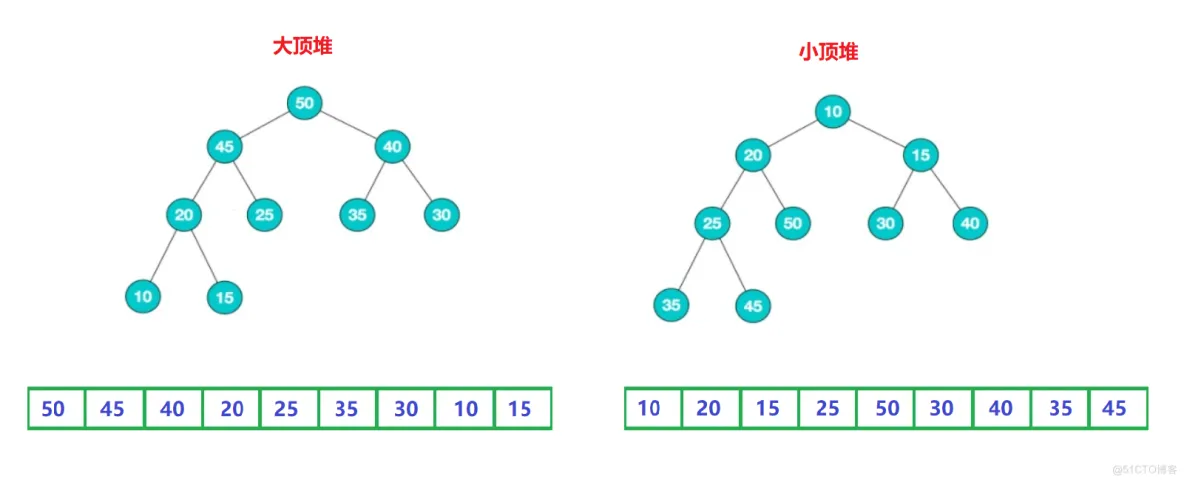
堆的逻辑结构是一棵完全二叉树,物理结构是一个数组,根据成立条件,堆主要分为两种类型:
- 大根堆,所有节点的值大于或等于其子节点的值
- 小根堆,所有节点的值小于或等于其子节点的值
关于堆的具体实现,以及堆的性质和应用,请参考数据结构之优先队列。
二叉树的链式结构
一般的二叉树更适合用链式结构实现,在树结点(TreeNode)中定义两个指针 leftChild 和 rightChild,分别指向该节点的左孩子和右孩子,对应节点进行链接即构成二叉树的链式结构。
二叉树的遍历
二叉树是递归定义的,对二叉树的大部分操作也是基于递归。
前、中、后序遍历
二叉树的前序遍历(PreOrder)是按照“根、左子树、右子树”顺序进行遍历堆的,二叉树的前序遍历属于深度优先搜索(DFS)。
void PreOrder(BTNode* root)
{
if(root == NULL) {
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOrder(root->leftChild);
PreOrder(root->rightChild);
}二叉树的中序遍历(InOrder)是按照 “左子树、根、右子树” 顺序进行遍历的;二叉树的后序遍历(PostOrder)是按照 “左子树、右子树、根” 顺序进行遍历的。
层序遍历
对二叉树进行层序遍历的基本思路是“出上一层,带下一层”,这就需要用到队列。具体操作为:当出队头结点时,将队头结点的左非空孩子结点和右非空孩子结点入队列,直至队列为空。
二叉树的层序遍历属于广度优先搜索(BFS)。
解决链式二叉树问题的基本思想
分治是解决二叉树问题的基本思想。当面对一个关于二叉树的问题时,要考虑将该问题拆解为规模较小的子问题,然后对二叉树进行递归操作。
关于二叉树的基本问题一般有:
- 求二叉树的深度
- 求二叉树的结点个数
- 求二叉树叶子结点的个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL) {
return 0;
}
if (root->leftChild == NULL &&
root->rightChild == NULL) {
return 1;
}
return BinaryTreeLeafSize(root->leftChild) +
BinaryTreeLeafSize(root->rightChild);
}- 求二叉树某层的结点个数
int TreeKLevel(BTNode* root, int k)
{
if (root == NULL) {
return 0;
}
if (k == 1) {
return 1;
}
return TreeKLevel(root->leftChild, k - 1) +
TreeKLevel(root->rightChild, k - 1);
}- 查找二叉树中值为 x 的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataTypt x)
{
if (root == NULL || root->data == x) {
return root;
}
//向左子树寻找
BTNode* tmp = BinaryTreeFind(root->leftChild, x);
if (tmp) {
return tmp;
}
//向右子树寻找
tmp = BinaryTreeFind(root->rightChild, x);
if (tmp) {
return tmp;
}
}- 判断单值二叉树
- 判断相等二叉树
- 判断对称二叉树
bool JudgeTree(struct TreeNode* lRoot, struct TreeNode* rRoot)
{
if(lRoot == NULL && rRoot == NULL) {
return true;
}
if(!lRoot || !rRoot) {
return false;
}
if(lRoot->val != rRoot->val) {
return false;
}
return JudgeTree(lRoot->left, rRoot->right) &&
JudgeTree(lRoot->right, rRoot->left);
}
bool isSymmetric(struct TreeNode* root)
{
if(root == NULL) {
return true;
}
return JudgeTree(root->left, root->right);
}- 判断完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL) {
QueuePush(&q, root);
}
BTNode* front = QueueFront(&q);
while (front != NULL)
{
QueuePop(&q);
QueuePush(&q, front->leftChild);
QueuePush(&q, front->rightChild);
front = QueueFront(&q);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL) {
return false;
}
}
return true;
}二叉树的创建和销毁
二叉树可以由其中序遍历结果和前序、后序遍历结果中的某一个结合,判断出其完整结构;或者根据前序带空遍历结果、中序遍历带空结果和后序带空遍历结果中的某一个判断出其完整结构。
从前序与中序遍历序列构造二叉树
class Solution
{
private:
unordered_map index;
private:
TreeNode* RecBuildTree(vector& preorder, vector& inorder,
int pre_left, int pre_right, int in_left, int in_right)
{
if(pre_left > pre_right){
//全部遍历完成,结束递进
return nullptr;
}
int pre_root = pre_left;//前序中的根(的索引)
int in_root = index[preorder[pre_root]];//获取中序中的根
int left_size = in_root - in_left;//计算左树大小
TreeNode* newRoot = new TreeNode(preorder[pre_root]);//构造根
//递归构造左树
newRoot->left = RecBuildTree(preorder, inorder,
pre_root + 1, pre_left + left_size, in_left, in_root - 1);
//递归构造右树
newRoot->right = RecBuildTree(preorder, inorder,
pre_left + left_size + 1, pre_right, in_root + 1, in_right);
return newRoot;
}
public:
TreeNode* buildTree(vector& preorder, vector& inorder)
{
int n = preorder.size();
for(int i = 0; i 从先序遍历序列构造二叉树
typedef struct TreeNode
{
char data;
struct TreeNode* leftChild;
struct TreeNode* rightChild;
}TreeNode;
TreeNode* CreatTree(char* arr, int* pi)
{
if(arr[*pi] == '#') {
(*pi)++;
return NULL;
}
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
assert(root);
root->data = arr[(*pi)++];
root->leftChild = CreatTree(arr, pi);
root->rightChild = CreatTree(arr, pi);
return root;
}
void InOrder(TreeNode* root)
{
if(root == NULL) {
return;
}
InOrder(root->leftChild);
printf("%c ", root->data);
InOrder(root->rightChild);
}
int main()
{
char str[100] = { 0 };
scanf("%s", str);
int i = 0;
TreeNode* root = CreatTree(str, &i);
InOrder(root);
printf("n");
return 0;
}二叉树的销毁
为了避免销毁二叉树时造成结点丢失造成野指针或非法访问的情况,我们使用后序遍历销毁,先销毁根节点的左、右子树,最后释放根节点。
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.e1idc.net

