前言
此文章是关于时间复杂度的
提示:以下是本篇文章正文内容,下面案例可供参考
一、时间复杂度是什么?
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
大白话来说就是:这个算法最高跑了多少次。不懂?没关系,下面我们看具体例子,每个例子都有他的特色,可能会打断你上一条的想法,然后你就明白时间复杂度是个什么东西。
二、实体展示
1.时间复杂度为1
void Func4(int N) {
int count = 0;
for (int k = 0; k 时间复杂度为1,是执行常数次的意思,CPU一秒能运行上亿次,这些数字不过尔尔,你的int又能有多大。
所以这里虽然运行100次,但是时间复杂度为1。
2.时间复杂度为N^2
代码如下(示例):
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N) {
int count = 0;
for (int i = 0; i Func1 执行的基本操作次数 :
F(N)=N^2+2*N+10;实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法(这个就是取最高阶的)。
这里我们就取N^2。
3.时间复杂度还是为N^2
void BubbleSort(int* a, int n) {
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}我们来看最坏执行了N*(N+1)/2,最高阶是多少是N^2,其他的1/2,N/2,统统不要了。
4.时间复杂度为M+N
代码如下(示例):
void Func3(int N, int M) {
int count = 0;
for (int k = 0; k 因为M和N不是一个未知数,所以不能合并,是不是又认知到了什么。
5.时间复杂度为N
void Func2(int N) {
int count = 0;
for (int k = 0; k 看清楚了M是10,不是未知数。
6.时间复杂度为logN
int BinarySearch(int* a, int n, int x) {
assert(a);
int begin = 0;
int end = n-1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin >1);
if (a[mid] x)
end = mid-1;
else
return mid;
}
return -1; }这个代码是数学上二分法的实现,就不停得除二,执行多少次呢,log2(N),所以这类的时间复杂度为logN。
三、总结
这么看来时间复杂度就那么几个式子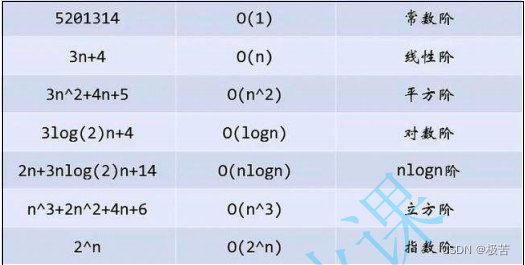
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net

