第十四章 其它曲线（Miscellaneous Curves）

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

译者：池中物王二狗(sheldon)

blog: http://cnblogs.com/willian/

源码：github: https://github.com/willian12345/coding-curves

曲线艺术编程系列 第十四章

这是系列文章规划的最后一章。如果后面发现其它有趣的曲线类型可能加在这一章。我原计划清单里有几个主题没放出来，当然也不排除某天我改主意了。未来额外的内容也可能另起一章加到目录索引中。

在“最后”一篇， 我想我会讲一些随机曲线，这些曲线不值得单独开一章来讲。还有，我觉得把我从找到公式到编码的过程完整过一遍会很不错。

大麻曲线

Weisstein, Eric W “大麻曲线” 来源于网站 https://mathworld.wolfram.com/CannabisCurve.html

Wolfram Mathworld 是一个很好的发掘有趣公式的地方，顺便说一句，如果你想发掘更多 2d 曲线，那么在平面曲线（Plane Curve）这一章节可以深入找找。网站内容很全，还有其它曲线类型可探索。

为什么选择大麻曲线？。我只是觉得它很酷（译者注：本人在此申明我与赌毒不共戴天），仅仅用简单的相关地数学公式就可以画出如此复杂的东西。

下面是对应的数学公式：

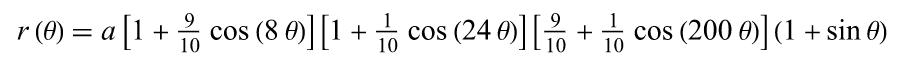
好的，公式有点儿长，但它只是乘法，加法还有一些正弦和余弦计算。我们可以的。

它定义了一条极坐标曲线，这意味着相比于 x, y 的值，我们更关心角度与半径。我们有个函数 r(θ), θ 是希腊字母，theta。它通常代表角度。当然我们也能猜到 r 代表半径。所以我们需要一个函数传入角度得到对应的半径。

有了角度和半径，我们很容易计算出用于绘制线段的 x,y 点。组织代码后应该像下面在这样：

for (t = 0; t 

我们通过 t 计算得到半径，然后再通过半径和 t 计算得到下一个绘制线条的坐标点。

不过事实上来讲，r(θ) 除了在这个循环内不会在其它任何地方使用，我就直接硬编码了。

此处唯一额外要说明的就是需要传入参数 radius 用 radius 乘以公式。还需要用 x, y 让曲线居于中心点，所以我们也把它作为参数传递（xc 与 yc 代表 x 和 y 中点）。

（译者注：这里原作都在 r(t) 计算时用字母小 a 指代除公式之外的部分, 我觉得更难理解更麻烦，小 a 在英语中随处可见，又不在伪代码中明确标出，所以我决定去掉。直接用中文表达出作者原本的意图）

以下面代码作为起点：

function cannabis(xc, yc, radius) {
  for (t = 0; t 

现在，我们在上面基础上进行编码。相当的简单，我们只需代入公式。分数部分我们使用 0.1 代替 1/10, 0.9 代替 9/10。开始吧！

function cannabis(xc, yc, radius) {
  for (t = 0; t 

现在，像下面代码这样看看：

canvas(600, 600)
cannabis(300, 300, 140)
stroke()

That gives me this image:

这会得到如下图：

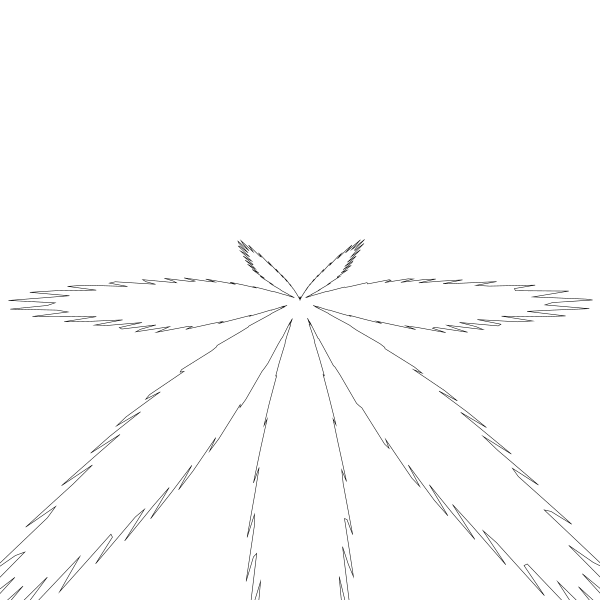
Ah, 好的，有点儿东西。

首先，此公式使用笛卡尔坐标系，而我用的是上下相反的屏幕坐标系。所以我需要把 y 轴翻转。问题不大。

接着，中心点是所有“叶子”连接点。所以在翻转后，我可以将中心点设置在 canvas 靠近底部的位置。

最后，我猜 140 会是一个不错的半径值，它会将绘制出的图形限制在 600X600 大小的 canvas 内。事实上，我期望的是把图形限制在 canvas 大小的一半。但实际上大的叶子超出一部分也不影响。我们可以在代码中修复它，比如将半径乘以某些小数让大的叶子半径降下来。我就不做这部分限制了，我假装自己只会传合适的值，相关限制代码你自己可以搞定的。

function cannabis(xc, yc, radius) {
  for (t = 0; t 

我所做的只是将 lineTo 这一行用yc + y 代替了 yc - y 。

在调用函数时参数也调整了一下（经过试错后得出还不错的参数值）

canvas(600, 600)
cannabis(300, 520, 120)
stroke()

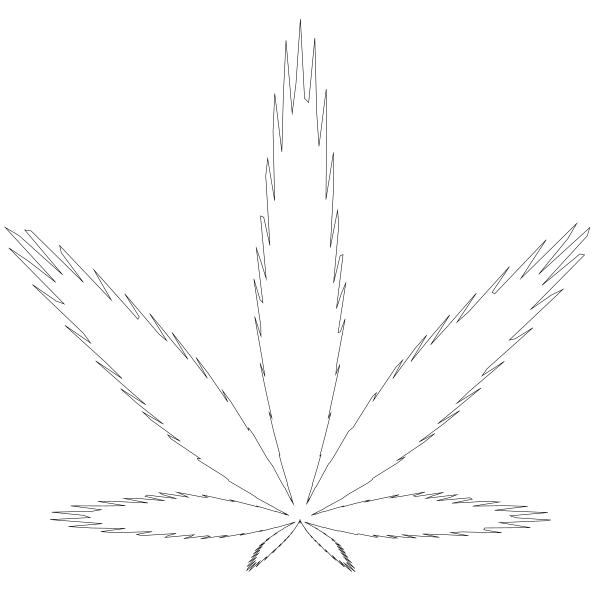
结果还阔以！

提醒一下。我经过仔细考虑调整了 canvas 的大小，这样 yc 参数值可以设置到 420。 你调不调的隨你🙂。

当然，现在我很好奇这个公式到底做了些什么。 radius * 后面分 4 部分，圆括号内分别有 — 三个 余弦 cos， 一个正弦 sin。第一个括号内直接写了数值（硬编码） 8 。

... (1 + 0.9 * cos(8 * t)) ...

自从设了值为 8 便有了 7 片可见的叶子，我猜它们之间有联系 – 它实际上有可能有 8 片叶子，只是最底部的那一片太小，我们看不到。 我将 8 调高到 12 …

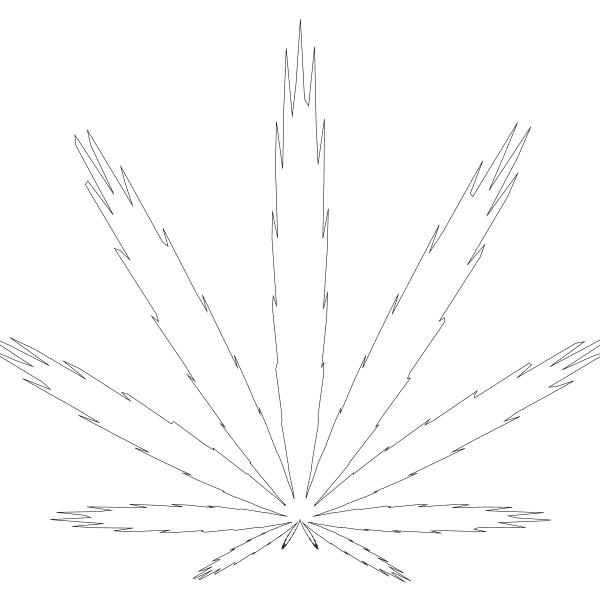
你看看！理论验证成功。 7 片可见叶子加上一片不可见的。

在第二部分数 24 的作用就不太容易看出来。

... (1 + 0.1 * cos(24 * t)) ...

如果把代码回调然后把数值 24 设为 0 ，叶子边缘会非常圆润。

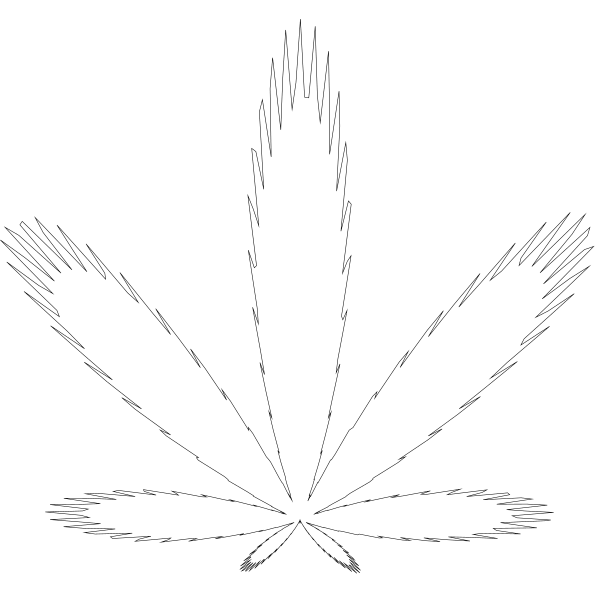
调到 24 一倍至 48 会得到：

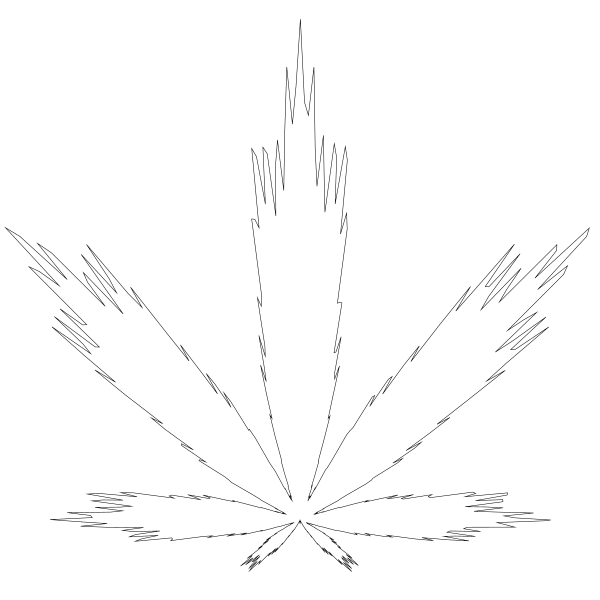
这结果有点儿像每片叶子上又生出了三片小叶子。让我们把值改回 24 然后改变乘数：

... (0.7 + 0.3 * cos(24 * t)) ...

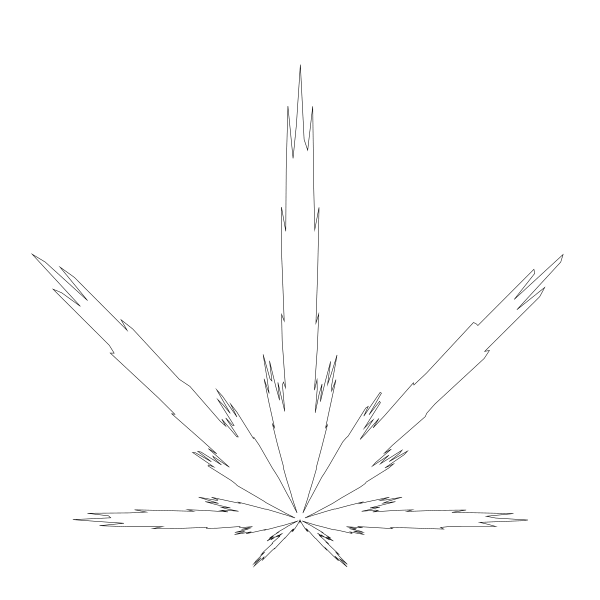
还是看到三片小叶子，24 = 8 * 3 很合理。所以这部分使用非常小的乘数， 0.1, 来微调每片叶子 – 让它变的不那么圆润。酷。把代码调回原位后再往下看另一部分。

... (0.9 + 0.1 * cos(200 * t)) ...

数值 200 我猜是用来创建锯齿边的。如果我把它 改为 100 ， 锯齿变就变少了。

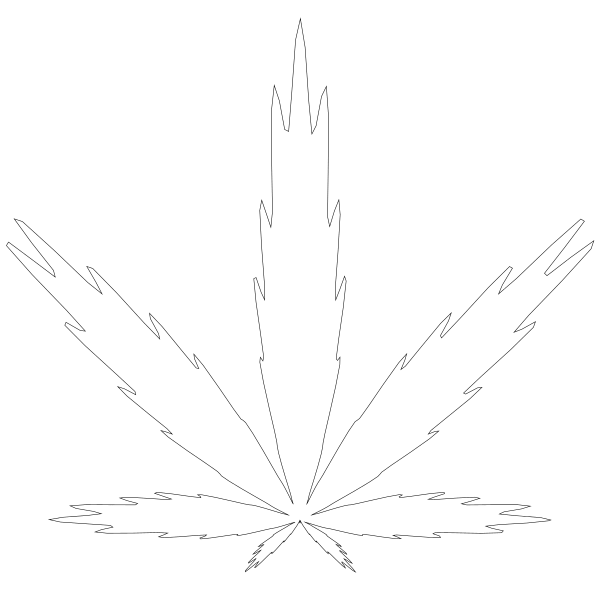
但现在看起来块儿状化了。试着增加分辨率把 for 循环从 0.01 调至 0.005:

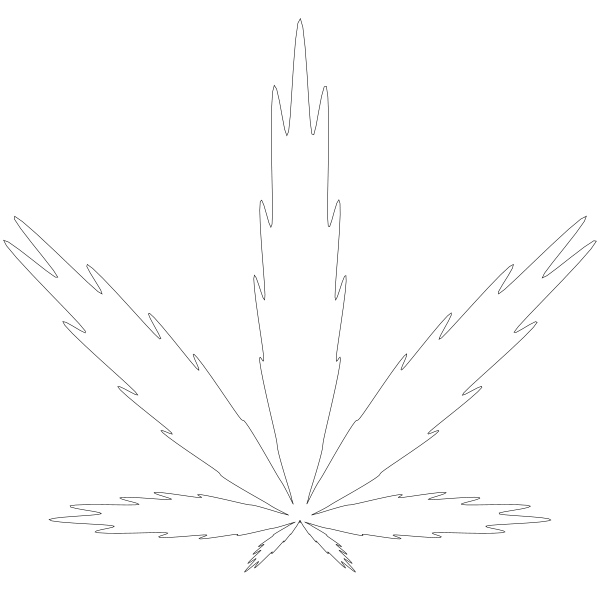
Mmmm… 丝滑。

反代码复原后再看最后一个 sin 的作用。

... (1 + sin(t))

我一开始猜它影响的是曲线的朝向。我想如果把这部分删掉，叶子可能会朝向一边。但我发现我猜错了。下面是我移掉这部分代码并将 yc 调回到 canvas 中心点 300 后的结果：

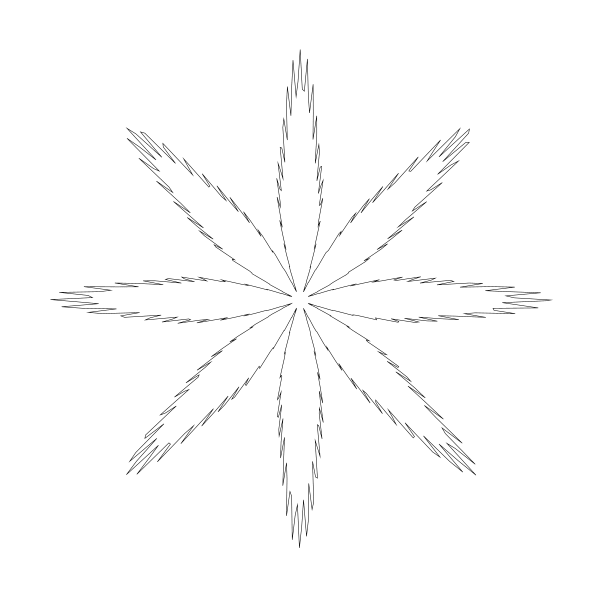
真是个小惊喜！在这个基础上我的点子可就多了，另外那消失的第 8 片叶子也找到了！

心形

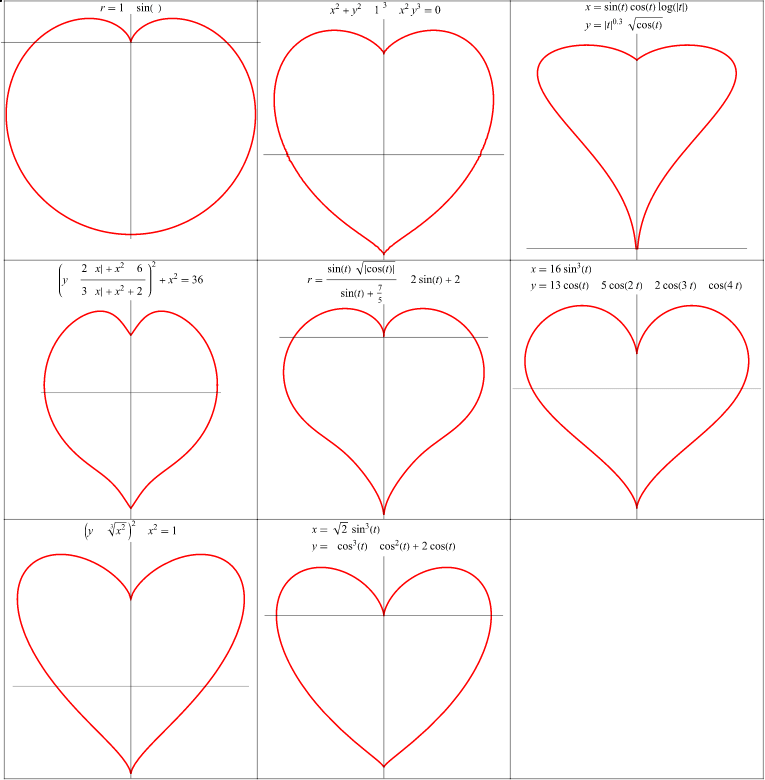
Weisstein, Eric W. “Heart Curve.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/HeartCurve.html

再一次，还得靠 Mathworld。如你所见，没有一个单独的公式可以绘制心形曲线。此页展示了 8 种不同的绘制方法。个人来讲我喜欢倒数第二行的最后一个。

相比于上一次接触的极坐标公式（还有其中其它的例子）， 此公式直接给出计算 x 和 y 值。当然还是得用 0 到 2*PI 循环出 t 值。

公式计算 y 坐标，有四个不同的计算部分。不太清楚四个计算合在一起的作用，但如果往下继续看，你会想着删减它们。我关心的还有两点，硬编码的数值太多还有就是没有直接改变心形大小的参数。但我肯定我们可以解决。

来吧，这是非常直接的公式，我们直接进入代码环节用代码写出来。

function heart(xc, yc) {
  for (t = 0; t 

We can run this like so:

像下面这样调用：

canvas(600, 600)
heart(300, 300)
stroke()

And we’ll get:

得到结果：

基本正确，只是需要把它翻转过来，还有就是需要允许调整大小。现在大约宽度是 32 像素。这是硬编码值 16，乘以 2 倍。

翻转就很简单了再次将使用 yc – y

至于尺寸大小，先把硬编码的数值分别除以 16。

x = pow(sin(t), 3)
y = 0.8125 * cos(t) - 0.3125 * cos(2 * t) - 0.125 * cos(3 * t) - 0.0625 * cos(4 * t)

像这样处理后，我们得到的是 2 像素宽度的（1 * 2）心形（译都注：x 轴系数16/16归 1 了，原来 16 是 32 像素意味着输出的图像 1 就是 2 像素）。现在我们可以为它添加控制大小参数 size 了。

function heart(xc, yc, size) {
  for (t = 0; t 

现在像下面这样调用：

canvas(600, 600)
heart(300, 300, 280)
stroke()

得到的结果：

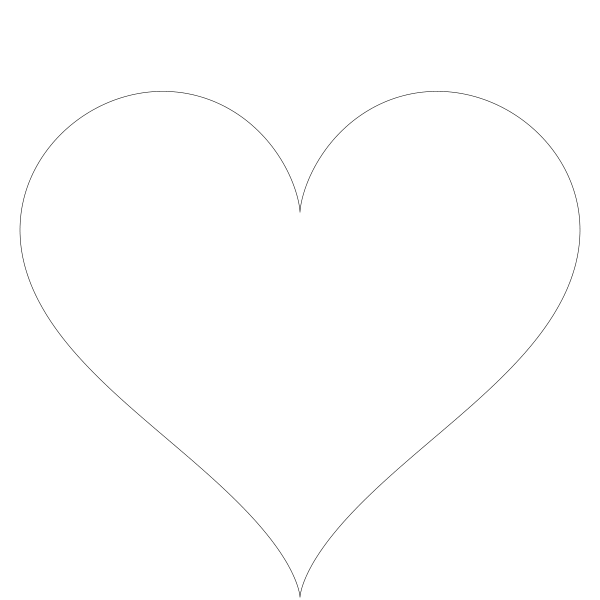
不是很难。

我不打算再深入另外的心形的公式了，相信你自己可以探索，你只需改动其中的常数值看看会发生什么变化。你有更好的方式吗？完全不同的那种？

蛋（卵形）

几年前我才首次接触如何绘制蛋形。此篇中只展示结果，但没有写思考过程。这篇比较完整 https://www.bit-101.com/blog/2021/06/how-to-draw-an-egg/

公式是从这里找到的 http://www.mathematische-basteleien.de/eggcurves.htm

事实上这里有超多的绘制蛋形的公式。就像心形曲线一样，我好奇的是没有一个单独的绘制蛋形曲线的标准公式。

但我把目标锁定在了 “From the Oval to the Egg Shape” 这一章节。此处有一个通用的蛋形或椭圆形公式，y 轴半径在每个点上都是变化的。如果 x 偏右，则 y 值变大，如果 x 偏左则 y 值编小。很直观。

所以我们先从椭圆公式开始，椭圆公式在第三章中我们已经讲解过了。

function ellipse(x, y, rx, ry) {
  res = 4.0 / max(rx, ry)
  for (t = 0; t 

公式很好很简洁，但我得把三角函数部分代码提出来方便对它进行平衡与缩放。为了简洁的解释我还把 res 变量去掉了直接硬编码为 0.01， 当然你可以选择保留它。

function egg(xc, yc, rx, ry) {
  for (t = 0; t 

就是画了个椭圆，只是先确定改动代码有没有错误。

canvas(600, 600)
egg(300, 300, 280, 190)
stroke()

Yup，结果正是个椭圆。数值 280 和 190 是怎么来的？嗯，280 就是比 canvas 宽度一半还小一点点，rx。 ry 也是类似，不断试错后得到 190 这个看起来不错的值。

现在让我们把椭圆变成蛋形。那个网页中给了我们三个公式：

t1(x) = 1 + 0.2 * x
 
t2(x) = 1 / (1 - 0.2 * x)
 
t3(x) = e^(0.2 * x)

这些 t 函数是用来乘以 y 的。我就不再创建新函数了。就在 for 循环中直接乘。先从第一个 t 公式开始…

function egg(xc, yc, rx, ry) {
  for (t = 0; t 

Woo! 得到了一个蛋！

现在我们可以调调公式内的参数了。先从 0.2 这个数值入手。把它设为 0.3 试试。

好的，它看起变的有点儿尖。改为 0.5?

更尖了。懂了哈。把值改回 0.1。

几乎与原椭圆别无二至。这说得通，如果值为 0， 那么这一行啥也没做，它就是个椭圆。让我们把它改回 0.2， 让它变成通常常见的蛋型，再把 ry 改成 220：

一个漂亮“肥”蛋。下面是 150：

我坚持我的数值 190 ，但小调一点也可能更好。多试试吧。让我们再试试其它公式。首先把 ry 调回 190。把公式换成：

y *= 1 / (1 - 0.2*x)

得到：

再试试第三个公式

y *= exp(0.2 * x)

还记得第五章提到过大部分数学库都会提供 exp 函数即 e^x ( e 的“参数”次幂)。这个公式就是调用了 exp 函数，结果如：

由于三个公式看起来都很像，所以我把它们用红绿蓝三种不同颜色都画了出来…

Yeah, 三个几乎相同。可能有几个像素的区别。让我们回头看原网站，它们讨论的是另一种不同的椭圆公式，并且让 y2 乘以 此公式的值：

另一种椭圆公式 x²/9+y²/4=1 变化至 x²/9+y²/4*t(x)=1

除数 9 和 4 依然是硬编码。如果对它们开方得到 3 和 2。而 280 的 2/3 刚好是 186（译者注：公式简化后可观察得到 ry 是 2/3 的 rx）。 所以之前我选择 ry 为 190 挺合理的！

无论如何，我们有了可以画出令人信服的蛋形公式，无论使用哪种算法。就到这儿吧。这就是我写文章的过程，当然我写代码也是类似的思考，你完整的了解了整个过程，去掉了一些源文中的细枝末节。但得到的结果依然相当不错！

（译者注：很多情况下你不需要知道公式的完整推导过程，人生苦短直接使用公式即可）

小结

如何从不同地方找到各种公式把它们转变成代码绘制出有趣的图形, 希望这会给你一些启发 – 如果你从未做过的话。

我把它们全部归档到了 coding curves 系列中。至少现在为止是这样。不过我想到了另一个系列，关注我不迷路！

---

博客园: http://cnblogs.com/willian/
github: https://github.com/willian12345/

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.fwqtg.net