
背景
知识图谱系统的建设需要工程和算法的紧密配合,在工程层面,去年蚂蚁集团联合OpenKG开放知识图谱社区,共同发布了工业级知识图谱语义标准OpenSPG并开源;算法层面,蚂蚁从知识融合,知识推理,图谱应用等维度不断推进。
OpenSPG GitHub,欢迎大家Star关注~:https://github.com/OpenSPG/openspg
本文将梳理知识图谱常用的推理算法,并讨论各个算法之间的差异、联系、应用范围和优缺点,为建设知识图谱的图谱计算和推理能力理清思路,为希望了解或者工作中需要用到知识图谱推理算法的同学提供概述和引导。本文为上篇,将主要从“基于距离的翻译模型”,“基于图传播的模型”两大板块进行介绍。
知识图谱算法汇总
本章将对常用的图谱推理算法做一个概括的梳理。业界算法很多,一篇文章难以做到全面覆盖,因此我们这里挑选了与图谱推理强相关的算法进行讲解,部分类似的算法挑选了其典型代表进行讨论,算法能力范围尽量覆盖:
-
知识融合,包括:实体对齐、属性融合、关系发掘、相似性属性补全;
-
知识推理,包括:链接预测、属性值预测、事件分析、连通性分析、相似性分析。
首先,通过一张思维导图对这些图推理算法进行汇总:
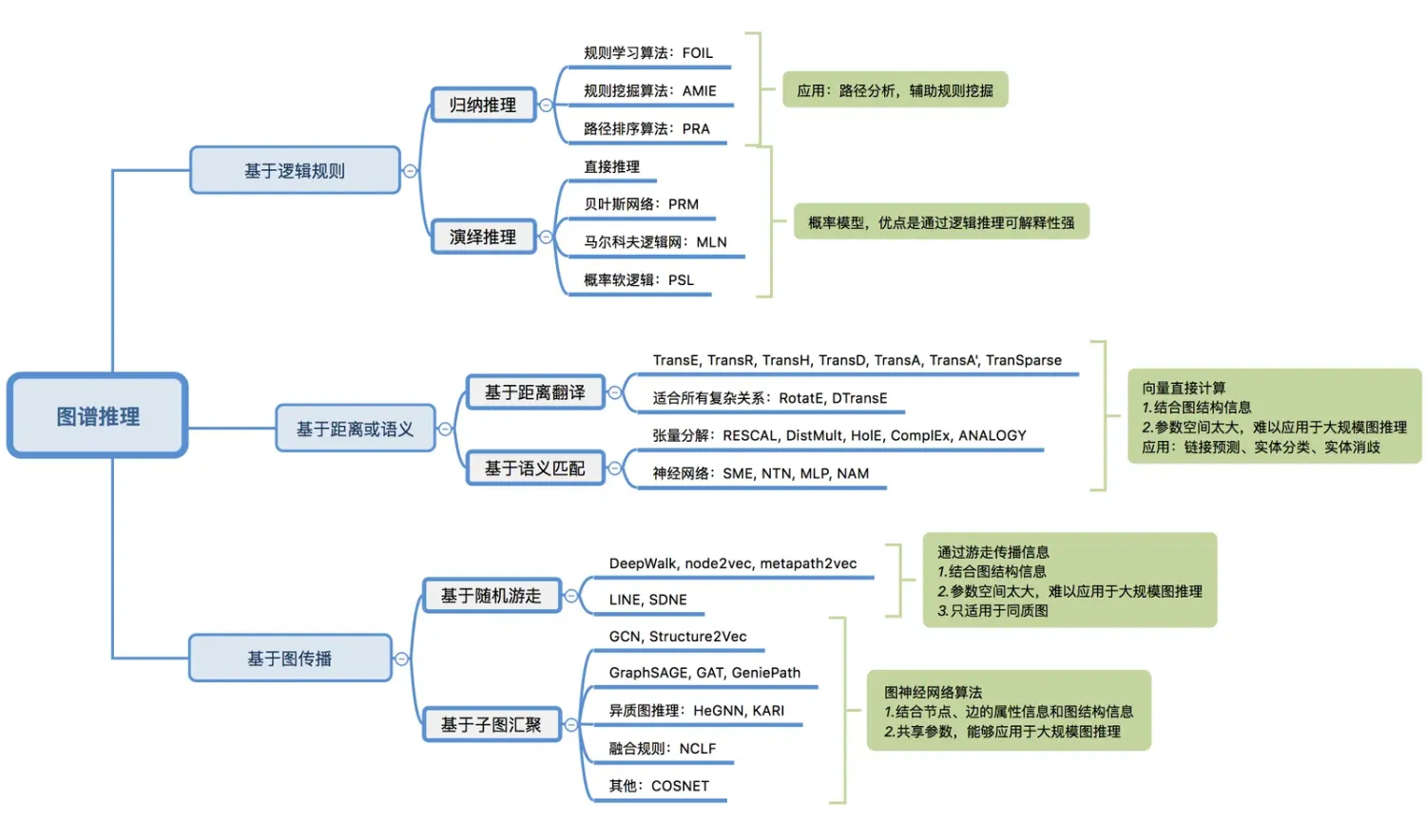
01:符号推理:基于逻辑规则的推理
-
归纳推理算法,用于规则挖掘
a.归纳程序:FOIL规则学习算法,根据增加例子的正、反例数目,计算Foil_Gain因子,选其最大的作为新增规则。
b.关联规则挖掘:AMIE规则挖掘算法。目标是生成边关系规则,事先依据边类型生成所有可能的规则,再在图谱中找出支持该规则的事实,置信度达到阈值则认为该规则成立。缺点:数据稀疏时很难实用。
c.路径排序算法:PRA路径排序算法 (Path Ranking Algorithm)。该算法将每条不同路径的概率作为特征,其中路径概率等于该路径上每步游走的联合概率。然后用逻辑回归分类器做训练和预测,其训练语料为两点之间的各条路径的概率。模型的预测结果包含分类结果以及各条路径的权重,后者可以用作结果解释以及辅助规则挖掘。缺点:这种基于关系的同现统计的方法,都面临数据稀疏时难以实用的问题。PRA的后续改进算法有带采样策略的SFE,多任务耦合的CPRA,效果均有提升。
-
演绎推理算法,用于规则挖掘、事件推理
a.基于规则的直接推理。只适用于确定性推理,不能进行不确定性推理。比如 marryTo(A,B) -> marryTo(B,A)。
b.基于贝叶斯网络的概率关系模型(Probabilistic Relational Models),用条件概率表示因果关系,形成图结构。
c.马尔可夫逻辑网(Markov Logic Network)是将概率图模型与一阶谓词逻辑相结合的一种统计关系学习模型,其核心思想是通过为规则绑定权重的方式将一阶谓词逻辑规则中的硬性约束进行软化。即以前的一阶谓词规则是不能违反的,现在采用了概率来描述。其中,权重反映其约束强度。规则的权重越大,其约束能力越强,当规则的权重设置为无穷大时,其退化为硬性规则。该模型的事实的真值取值0或者1,模型可以学习规则(结构学习),学习权重,利用规则和权重推断未知事实成立的概率。
d.概率软逻辑(Probabilistic Soft Logic)。是马尔可夫逻辑网的升级版本,最大的不同是事实的真值可以在[0,1]区间任意取值。进一步增强了马尔可夫逻辑网的不确定性处理能力,能够同时建模不确定性的规则和事实。并且连续真值的引入使得推理从原本的离散优化问题简化为连续优化问题,大大提升了推理效率。因为是连续值,所以其“与、或、非”规则专门定义了一套公式。
02:数值推理:基于图表示学习的推理
图表示学习(Knowledge Graph Embedding)是知识图谱中的实体和关系通过学习得到一个低维向量,同时保持图中原有的结构或语义信息。所以一组好的实体向量可以充分、完全地表示实体之间的相互关系,因为绝大部分机器学习算法都可以很方便地处理低维向量输入,可以应用于链接预测、分类任务、属性值计算、相似度计算等大多数常见任务。
基于距离的翻译模型
这类模型使用基于距离的评分函数评估三元组的概率,将尾节点视为头结点和关系翻译得到的结果。这类方法的代表有TransE、TransH、TransR等;
TransE模型无法很好地建模“自反/多对一/一对多”型关系。解决方案一:允许同一实体在不同关系下有不同的表示比如:TransH、TransR。解决方案二:放松实体和关系间的位移假设,比如TransM,TransF,ManifoldE。
基于语义的匹配模型
这类模型使用基于相似度的评分函数评估三元组的概率,将实体和关系映射到隐语义空间中进行相似度度量。这类方法分为两种:一类是简单匹配模型:RESCAL张量分解模型及其变种。二类是深度神经网络SME、NTN(Neural Tensor Networks)神经张量模型、MLP、NAM等等。
基于图传播的模型
该类模型将图看做节点以及与节点连接的边。信息在图上进行传播。模型一般分两类:
-
基于随机游走的图传播模型:node2vec、Deepwalk、LINE、metapath2vec等
-
基于子图汇聚的图传播模型:GCN、Structure2Vec、GAT、GeniePath、KARI、COSNET等
算法详细梳理
01:基于距离的翻译模型
这类模型使用基于距离的得分函数评估三元组的概率,将尾节点视为头结点和关系翻译得到的结果。
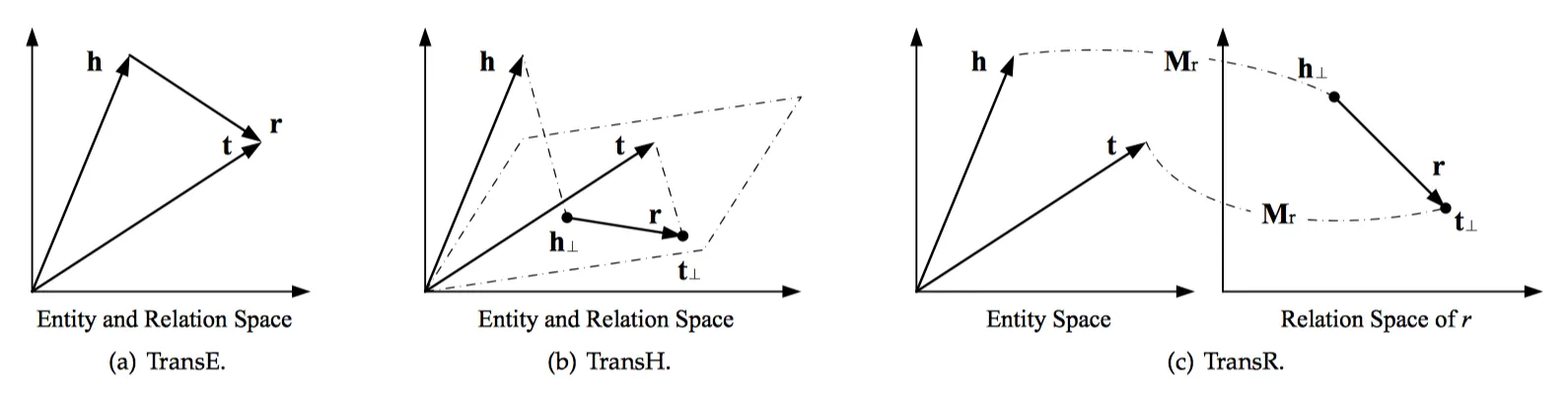
TransE
TransE[6]是将实体与关系表示为低维向量的简单模型。该模型已经成为了默认的知识图谱向量化表示的baseline,并衍生出不同的变体。TransE关注头向量h加上关系向量r与尾向量t之间的距离,并以此为优化目标。最终通过学习得到每个节点和关系的嵌入向量(Embedding)。下面一系列算法的训练过程与此类似就不再重复。
距离得分公式为:

TransE模型因为太简单,在给定任意两个向量的情况下第三个向量基本就固定了,因此面对1-N, N-1, N-N问题会得到N个相近的嵌入向量,此外遇到对称关系会得到r=0,导致对这些问题处理不太理想。因此后续工作在TransE的基础上提出了TransR、TransH等模型,很好的解决了1-N, N-1, N-N问题。
TransR
TransR[7]中每一种关系r都有一个映射矩阵Mr,这样不同的关系就可以在不同的映射空间计算距离得分。

距离得分公式:

TransH
TransH[8]继承了TransR的思想,但做了简化,用一个映射平面(投影平面)的法向量wr来代替映射矩阵Mr。这样使得参数空间大大减小。

这里解释为什么TransH能够解决1-N, N-1, N-N问题,TransR等算法类似。TransE的问题是三元组中任意两个向量被固定以后,第三个向量就没有了自由度,因此训练得到的嵌入向量在空间上就很接近。而TransH就不会有这样的问题。如下图所示,头向量h与尾向量t都会投影到特定关系对应的投影平面上,那么在投影平面法线(虚线)任意位置处的头向量和尾向量都可能成为潜在的头向量h与尾向量t(蓝色箭头所示)。这里h、t就有了一个自由度,该自由度保证了TransH不会像TransE那样在给定任意两个向量时总是将第三个向量指向同一位置,因此就较好的解决了1-N, N-1, N-N问题。在增加额外自由度这一方面transH、transR、transD等模型都能办到。
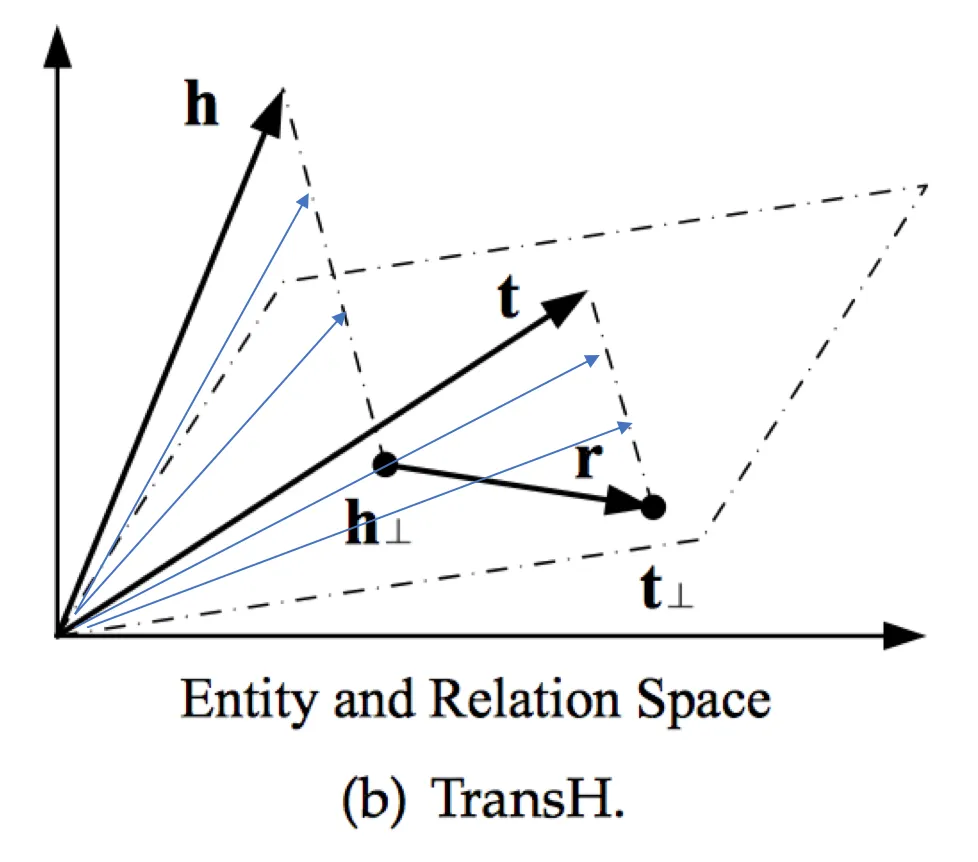
TransH距离得分公式

TransD
TransD[9]在TransH上做了一点小小的改动,让不同的头向量和尾向量也多了各自的映射空间。


距离得分公式:

TranSparse
TranSparse[10]是在TransR的基础上,将不同的数据稀疏程度信息考虑到了映射矩阵中来了。
 . 针对h, t的转换矩阵相同
. 针对h, t的转换矩阵相同
 . 针对h, t的转换矩阵不同
. 针对h, t的转换矩阵不同
距离得分公式:

TransA
前面的那些trans方法平等对待向量中的每一维,但实际上各个维度的重要性是不同的,只有一些维度是有效的,而某些维度被认为是噪音,会降低效果。TransA[11]模型通过引入加权矩阵,赋给每一维度权重。从空间上来看,相当于选择空间从圆变成了椭圆。
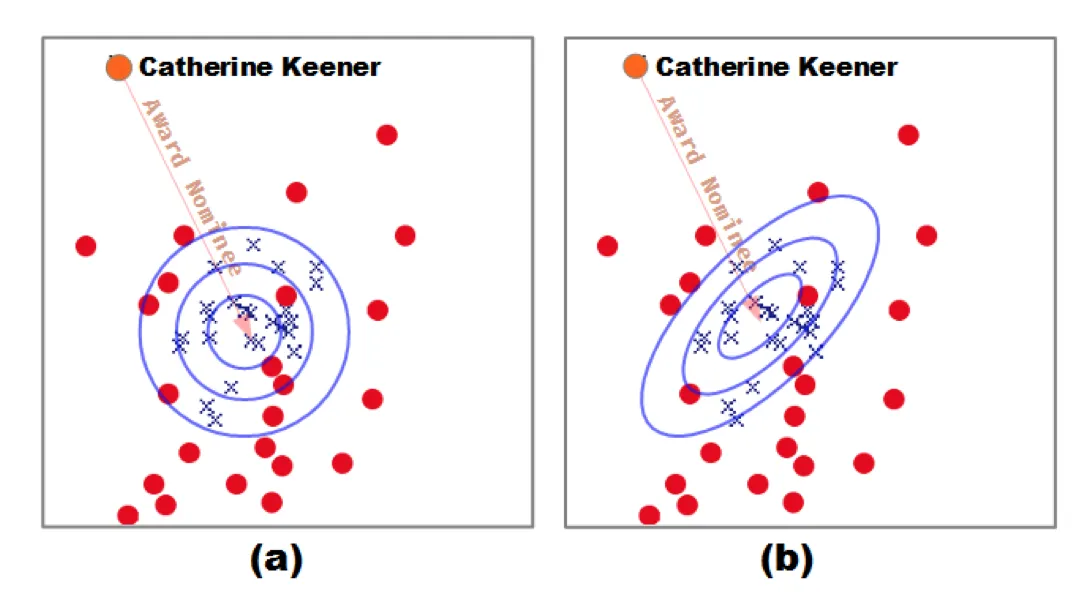
TransA引入了 矩阵为不同维度的向量进行加权,并利用LDL方法对
矩阵为不同维度的向量进行加权,并利用LDL方法对 进行分解,
进行分解, 是一个对角阵,对角线上的元素表示不同维度上的权重。本篇文章的一个亮点在于通过图像来描述不同的损失度量函数,给人直观的感觉。
是一个对角阵,对角线上的元素表示不同维度上的权重。本篇文章的一个亮点在于通过图像来描述不同的损失度量函数,给人直观的感觉。

TransA’
TransA’[12]可以通过学习获得自适应的margin。Trans系列算法的loss如下,其含义是将事实三元组和负采样三元组从距离上尽量分开。

其中 是给定常数的margin,用于将正、负三元组分开。margin越大将容许越多的错误三元组(即f(h,r,t)大于f(h’,r’,t’)的三元组)被计入loss计算中,这将会导致模型容易过拟合;相反,margin 越小越容易排除掉很多正、负样本距离得分相近的数据(即f(h,r,t)与f(h’,r’,t’)接近的三元组),容易欠拟合。
是给定常数的margin,用于将正、负三元组分开。margin越大将容许越多的错误三元组(即f(h,r,t)大于f(h’,r’,t’)的三元组)被计入loss计算中,这将会导致模型容易过拟合;相反,margin 越小越容易排除掉很多正、负样本距离得分相近的数据(即f(h,r,t)与f(h’,r’,t’)接近的三元组),容易欠拟合。
之前的trans模型的 margin 都是固定不变的,但不同的 margin 是否能够提升模型的效果呢?TransA’[12]为了证明该效果,将 margin 分为 entity 和 relation 两部分,并利用线性插值进行组合。实体部分的 margin 应保证内层圆包含更多的正例(用圆圈表示),外层圆的外部应尽可能是负例(用方块表示)。对于 relation 部分,TransA’利用 relation 的长度,即 L2 范式来衡量相似度关系。具体公式如下图所示:

文章中的实验表明,采用自适应的margin以后,效果有明显提升(MR有明显提升)。
RotatE
1). 原理
RotatE[13]将实体和关系映射到复数向量空间,并且将每个关系定义为头实体到尾实体的旋转。RotatE借鉴了欧拉恒等式 。关系
。关系 代表旋转
代表旋转 度,并且
度,并且 。给定三元组 (h,r,t),期望
。给定三元组 (h,r,t),期望 即h通过r旋转后与t相等,其中h,r,t属于C,
即h通过r旋转后与t相等,其中h,r,t属于C,  ,
,  是哈达玛积,则对于复数空间中的每一维都有:
是哈达玛积,则对于复数空间中的每一维都有:

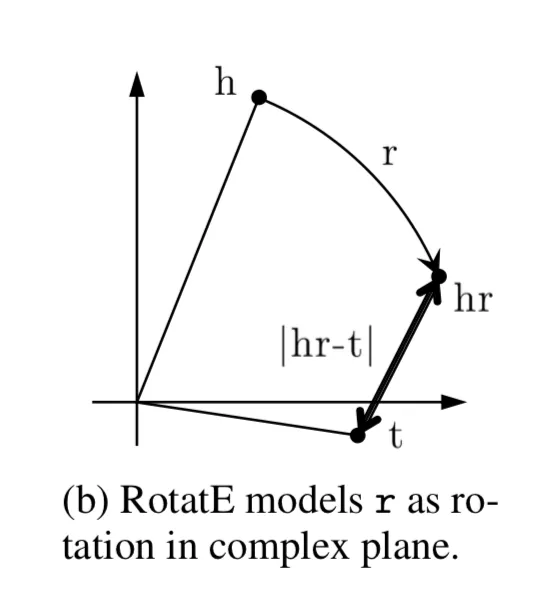
距离函数为:

2). 支持复杂关系
文章提供了另外一个角度来验证不同算法的效果,那就是:对称/非对称、相反、组合。三类关系定义如下:
- 关系 r 是对称/反对称的:if ∀x,y : r(x,y) ⇒ r(y,x) / (r(x,y) ⇒r(y,x));
- 关系 r1 是关系 r2 的反:if ∀x,y : r2(x,y) ⇒ r1(y,x);
- 关系 r1 是关系 r2 和 r3 的组合:if ∀x,y,z : r2(x,y)r3(y,z) ⇒r1(x,z)。
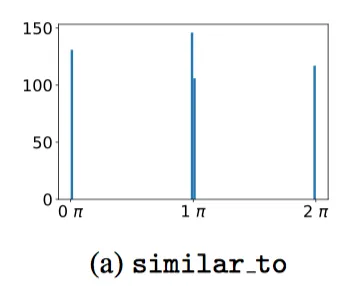
文章还从实验结果上给出了很直观的解释。对于对称关系similar_to,如下图。RotatE大部分情况学到的r对应的 ,也有少部分情况对应
,也有少部分情况对应 (这种r接近0的对称结果也会被学出来,transE专门干这个的)
(这种r接近0的对称结果也会被学出来,transE专门干这个的)
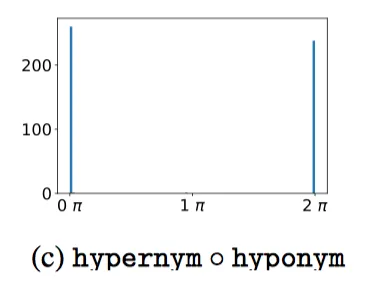
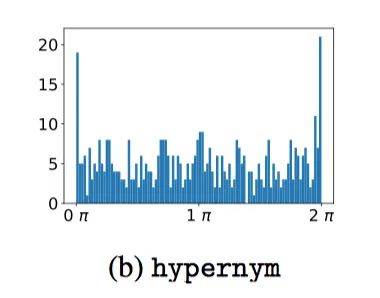
对于相反关系hypernym & hyponym相乘,如下图,对应的正好是整数倍 。
。
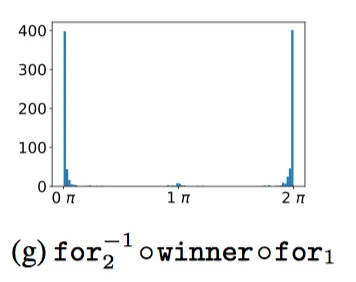
对于组合关系for2-1 & winner & for1,h, r组合以后再减去t,自然也是整数倍 。
。
对于其他普通的情况呢,就分布在各处了。
文章附录中证明了RotatE通过简单的旋转操作可以有效地建模上面所有关系模式。文章也列出了几种常见算法使用哪些模式,见下表。
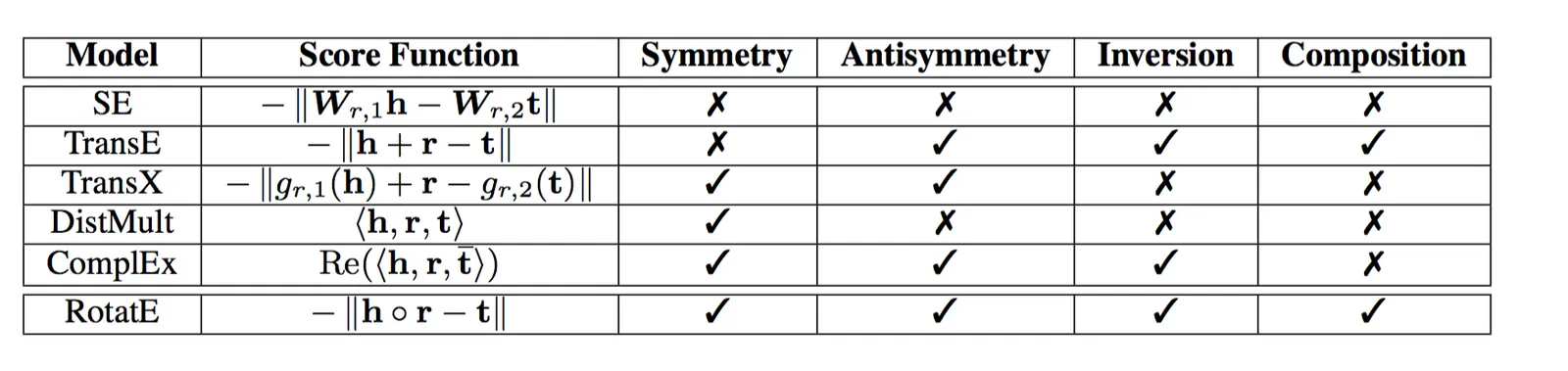
可以看到,在这些算法中,RotatE是唯一能够满足所有模式的模型。其中transX表示一类先将头、尾向量映射,然后再算距离的模型,比如transH、transR。文章中该表格有错误,因为transX也能满足相反关系。以TransH举例,因为TransE能满足相反、组合关系,又因为transH在投影以后和TransE是一样的,因此同样也满足。
为什么RotatE既能够满足对称关系,也能满足非对称关系?因为旋转具有周期性,对称关系等价于两次旋转操作叠加以后回到原点。当一次旋转操作为半个周期,正好就满足该条件。此外,当一次旋转不等于半周期或者周期的倍数时,那么就对应了非对称关系。
为什么TransX既能够满足对称关系,也能满足非对称关系?证明比较容易。结论是TransX自然是满足非对称关系,只需要证明TransX也满足对称关系。以TransH为例:当TransH遇到对称关系时,学到的参数需要满足 且
且 ,因为后者不为零,因此该参数依然可以区分不同的关系。
,因为后者不为零,因此该参数依然可以区分不同的关系。
3). 复杂关系对比实验
- 在FB15k 数据集上,主要的关系模式是对称/反对称和反转
- 在WN18数据集上,主要关系模式是对称/反对称和反转
- 在 FB15k-237 数据集上,主要的关系模式是对称/反对称和组合
- 在 WN18RR 上,主要的关系模式是对称/反对称和组合
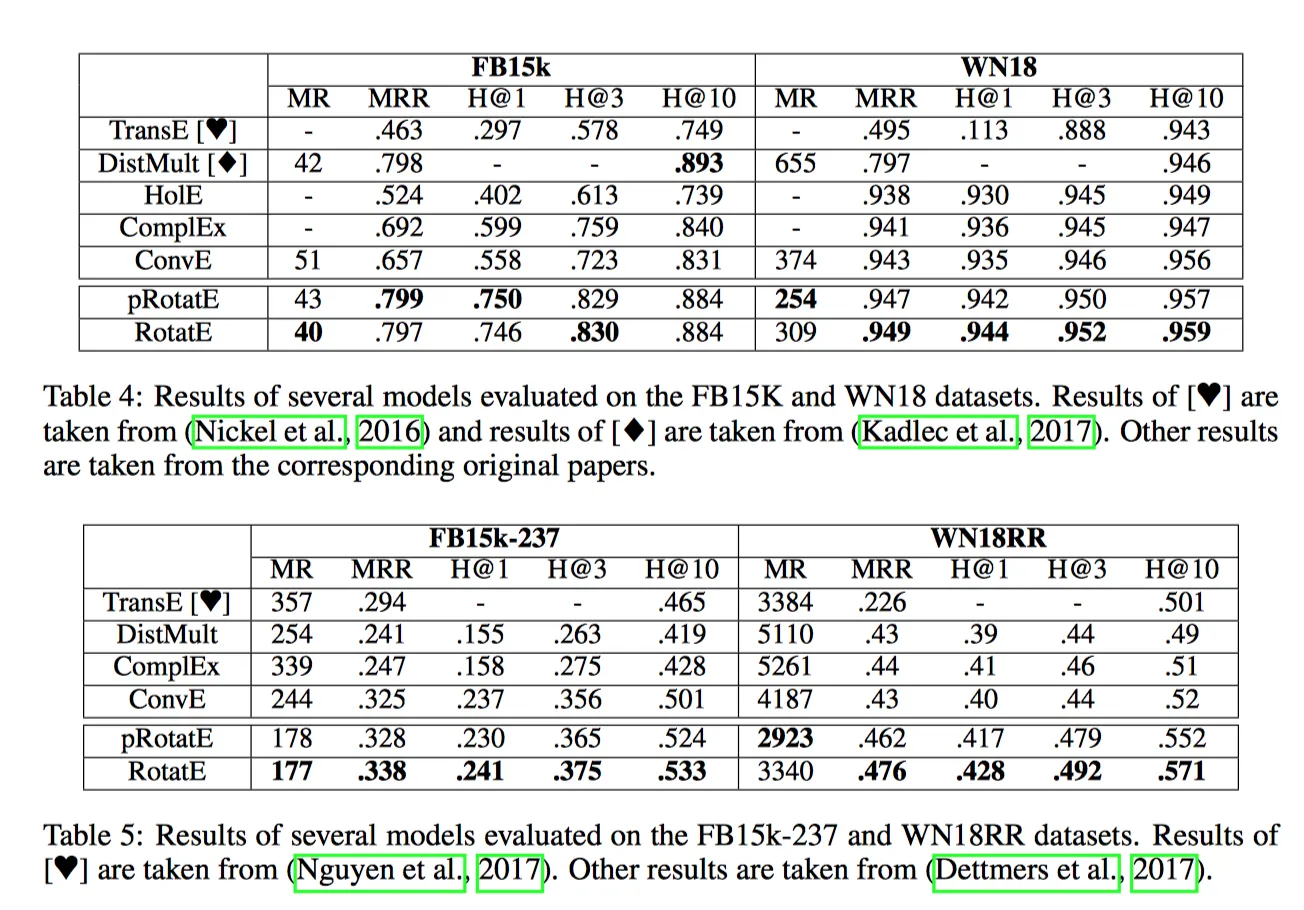
从上表中可以看到,因为不同的模型适用的模式不同,因此在不同的数据集中有不同的表现。TransE不适用于对称关系,所以在四个数据集中表现都差。而ComplEx仅仅不适用于组合关系,因此在上面两个数据集表现好,而在下面两个数据集表现差。RotatE适用于所有关系,所以在四个数据集中表现都好。
4). 自我对抗负采样
本文提出了一种自我对抗负采样(self-adversarial negative sampling)方式,效果不错。传统负采样损失如下.使用统一的方式对待所有三元组,即1/k系数,这种模式会出现问题。因为在训练的过程中,许多样例明显是假的,不能提供任何有意义的信息。

因此对负采样方法进行改进,提出“自我对抗负采样”,根据当前的嵌入模型的打分来采样负例。具体来说,遵循以下分布采样负三元组:

将该分布概率视作负例的权重,因此最终具有自我对抗训练的负采样损失函数如下

注:权重系数最终需要为负,让难以区分的负样本(得分低的)获得更高的权重。
5). 负采样对比实验

从上表中可以看到,TransE用上自我对抗负采样以后,提升明显。
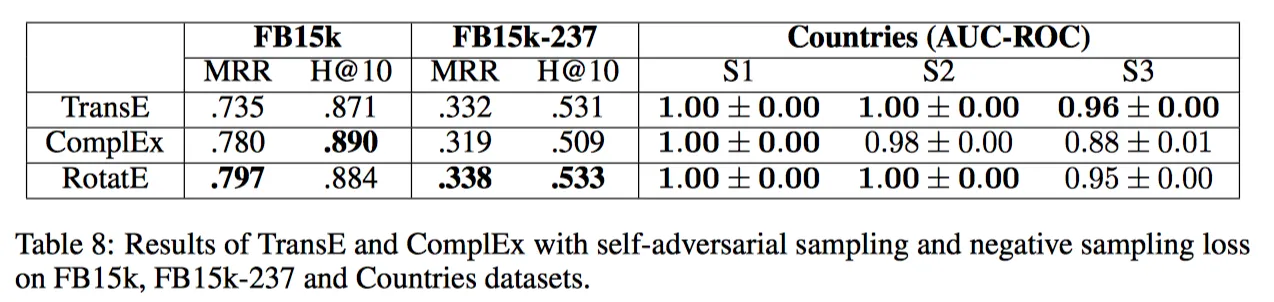
从上表中可以看到,该负采样用到其他模型上效果也不错。这样就显得RotatE优势不那么明显了。
DTransE
DTransE算法是我们知识图谱团队自研的算法,详细内容见本文末的系列ATA文章。该算法融合了语义匹配模型和距离模型,如下图所示。
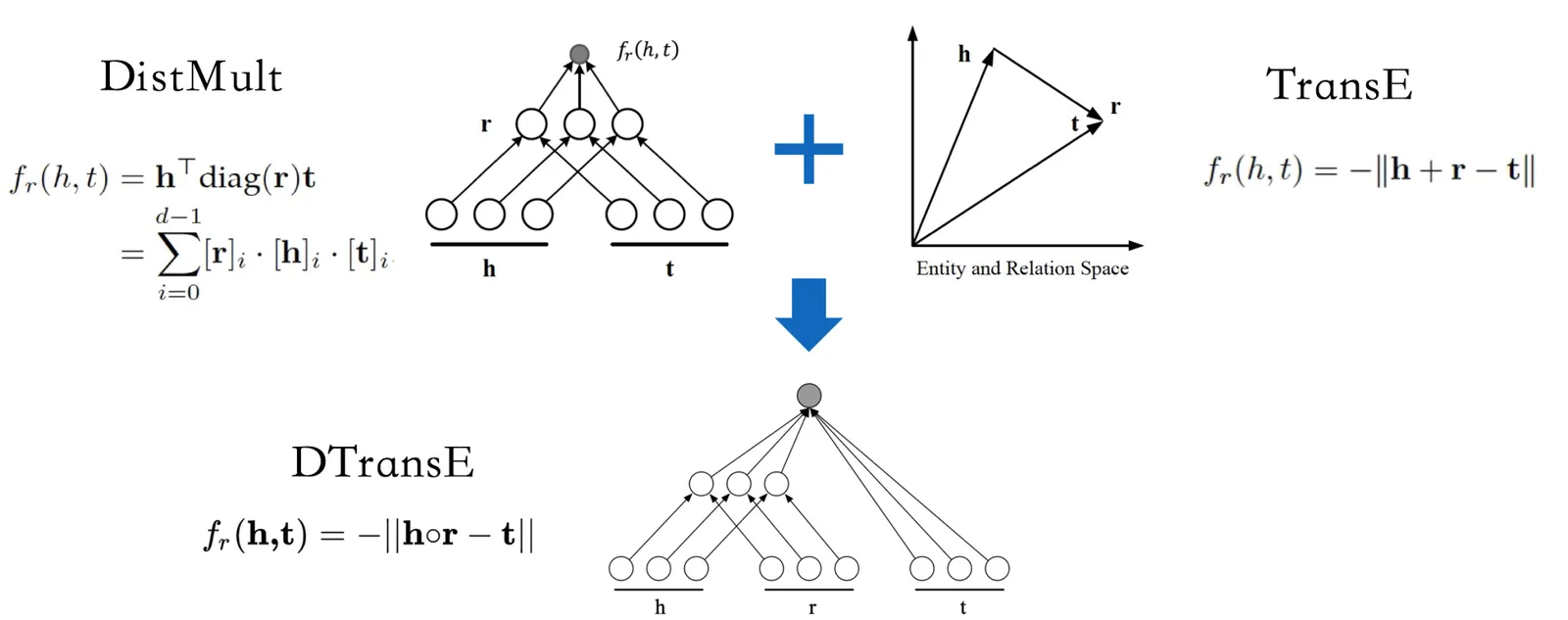
图:DtransE原理示意图
得分函数表达为:

其中 是三元组的打分,h、r、t分别是头节点向量、关系向量、尾节点向量,
是三元组的打分,h、r、t分别是头节点向量、关系向量、尾节点向量, 是按位相乘。DTransE算法具有以下特性:
是按位相乘。DTransE算法具有以下特性:
- 融合了经典语义匹配模型DistMult和经典距离模型TransE
- 不引入复数,在实数空间即可同时支持对称/非对称、反转、组合关系
- 模型大小显著降低,减少计算复杂度,便于业务落地。
效果方面DTransE算法在FB15K-237、WN18、YAGO3-10等多个数据集上达到或持平state-of-art。
Trans系列算法小节:
transH、transD、transR这三个算法在几何变换上是等效的,就是对向量h和t在空间上做了一个变换(包括角度变换和长度伸缩两个操作),不同的关系r对应的变换矩阵不同,还有参数数量不同。我们的实验从效果上来看,往往都是 transH>transD>transR。为什么效果会有区别?这是因为参数数量不同。transH的参数只有一个法向量wr,transR的参数是一个变换矩阵Mr,transD是对transR约化,参数简化为三个向量wr、wh、wt。从参数数量角度transH
02:基于图传播的模型
图嵌入(graph embedding)就是用一个低维、稠密的向量去表示图中的节点,该向量表示能反映图中的结构信息。两个节点其共享的邻近节点越多,两个对应向量距离就越近。优点就是向量表示可以输入到任何的机器学习模型去解决具体面对的问题。
- Why–从欧式结构到非欧结构
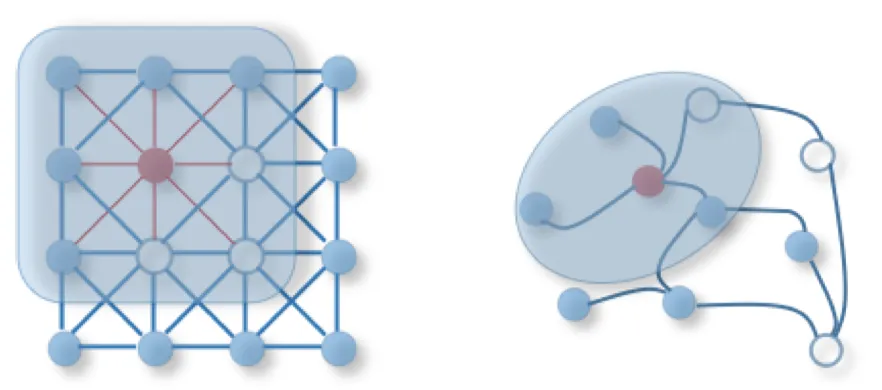
在图像和视频领域利用CNN算法已经取得了巨大成功,但CNN要求数据集必须是欧式结构(下图左),图像和视频数据中的像素点是排列整齐的矩阵正好满足了这一点。如果换到图谱场景,CNN就无能为力了,这是因为图谱是非欧结构(下图右),CNN在非欧结构的数据上无法保持平移不变性,通俗理解就是在拓扑图中不同顶点的相邻顶点数目不尽相同,那么就无法用一个同样尺寸和结构的卷积核在图上通过平移来进行卷积运算。因此需要一套基于图的深度学习模型。
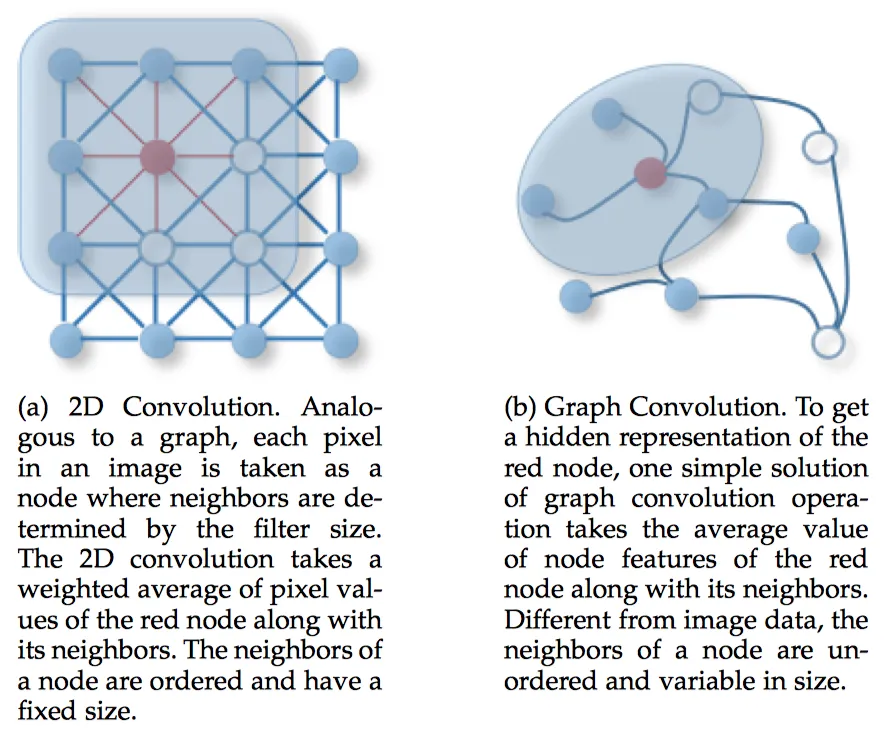
- How–两种求解途径
图谱算法有两种求解途径,在空间域求解(spatial method)、在频谱域求解(spectral method)。
在空间域求解的算法包括:Structure2vec、GNN、GatedGNN、GraphSAGE、GAT、GeniePath等。
在频谱域求解的算法包括:初代GCN、ChebNet等。
本节先从随机游走的算法node2vec开始介绍,然后介绍metapath2vec, COSNET,然后介绍阿尔卑斯平台已经实现的三种有监督算法,它们是Structure2Vec、GeniePath、GAT,最后介绍我们图谱团队自研的算法NCLF和KARI。
node2vec
- 算法介绍
node2vec[23]类似于deepwalk算法,通过随机游走,将图的结构信息表征在节点的嵌入向量中。node2vec主要的创新点在于改进了随机游走的策略(deepwalk完全是随机游走得到两个序列),定义了两个参数p和q,在BFS(广度优先)和DFS(深度优先)中达到一个平衡,同时考虑到局部和宏观的信息,并且具有很高的适应性。
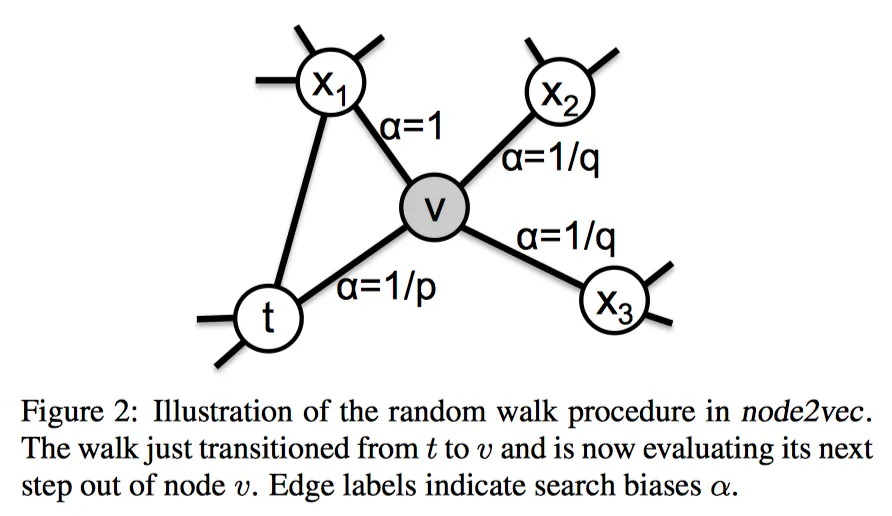
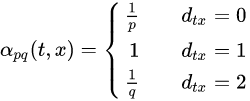
- 流程
第一步,随机游走:从每个节点出发随机游走r次,于是每个节点得到一个path。把这个path当做一个句子,就可以使用word2vec训练了。
第二步,word2vec:将每个词语的one hot向量乘以VxN的矩阵以后向量得到压缩,然后在窗口C范围内计算上下文存在的情况下的条件概率(CBOW),然后通过目标函数训练得到嵌入向量。
优化目标
Node2vec和word2vec是同一套优化目标(loss)。如下图所示,loss定义为遍历所有的v点到u点的概率之和最大化。因为第二个方程的分母上那一项需要对所有节点的两两乘积求和,计算量太大,所以采用了随机采样来近似原来的分布。正样本使用前面随机游走的集合就行,负样本就需要通过随机负采样得到。显然,负采样越多越接近原始的分布。


- 实验
可以看到在无监督模型中,node2vec在随机游走中加入了带有BFS或DFS倾向性的策略以后,比不带倾向性的Deepwalk算法有了明显的提升。
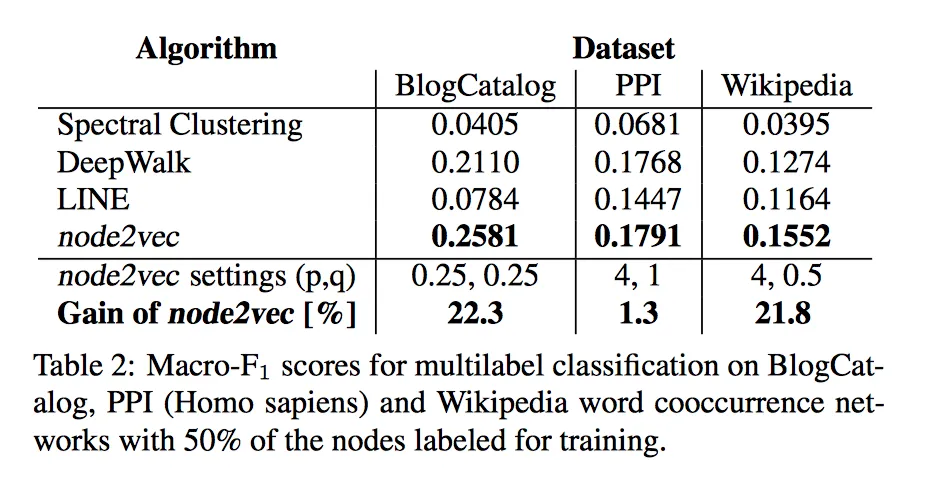
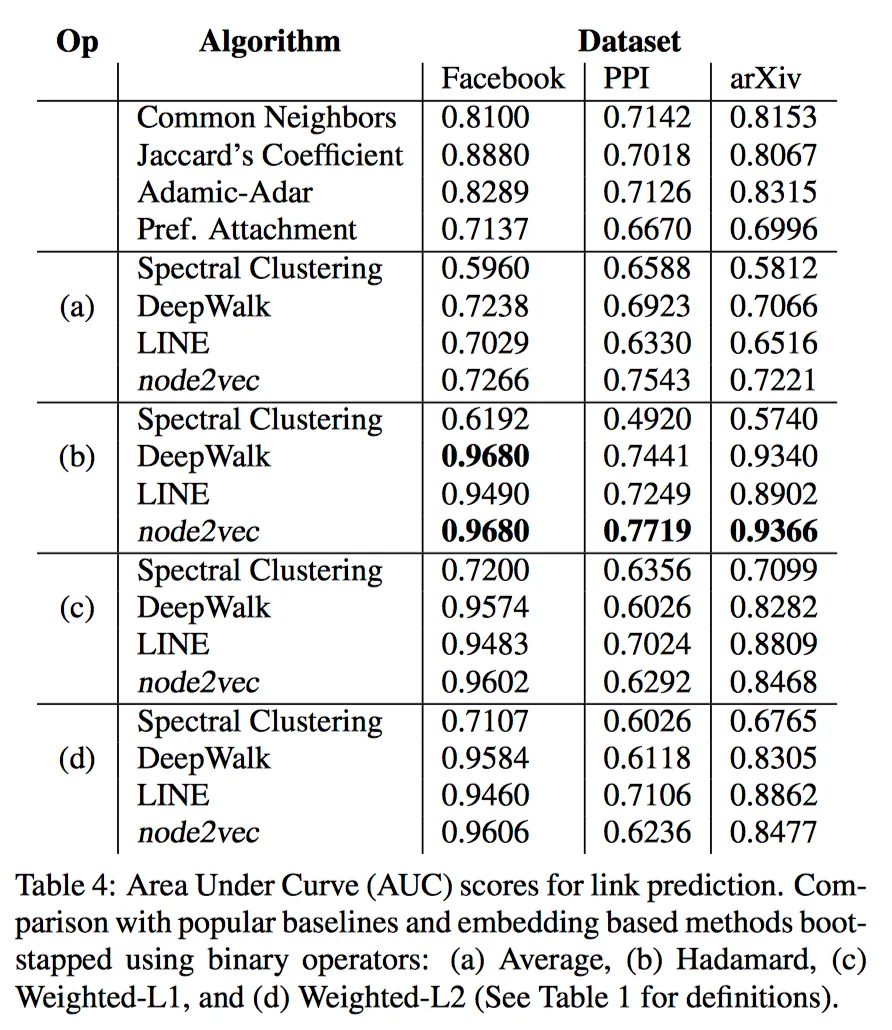
- 应用场景
用于计算节点相似度,可以用于链接预测。因为是无监督学习,不需要打标数据,因此适用范围广。
metapath2vec
- 算法介绍
metapath2vec[24]是2017年发表的,使用基于meta-path的随机游走重构节点的异质邻居,并用异质的skip-gram模型求解节点的网络表示。DeepWalk 、node2vec是同质网络中的表示学习方法,并不能直接应用到异质网络。metapath2vec可以直接在异质图上随机游走,metapath2vec支持多种节点类型以及多种关系类型的异质图,然后学习得到节点的嵌入向量。该论文提出了两种模型,metapath2vec 和 metapath2vec++。
(1)metapath2vec :基于meta-path 机制进行随机游走构建节点序列
(2)metapath2vec++:skipgram 模型中负采样上的改进,把同质网络里的针对所有(类型)的节点随机采样改成了仅对当前节点类型的节点进行采样。
metapath:元路径是一种通过一组关系连接多个节点类型的路径,可以用来描述异质网络中不同类型对象之间各种连接不同语义关系。
该论文形式化了异构网络表示学习问题,目标是同时学习出多种节点的低维度隐式的嵌入向量,metapath2vec的目标是最大化保留给定异构网络的结构和语义的可能性。
其中随机游走的转移概率,需要遵从给定的metapath,比如说按照metapath下一个节点类型是t, 那么邻居节点中是t类型的节点才有可能被选择,其他类型的节点或者非当前节点的邻居节点一概不会被选择到。
- 算法步骤
第一步是按照metapath的规则随机游走,获取path。
(1)给定metaPath 后算法按照 metaPath 去游走,直到路径长度达到Walk Length。
(2)给定的metaPath必须首尾两个结点的Type一样,正确的格式例子: “ABCA”,“VDEEV”,“ABA”等。
(3)如果给定metaPath为“ABDSA”,walkLength为10,则游走得到的结果将是 “ABDSABDSAB”,达到10个结点是会截断。
第二步将metapath游走获取的path作为“句子”,交给word2vec,采用skip-gram学习出嵌入向量。
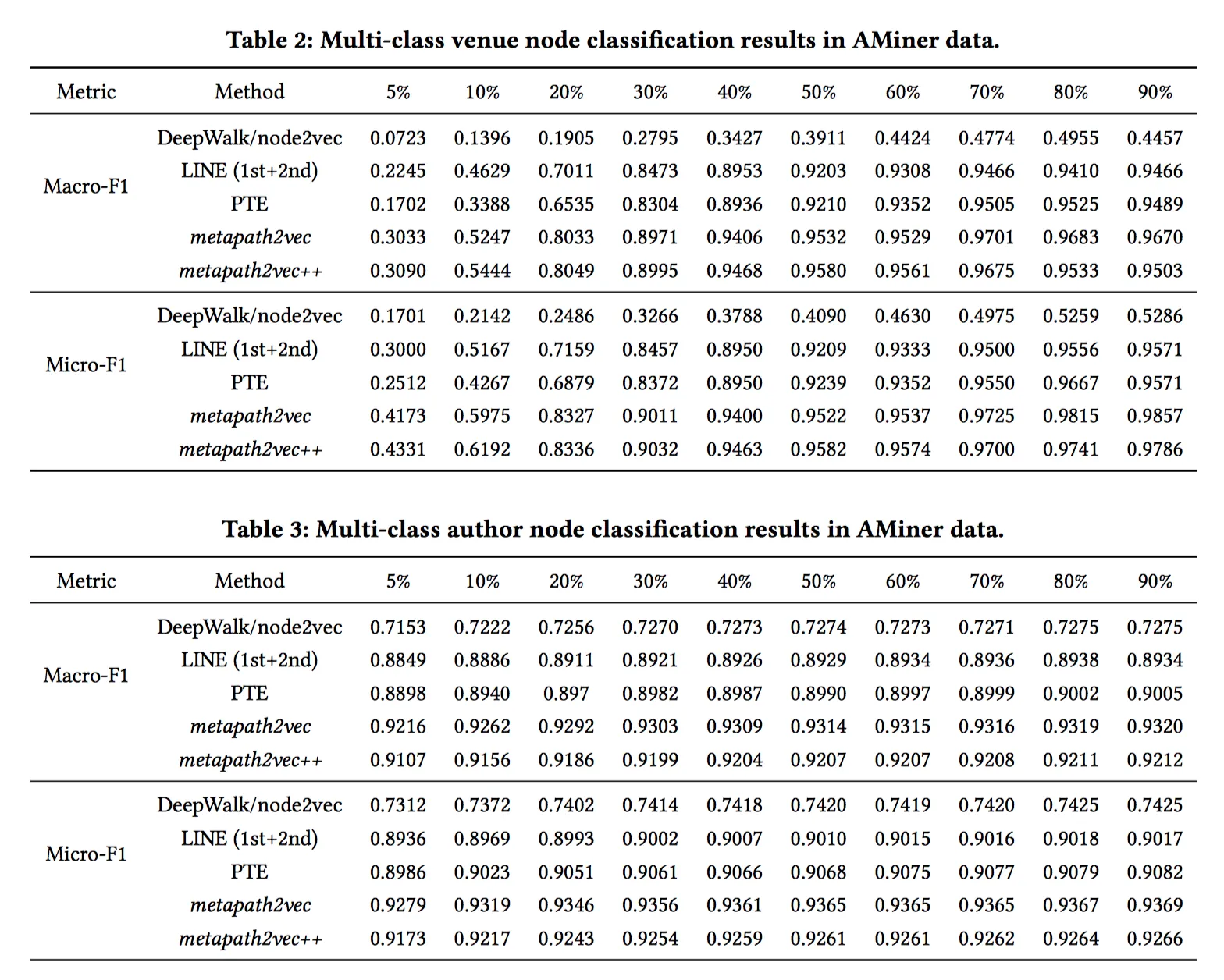
- 实验
文章做了节点分类,节点多分类,节点聚类,可视化,参数敏感性分析等实验。metapath2vec 相比较于其他方法(多是典型的同构图上的方法),结果还是具有非常明显的提升的。只不过metapath2vec++ 在节点多分类上的表现还是明显弱与metapath2vec的。
COSNET
- 算法介绍
COSNET[25]是2015年发表的,初衷是将不同的社交网络集成在一起,比如Twitter、Myspace、LiveJournal、Flickr、Last.fm。这些不同的社交网络是异质图,边的类型是不同的。COSNET是一个有监督模型,其思想是将全局一致性和局域一致性结合在一起作为目标函数,通过打标数据的学习让模型的预测结果尽量在全局和局域都保持一致。

目标函数来源于三个部分: 项代表全局一致性,
项代表全局一致性, 项代表局域(两跳范围)一致性,
项代表局域(两跳范围)一致性, 项代表局域(三跳范围)一致性。
项代表局域(三跳范围)一致性。

其中 是候选配对,
是候选配对, 是标签表示配对是否正确。
是标签表示配对是否正确。
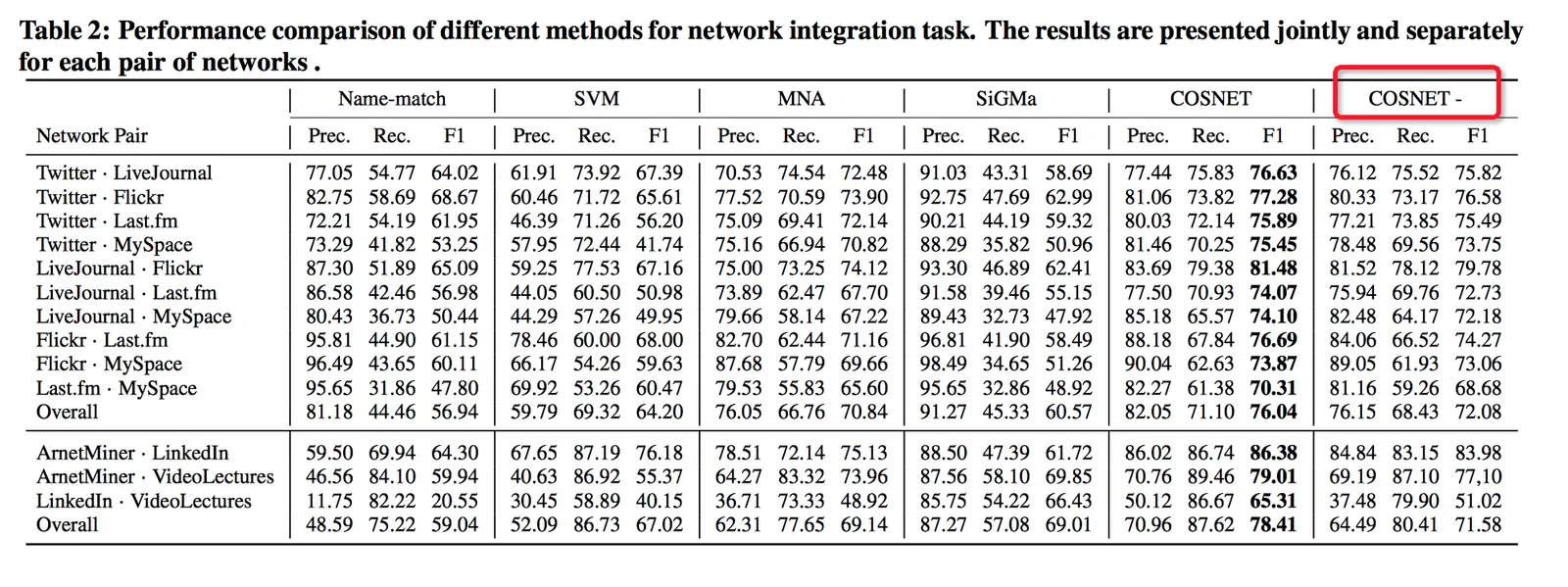
- 实验
该算法的效果比之前的算法效果有一定的提升,但是提升有限。见下表,一方面COSNET比按照最基本的用户名id匹配(图中“name-match”那一列)只提升十多个百分点;另一方面,“COSNET-” 那一列显示减掉全局一致性效果以后只有1个百分点的变化,说明本文重点引入的全局一致性没有起到明显作用。
GCN
- 算法原理
一般来说GCN[26-28]分为两大类,一种是在傅里叶域进行卷积变换;另一种是“空间域卷积”,是直接在图上进行卷积。谱图卷积有一套统一的理论支持,但是有时候会受到图拉普拉斯算子的限制。下面两幅图分别展示了一度和两度的图卷积,其中红色的点就是卷积范围。

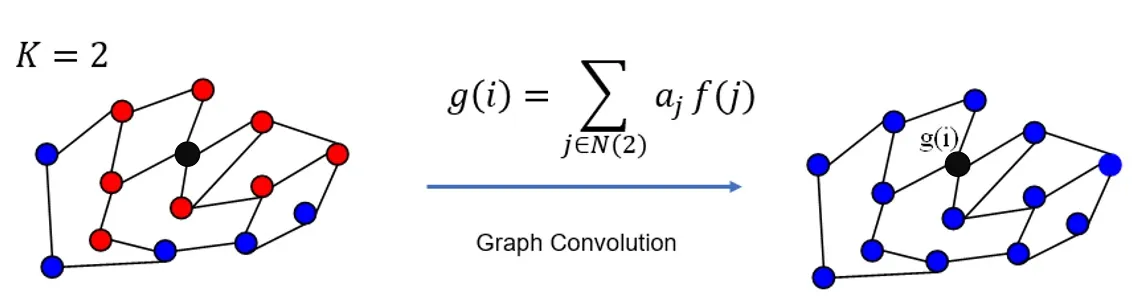
图:一度和两度的Graph Convolution示意图
文献[28]中的方程(3)-(5)很好的描述了如何从空间信息的卷积开始,推导出方便应用落地的卷积核的过程,原文如下:

上面方程(3)是把CNN的卷积从图像搬到了图谱上。可以与CNN进行类比,这里的结构函数g就是核函数,这里所有节点的特征构成的矩阵x就相当于CNN里被卷积的图片。CNN是对图片做卷积,而GCN是对节点特征做卷积,如下图所示。
为了更好的理解GCN,我们再与CNN做更多的类比。第一代的GCN[26]的卷积核的尺寸是整个图谱,如上面方程(3)所示,相当于对图谱做全局的卷积。这样做的计算量太大,因此后续的GCN做了近似,其中最经典的是Kipf那篇工作[28],如上面方程(4)所示采用了切比雪夫多项式,并取前K项作为卷积核的近似,K就对应了选取K跳的邻居范围(实践中往往K取2、3)。这就相当于把一个全局的卷积核更换为一个局域的卷积核。后面可以看到K=2、3时切比雪夫多项式是平方、立方项,这是对原生的GCN做了一个比较粗糙的近似,幸亏我们还可以为每一项加上权重用标签来学习来弥补这一误差。
这里解释一下拉普拉斯算子的含义。原生的拉普拉斯算子等于每个节点的度减去其邻居,即L=D-A,D就是度矩阵,这是一个对角矩阵,A是邻接矩阵。L乘x相当于把每个节点的信息传播给了其邻居节点。这里拉普拉斯算子本质是一个二阶差分,物理上就是将其作用的对象以正比于其梯度的力度传播到附近的点。
注:卷积定理。函数卷积的傅里叶变换是函数傅立叶变换的乘积。可以表达为下面的方程,即对于函数 与
与 两者的卷积是其傅立叶变换
两者的卷积是其傅立叶变换 与
与 的乘积的逆变换:
的乘积的逆变换:

因为方程(3)里面两个本征矩阵U相乘的计算量太大O(N2),因此方程(4)采用了切比雪夫多项式展开来近似。那么方程(3)就被近似为方程(5),多项式的阶数对应了传播几跳范围。切比雪夫多项式如下:

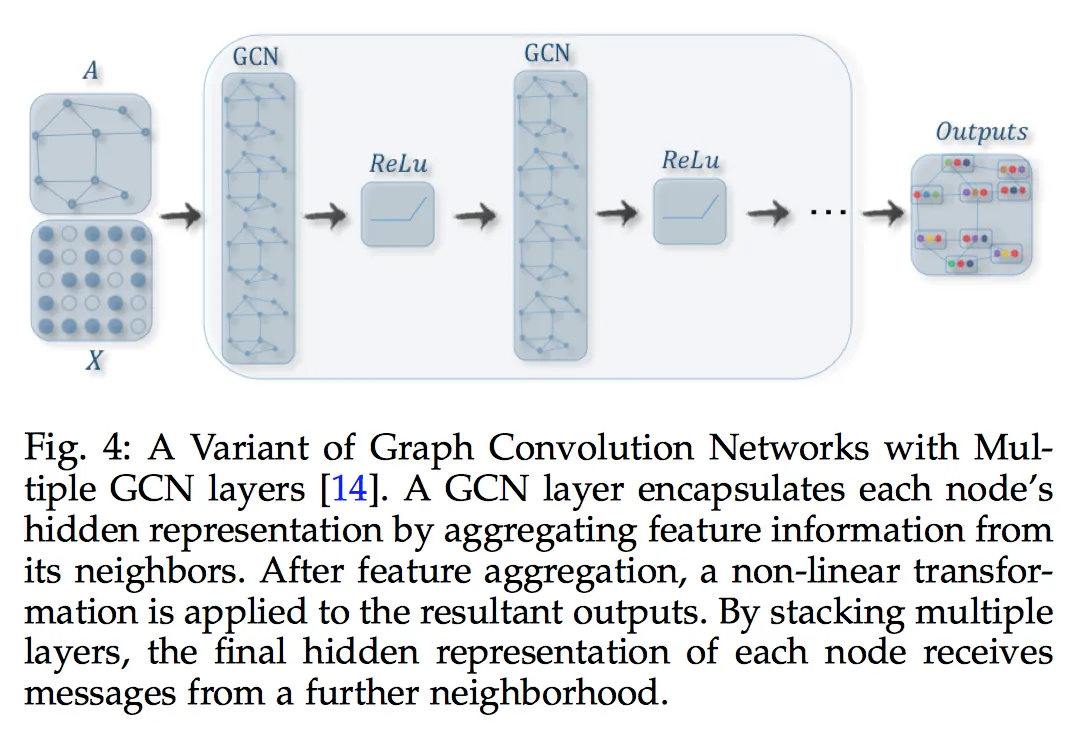
GCN中,一度聚合相当于一层卷积层,K度聚合相当于K层卷积层。同CNN一样,因为所有卷积层(aggregator)具有共享参数这个优点,所以才能通过喂打标数据的方式来学习这些参数。共享参数的方式也极大的降低了参数空间,让模型具有scalable的优点。上图中多层GCN卷积层结合ReLu激活函数,让节点可以接收到更远邻居的信息。
GCN卷积层的具体表达式如下,从t到t+1层的传播可以表示为:

其中 是归一化邻接矩阵,H是节点的表示向量,W是模型参数。
是归一化邻接矩阵,H是节点的表示向量,W是模型参数。 ,
,  .
.
- 应用场景
适用的场景包括:节点属性预测(属性分类/回归)等,但有限制,只适用于双向图。
trick:当数据分布不均匀时(即绝大部分边集中于少数节点之间),一个技巧就是,在采样取K度邻居的过程中,采取限制最大邻居数量等类似手段,可以对节点(特别是头部节点)采样的邻居数量进行限制。
- 实验
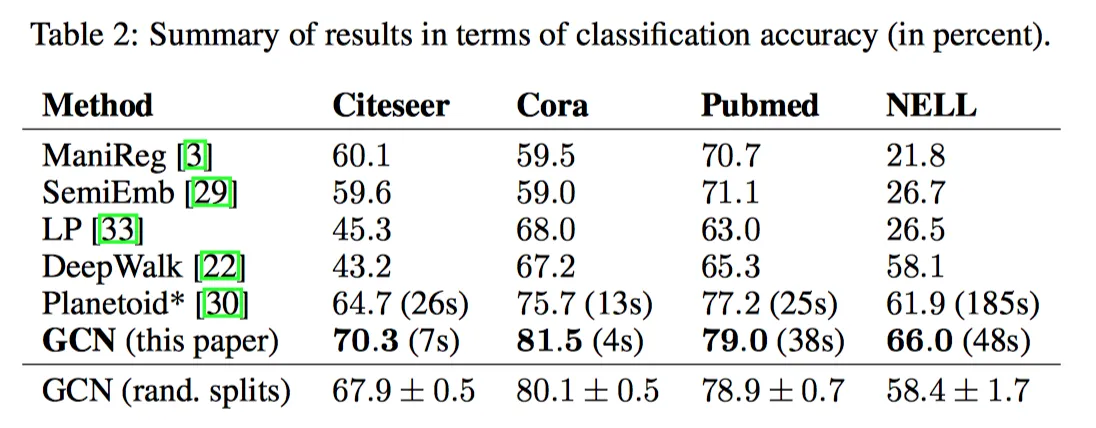
可以看到GNN的实验效果明显好于基于随机游走的Deepwalk等基础算法。
Structure2Vec
- 算法发展脉络
kernel methods在2002年代是处理结构化数据的代表方法,包括两类:基于bag of structures和基于probabilistic graphical models (GM)。但是kernel methods特别依赖于核函数(即特征空间)的设计。缺点是不能处理大规模图。
为了能够处理大规模图,宋乐老师团队开发了Structure2Vec[29,30]。因为不需要存储核矩阵(kernal Matrix)所以占用内存小了很多,应用了随机梯度下降后也具有处理大规模图的能力。Structure2Vec包含了两种传播方式Mean Field 和 Loopy Belief Propagation(后来扩展到了更多种传播方式)。
- 算法原理
Structure2Vec[29,30]是什么:
是一个基于知识图谱的深度学习和推理算法,是一种graph embedding算法。不仅仅考虑节点的特征,还考虑了节点和边之间的相互作用以及传播。
-
- 聚合算子
讲解原理之前首先介绍聚合算子的概念。图谱可以看作由多个中心节点和对应的邻居节点组成。下一步需要考虑的就是如何将信息从邻居节点汇聚到各个中心节点。下图给出了2跳聚合算子的示例,中心节点A的表示是由其邻居节点B、C、D的信息聚合而来,而节点B、C、D的信息是由它们各自的邻居信息聚合而来。最终得到了聚合算子(aggregator),其作用是对邻居节点的信息进行聚合。为了方便理解,我们类比CNN,聚合算子就相当于卷积层,因为他们都起到了将周围点的信息汇聚起来的作用。
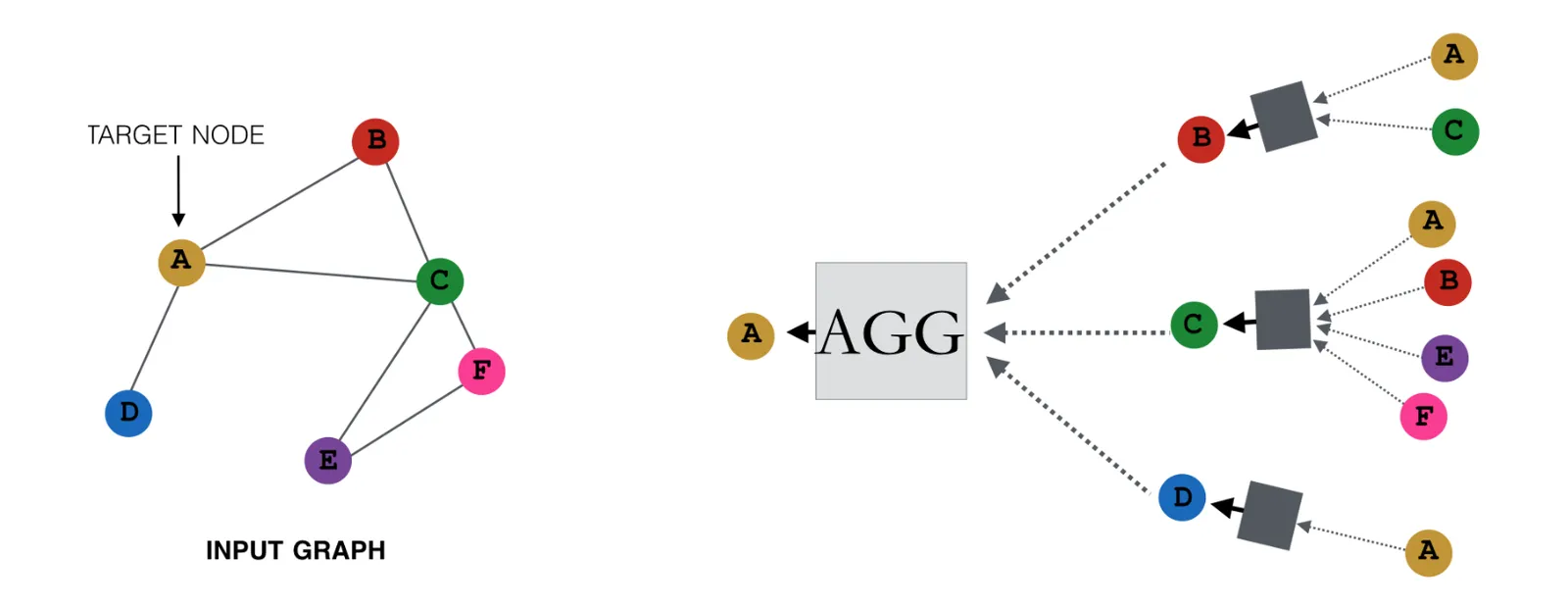
图: 两跳聚合算子示例
-
- 解决痛点:
解决了以前的深度学习技术难以用于诸如图形、网络和动态网络等组合结构数据的表示和特征学习。
-
- 基本原理:
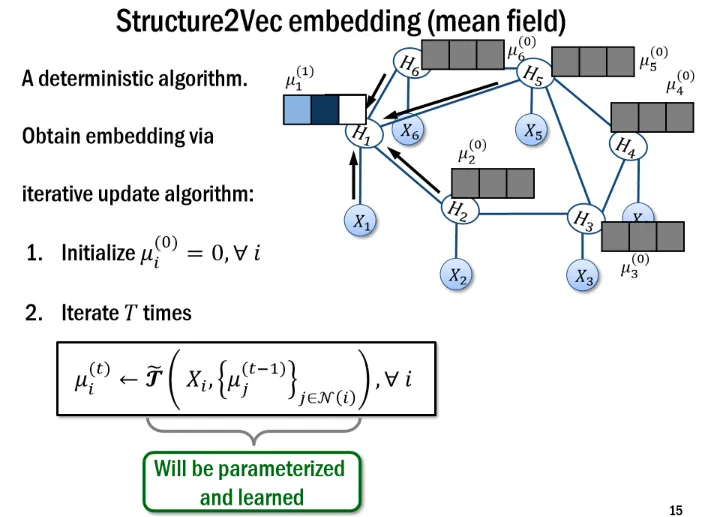
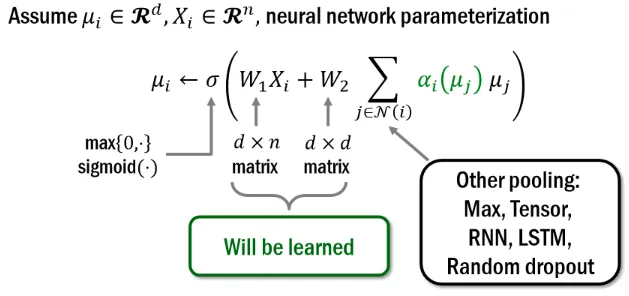
图: Structure2Vec的基本原理[30]
-
- 变量解释
Yi:节点i的标签(label)
Xi: 节点i的属性值(value of attribute)
Hi: 是一个隐变量,是输入Xi的代言
 :节点i的向量化表示,其初始化是通过对特征进行信息抽取得到。
:节点i的向量化表示,其初始化是通过对特征进行信息抽取得到。
W1、W2:节点i与自身以及与邻节点的相互作用,包含了图结构以及节点的特征信息。
V:节点i的特征向量 与输出Yi‘之间的转换矩阵。注意参数W2和V并不是针对某一个节点的,而是整个网络都采用这同一套参数,即共享参数。
与输出Yi‘之间的转换矩阵。注意参数W2和V并不是针对某一个节点的,而是整个网络都采用这同一套参数,即共享参数。
n:节点特征维度。
d:特征向量 的维度。
的维度。
-
- 算法流程
(1)对于第i个节点,该节点的特征信息传递给自己,邻居的信息再传递过来。然后经过K度传播,可以获得以i节点为中心的一个subgraph,作为训练集的一个基本单位。
(2)最小化损失函数 loss=(Yi-V )2。采用训练集训练(随机梯度下降),通过最小化损失函数得到模型W1,W2,V。
)2。采用训练集训练(随机梯度下降),通过最小化损失函数得到模型W1,W2,V。
(3)在infer过程中,先获取节点i的K度subgraph,然后将该subgraph带入模型便可以得到该节点的嵌入向量以及预测结果。
说明:这里介绍的是Mean Field方法,另外作者在文章中还介绍了一种方法Loopy Belief Propagation。这两种方法的区别是:前者的信息传播过程是,在一个超步内,通过对每一个相关节点上的信息进行收集得到的。后者的信息传播过程包含两步,在一个超步内,第一步对每条边上传播的信息进行汇总,第二步再对每条经过节点i的边上面的汇总后的信息进行收集。
-
- 算法能力
Structure2Vec提供了一种能够同时整合节点特征、边特征、网络结构以及网络动态演化特征的深度学习和推理嵌入技术。它可以对网络中的节点和边进行推理,能够挖掘出节点之间的二度、三度甚至更深层次的关系。Structure2Vec平台支持十亿节点、百亿边规模的图模型训练,并且对于实际小于百万节点的小规模业务场景,其也支持使用单机模式迅速训练,用户可以根据自己的需要进行随意切换或让系统自动切换。Structure2Vec平台提供了一整套流式解决方案,从用户原始数据检查、到模型训练和导出模型和预测结果给业务,都可以通过简单配置设置例行运行。
-
- 加速机制
1). 矩阵乘法采用GPU加速;
2). T度传播,当T较小的时候,可以只加载局部图;
3). 利用Parameter Server进行分布式计算。
- 应用场景
Structure2Vec需要与有监督学习相结合。其应用分为两类,一类是应用于静态图,一类是应用于动态图。
静态图应用中,Structure2Vec可以分别对节点、边、子图的结构进行分类或回归。应用举例:
1) 垃圾账号识别,这属于节点分类问题。账号和设备之间的登录情况构成图谱,并且账号和设备也各自具有特征。然后利用带有标签的账号数据对经过T次信息传播后的模型进行训练,得到传播权重W1、W2和分类参数V以及每个节点(账号)的嵌入向量 。有了这些参数和嵌入向量就能对未打标签的节点进行预测了。
2) 基于分子结构预测光伏作用大小的问题,如下图所示,这就属于子图结构预测问题(预测的是连续值所以这是回归问题)。首先经过T次传播,然后通过训练得到了传播权重W1、W2和分类参数V以及每个节点的嵌入向量。训练的目标函数是通过对这些嵌入向量的加权求和来表示光伏作用的大小,然后与打标的target之间的平方差定义为loss。训练好了模型以后,就可以预测新的分子结构的光伏作用大小了。
3) 通过药物分子结构预测药物效果,就属于利用结构信息进行分类的问题,原理和过程与2)类似只是由回归问题变成了分类问题。
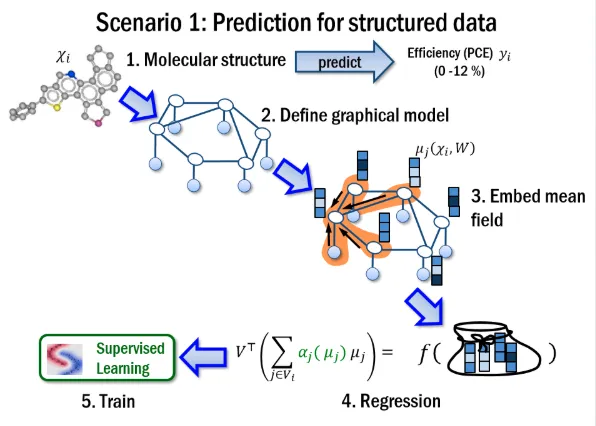
图:利用Structure2Vec基于分子结构预测光伏作用大小的问题
- 实验
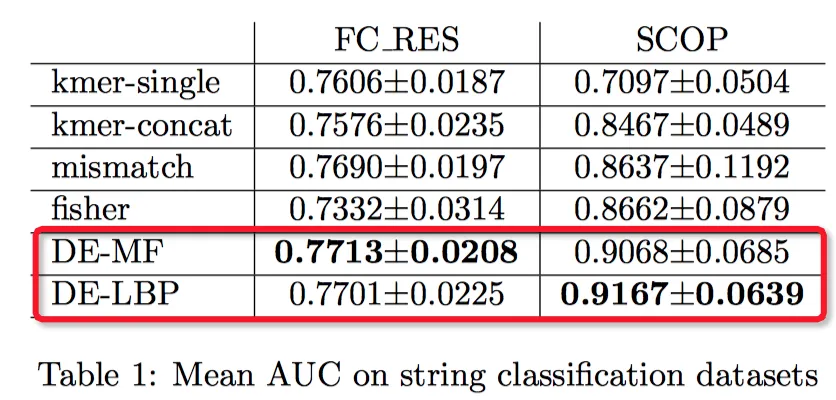
FC_RES数据集描述的是RNA将基因片段定向到DNA。SCOP数据集是蛋白质结构分类,这两个都是子图分类问题。前面四种算法都是kernal method,后面两种是Structure2vec的两种实现方式。可以看到Structure2vec的效果明显好于kernal method。
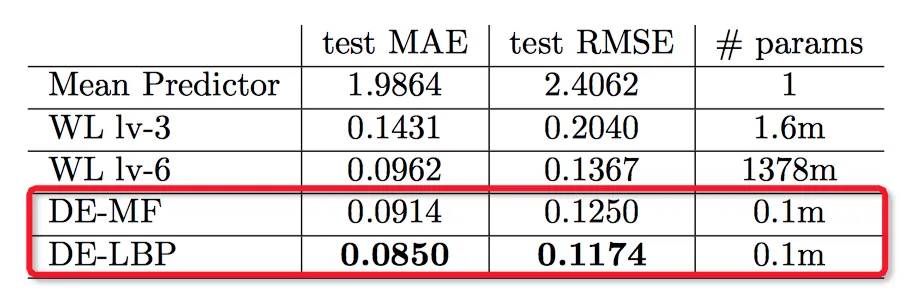
这个实验是基于分子结构预测光伏作用大小的问题,WL是kernal method,后面两种是Structure2vec的两种实现方式。MAE是平均误差,RMSE是均方根误差。可以看到Structure2vec的效果明显好于kernal method。另外,一个重要的区别是kernal method是not scalable的,而Structure2vec是scalable的,实验中WL lv-6对于百万大小的数据集其参数数量比后两者多了1万倍,速度却只慢了两倍。
动态图应用中,多了一个时间轴,Structure2Vec可以对节点之间是否会发生交互以及交互的概率进行预测。应用举例:
1). 推荐系统。User和iterm随着时间的交互展开成一个单一方向的图结构,如图所示,通过强化学习得到嵌入向量,对某个时刻的user和item的嵌入向量做内积,就能判断二者在该时刻的交互发生的概率。
2). 对事件的预测,与1)同理。
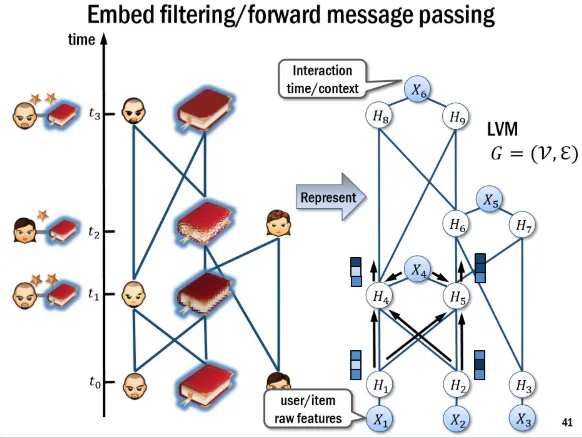
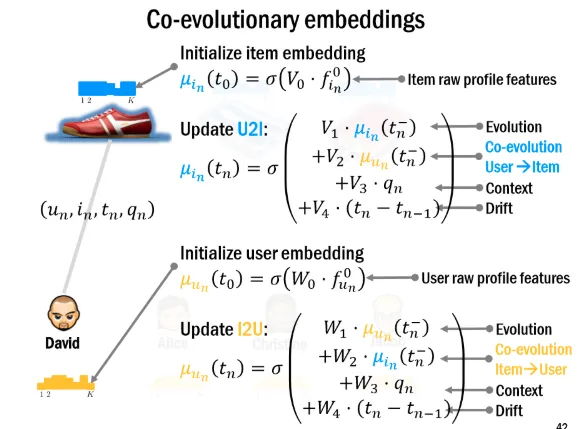
图: 利用Structure2Vec基于时间动态演化进行商品推荐
应用情况:目前Structure2Vec在信用评估、推荐系统、行为预估、垃圾账号识别、保险反欺诈以及芝麻信用团队的反套现模型中都取得了非常好的效果。
GraphSAGE
- 背景介绍
GraphSAGE[31]和Structure2vec比较类似,都是由聚合算子构建起来的图计算模型,都是共享参数的模型。GraphSAGE是比较早期的经典GNN算法,来自斯坦福发表于2017年。很多文献都会和GraphSAGE进行比较。这篇文章明确提出了图算法中的transductive learning和inductive learning的区别。
直推式(transductive)学习:从特殊到特殊,仅考虑当前数据。在图中学习目标是学习目标是直接生成当前节点的embedding,例如DeepWalk、LINE,把每个节点embedding作为参数进行学习,就不能对新节点进行infer。
归纳(inductive)学习:也就是平时所说的一般的机器学习任务,以共享参数方式进行学习。从特殊到一般:目标是在未知数据上也有区分性。
- 算法原理
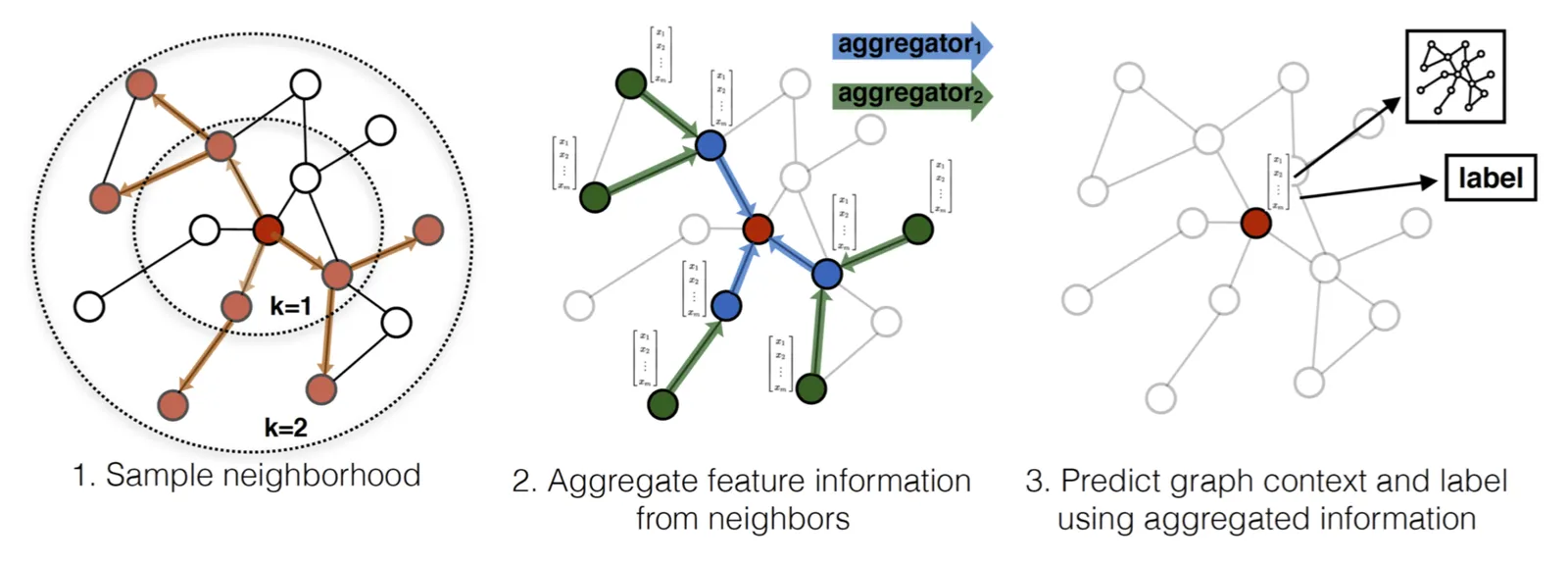
GraphSAGE同样采用聚合算子,其信息聚合的过程如上图所示,可以描述为以下三个步骤:
-
- 先对邻居随机采样,降低计算复杂度(图中一跳邻居采样数为3,二跳邻居采样数为5)
- 生成目标节点嵌入向量:先聚合2跳邻居特征,生成一跳邻居嵌入向量,再聚合一跳邻居嵌入向量,生成目标节点嵌入向量,从而获得二跳邻居信息。
- 将嵌入向量作为全连接层的输入,预测目标节点的标签。
算法伪代码如下:

其中4、5行的for循环描述了汇聚算子的工作过程。第4行描述了信息由k-1层汇聚到第k层。第5行描述了中心节点信息由中心节点的k-1层信息与中心节点的邻居信息进行拼接,并通过一个全连接层转换,最终得到中心节点在第k层的嵌入向量。
GraphSAGE提出了四种不同的聚合方式:平均聚合、GCN归纳聚合、LSTM聚合、pooling聚合。
a. 平均聚合:先对邻居embedding中每个维度取平均,然后与目标节点embedding拼接后进行非线性转换。
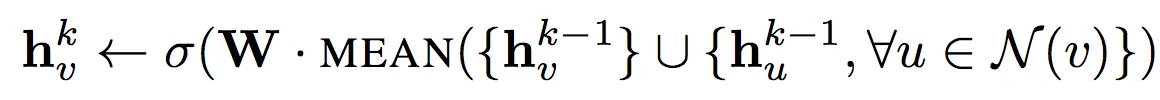
b. GCN归纳聚合:直接对目标节点和所有邻居e服务器托管网mebdding中每个维度取平均(替换伪代码中第5、6行),后再非线性转换:
c. LSTM函数不符合“排序不变量”的性质,需要先对邻居随机排序,然后将随机的邻居序列嵌入向量作为LSTM输入。
d. 先对每个邻居节点上一层嵌入向量进行非线性转换(等价单个全连接层,每一维度代表在某方面的表示),再按维度应用 max或者mean pooling,捕获邻居集上在某方面的突出的或者综合的表现 以此表示目标节点嵌入向量。
- 实验结果
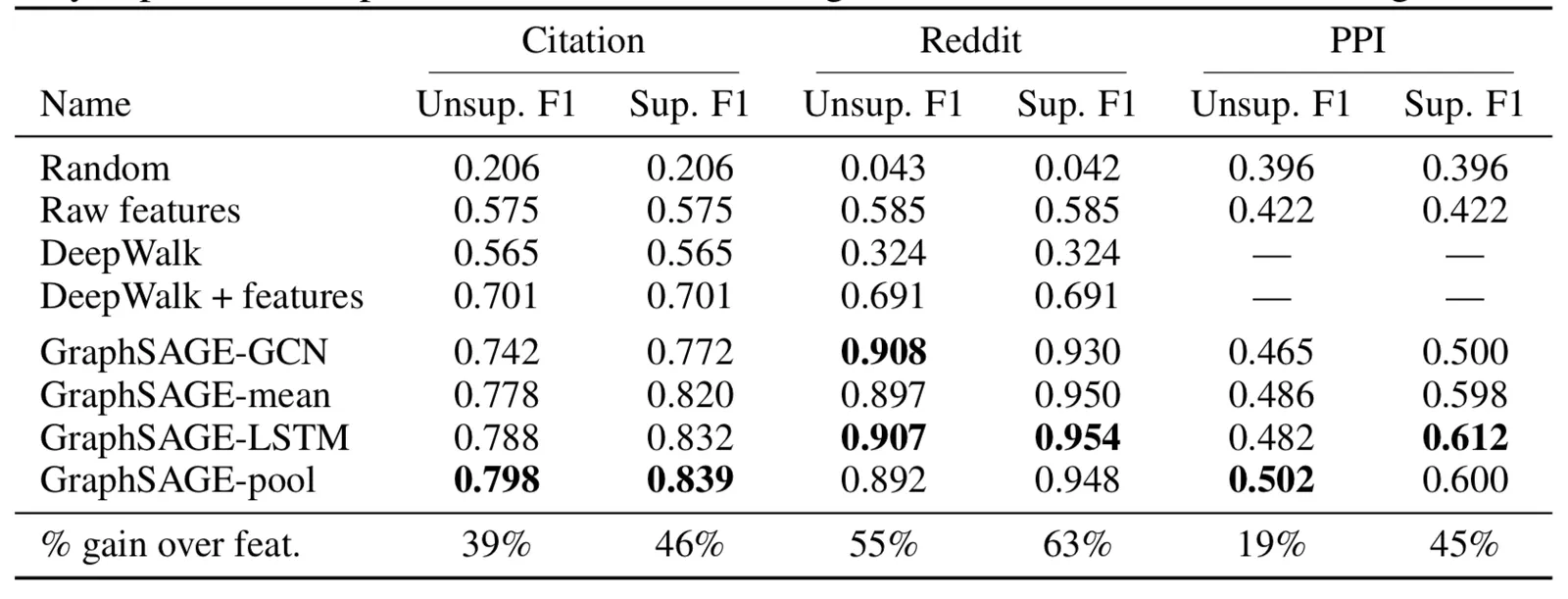
从实验结果上可以看到GraphSAGE的四种聚合方式比传统算法均有所提升。
GAT
- 算法描述
Graph Attention Networks (GAT)[32]算法的主要思想是利用attention机制来代替GCN中的卷积层,得到node embedding。同时该算法可以适用于transductive和inductive两种任务。transductive任务是指测试集的节点和节点特征在训练过程中出现过;inductive任务是指测试集中的节点不会在训练过程中出现。下面介绍其核心结构Graph Attention layer.
- 基本原理
对于每一层,输入为每一个节点的feature, h={h1,h2,⋯,hN}, hi∈RF,N为节点个数,F为输入特征维数。输出亦为每一个节点的feature, h’={h′1,h′2,⋯,h′N}, h′i∈RF′,F′为输出特征的维数。则attention 机制就是在对输入特征做线性变换W∈RF′F后计算对于节点i其周围节点(包括自身)的权重,最后加权求和通过激活函数即得到节点i的输出特征。则节点j对节点i的权重(可以看做节点j对于节点i的重要性)为:

其中 就是attention机制,后面会给出几种具体的形式。则节点i输出可由对其相邻点加权得到:
就是attention机制,后面会给出几种具体的形式。则节点i输出可由对其相邻点加权得到:

上面这一步softmax为对权重的正则化。

上面这一步就是一个加权求和。注意到这个模型只用到了节点特征,没有用到边的信息。
文中给出的attention 机制有两类:一类是单层网络,如下:

另外一类是多头注意力网络(multi-head attention)的两个例子,第一个例子是将不同的head得到的嵌入向量做拼接,第二个例子是做平均,如下:


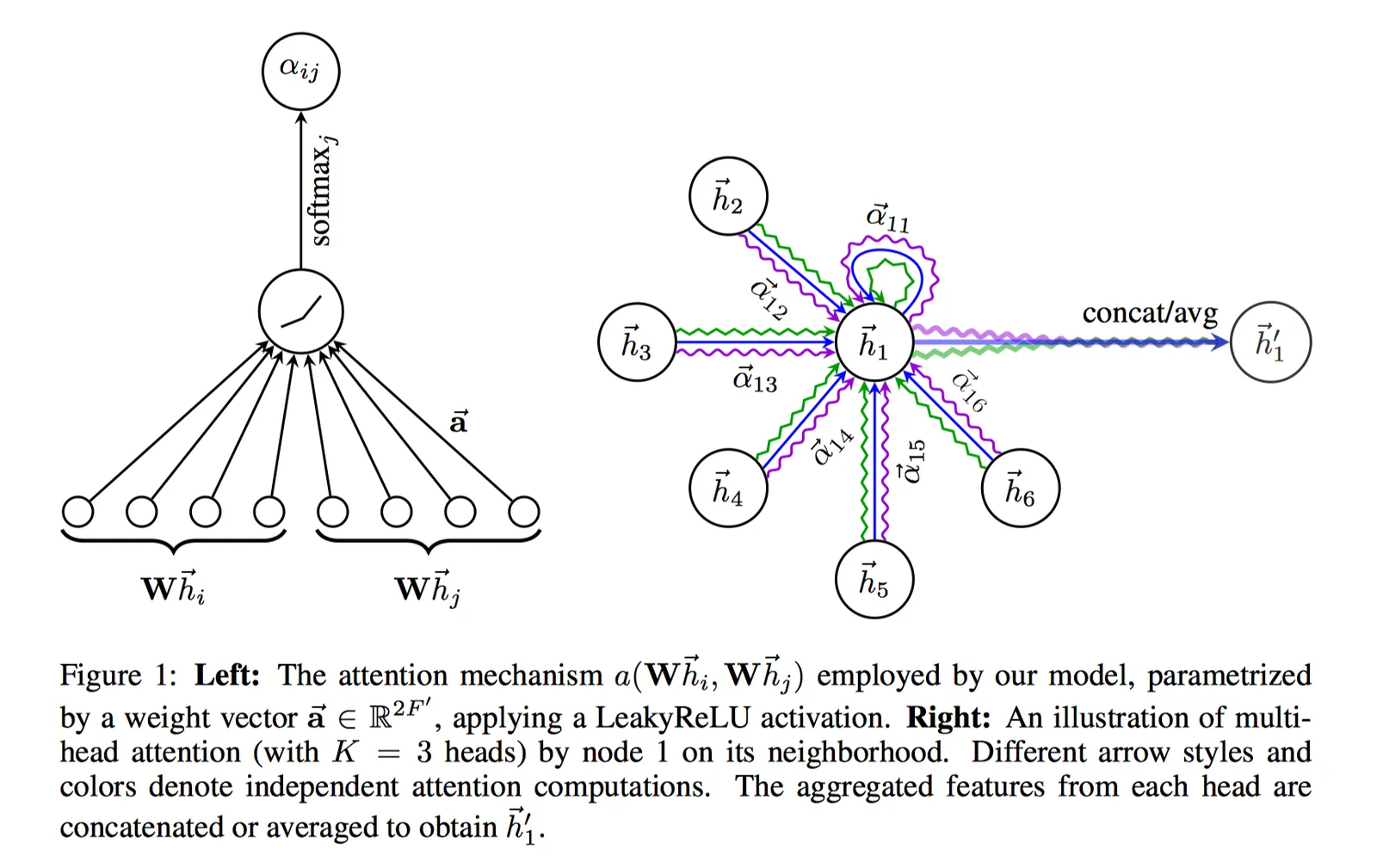
图: Graph Attention Networks (GAT)算法的Graph Attention layer图示
因为Attention计算相互独立,方便并行计算,所以比传统的GCN高效。
- 实验结果
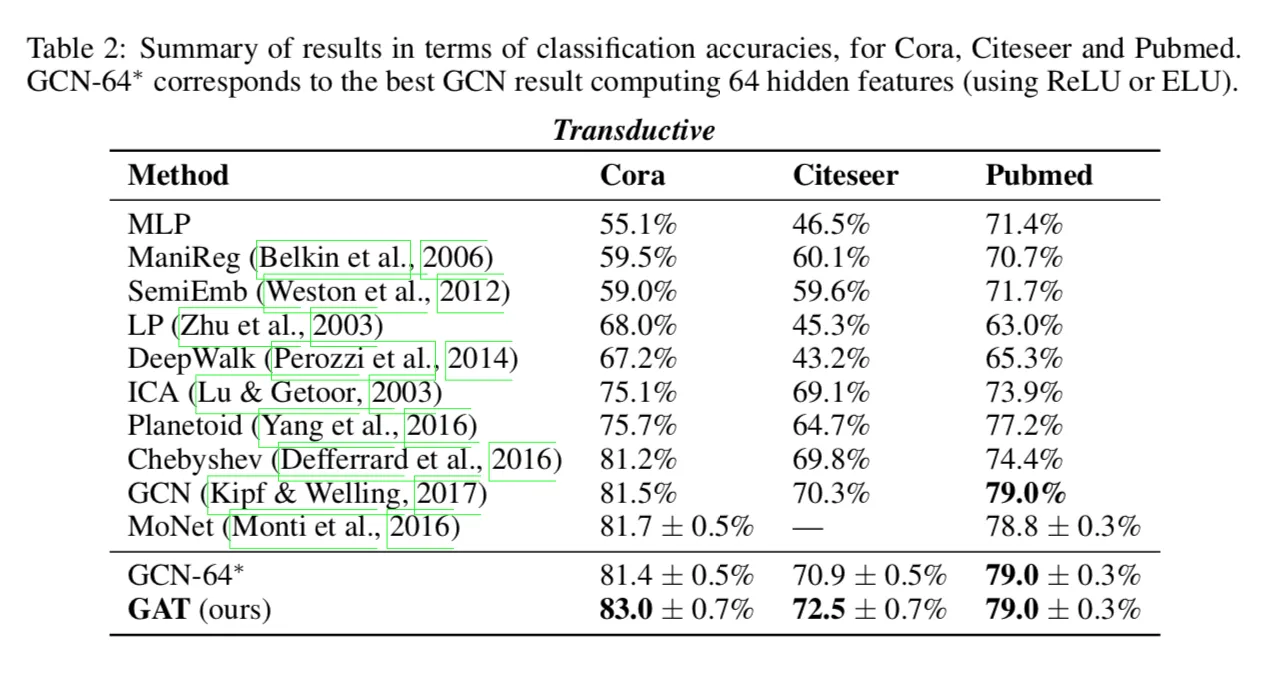
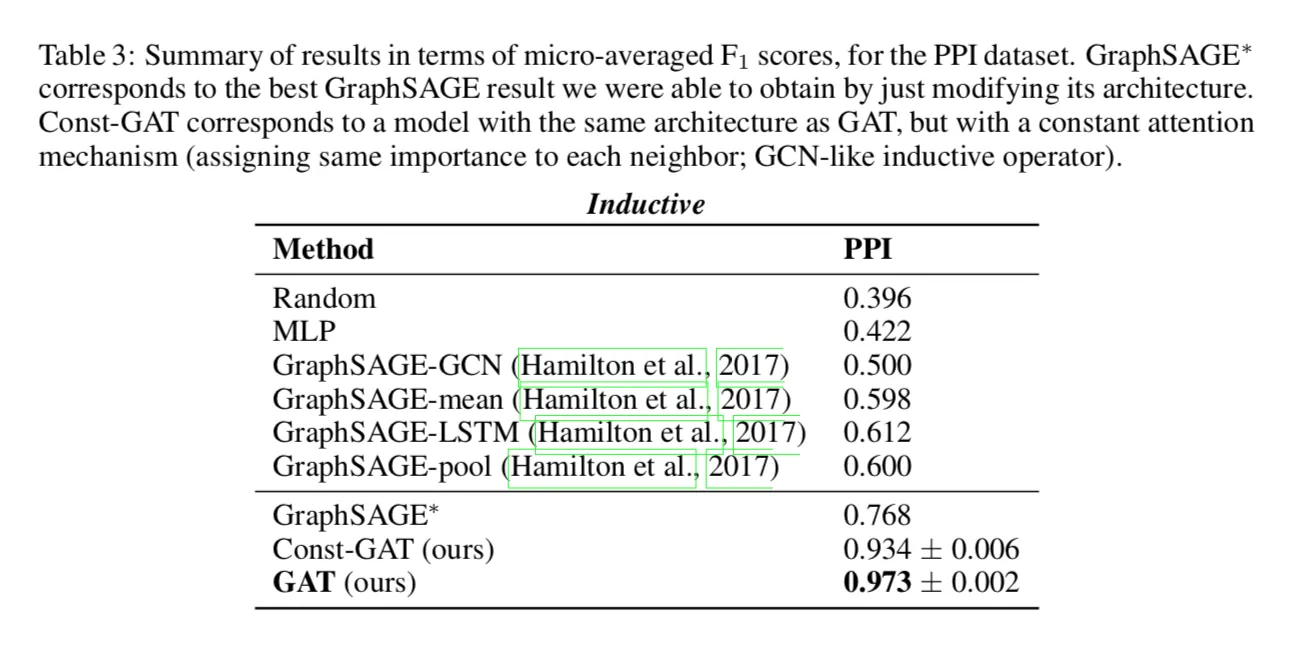
可以看到实验结果都还不错,尤其是PPI的结果,比GCN的结果高太多了。文章发表在ICLR 2017[32]上。
- 算法特点:
GAT算法和下面将要介绍的GeniePath算法比较相似,都是建立在GNN基础之上,只是GAT只添加了对邻居节点信息进行筛选的attention机制,而GeniePath除此之外,还采用了LSTM机制来过滤经过多层传播的信息。从效果来讲,这两种算法的表现也比较接近,并且二者的表现都明显好于之前的GNN算法。
- 应用场景:
因为算法特性一致,GNN能够使用的场景(比如前面Structure2Vec的应用场景),GAT理论上应该都适用。
GeniePath
- 算法发展脉络:
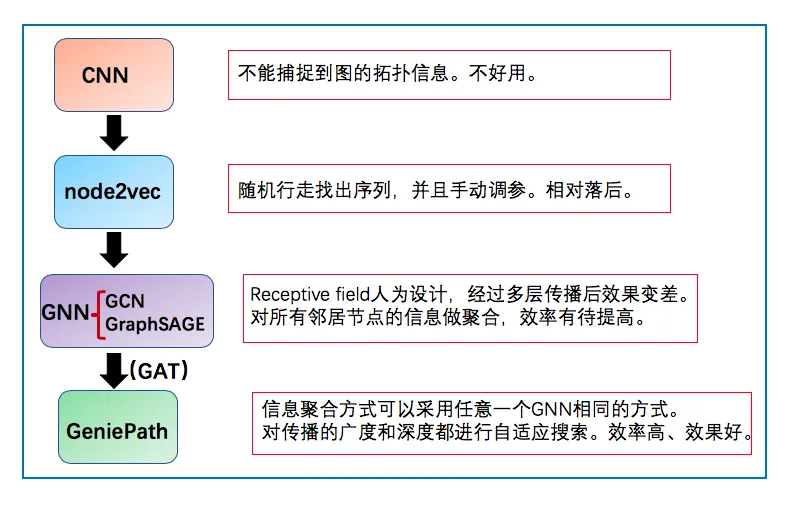
图: GeniePath算法的发展脉络
GraphML团队开发的GeniePath算法[33,34]可以在聚合算子上结合节点的属性信息来判断到底有多少信息需要传播,有多少信息可以过滤掉。简单来讲就是,和structure2vec相比,GeniePath的聚合算子不仅仅采用了结构信息而且还结合了节点属性信息,就具有了更强大的表达能力。
- 算法原理:
下图揭示了GeniePath的算法结构,其结构是在基本的聚合算子上做了扩展。虚线左边表示在广度上采用了attention机制来筛选邻居节点;虚线右边表示在深度上采用了LSTM机制来过滤经过多层传播的信息。
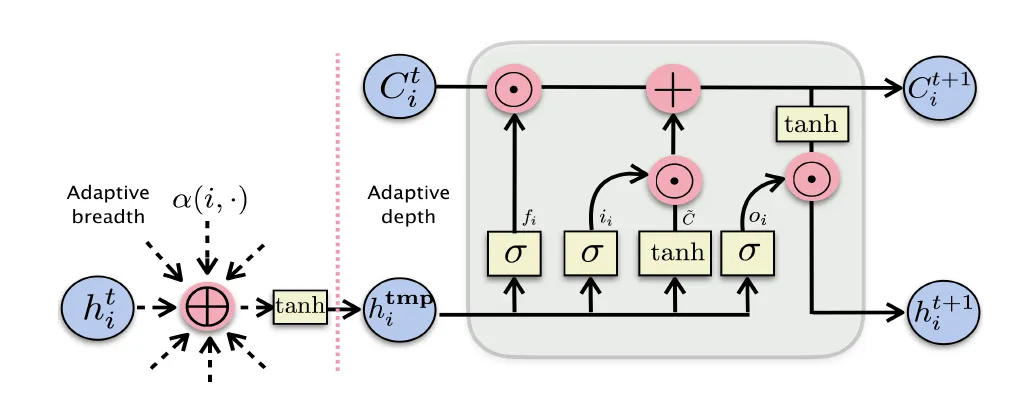
下面的方程就描述了GeniePath在深度上的attention机制以及广度上的LSTM机制。
-
- LSTM机制:

其中 是输入门;
是输入门; 是遗忘门;
是遗忘门; 是输出门。
是输出门。
-
- Attention机制:
 (8)
(8)
GeniePath沿用GNN的计算框架,其特点在于会根据优化目标自动选择有用的邻居信息,来生成节点特征(embedding)。GeniePath通过定义两个parametric函数:自适应广度函数、和自适应深度函数,共同对子图进行广度、深度搜索。其中自适应广度函数限定朝哪个方向搜索重要节点,自适应深度函数限定搜索的深度。实现中如上图所示,GeniePath使用一个attention网络表达自适应广度函数来来筛选邻居节点,使用一个LSTM-style网络表达自适应深度函数来过滤经过多层传播的信息。GeniePath后来进行了升级,不仅能考虑节点特征,还能考虑边的特征。
目前所有的图神经网络方法都基于如下框架,做T次迭代,相当于每个节点拿自己走T跳可达的“邻居”节点,来做传播和变换,最后的被用来直接参与到损失函数的计算,并通过反向传播优化参数。在GeniePath之前的算法:Structure2Vec、GCN、GraphSAGE,他们的共同特点是对T步内所有邻居做聚合(aggregate),且以固定的权重做聚合。这些经典的GNN方法只会根据拓扑信息选择邻居并聚合生成特征,不会过滤和筛选有价值的邻居。而我们不但要看拓扑信息还要看节点的行为特征。GeniePath关心在聚合的时候到底应该选取哪些重要的邻居信息、过滤那些不重要的节点信息。
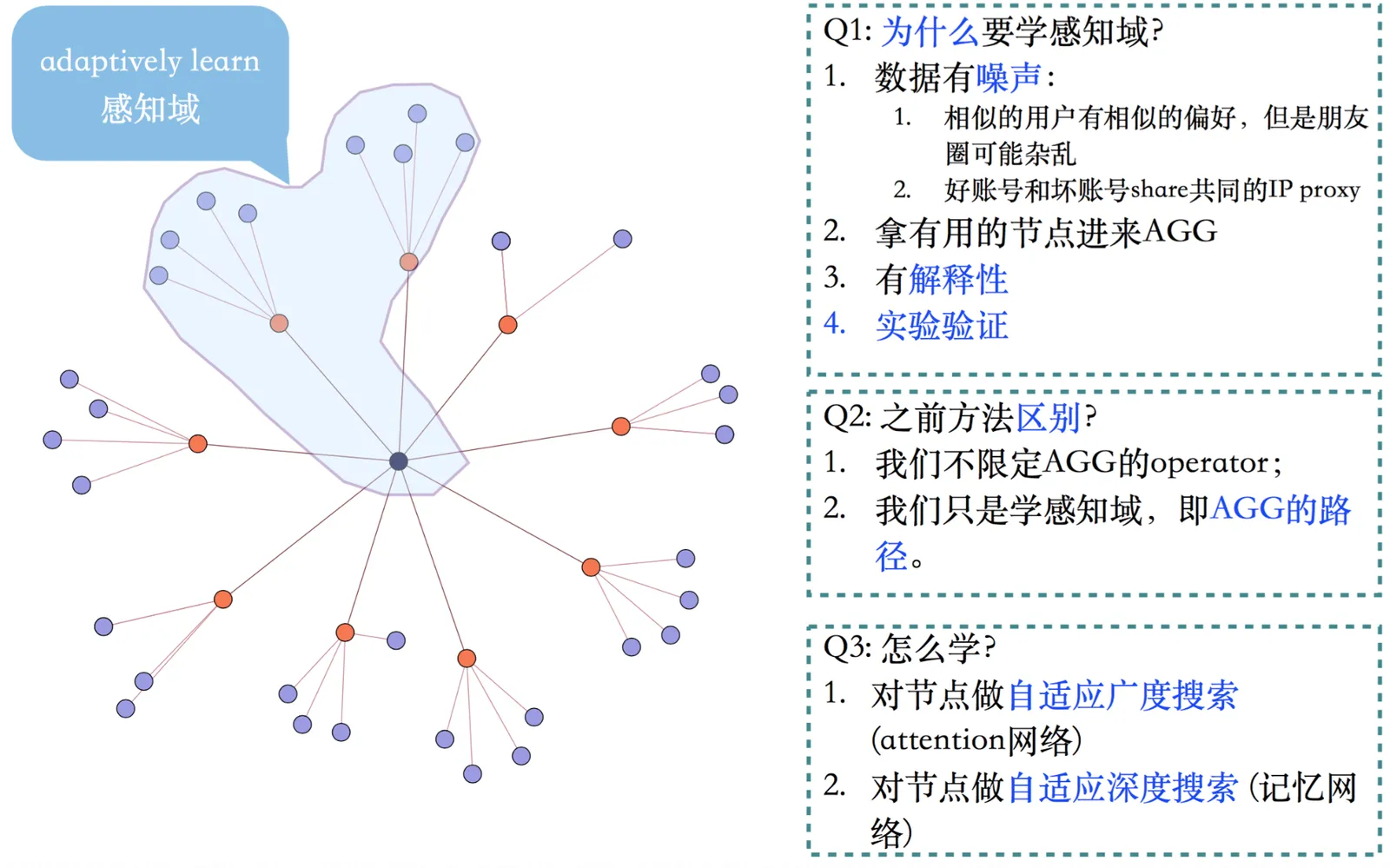
图:自适应的感知域示例
- 优点
1). 相比其他GNN算法,在大数据上可能有更好的性能,效率更高!
2). 可解释性更强。注意力权重可以区分出重要的边和次要的边,增加了可解释性。
- 实验
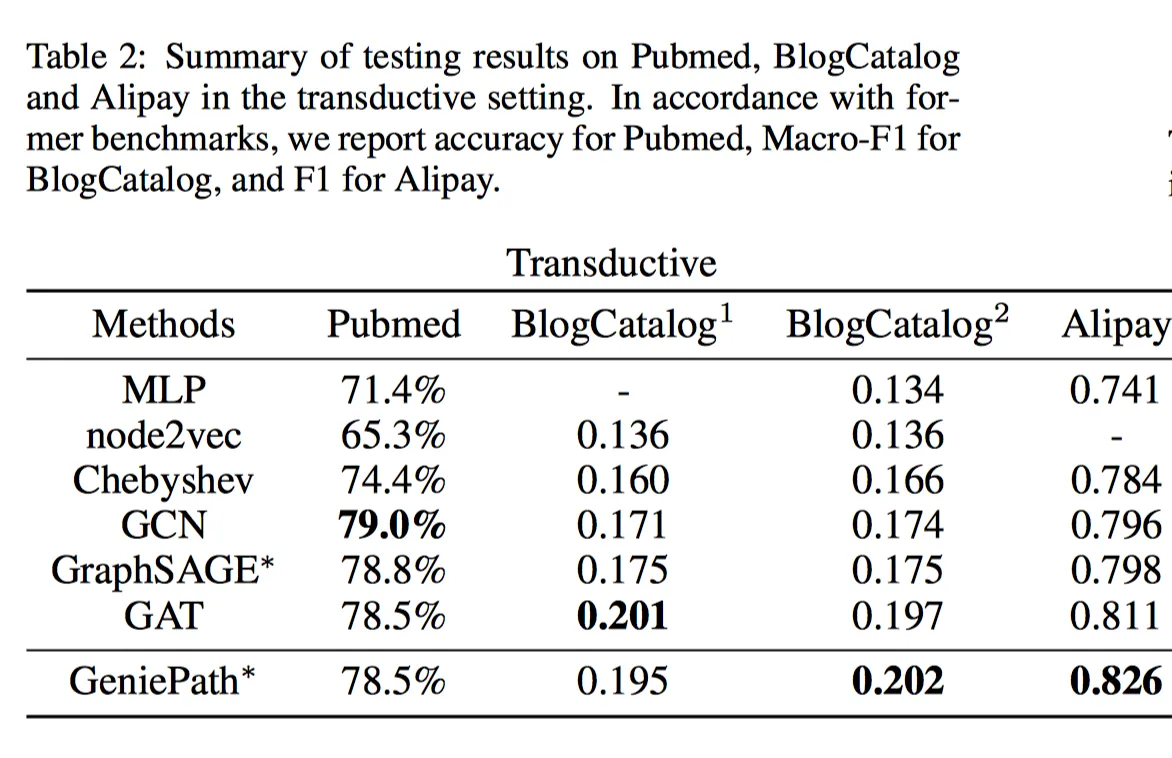
Alipay的数据集有1M节点,2M边,4k特征。可以看到数据集越大,效率越高,效果越好。
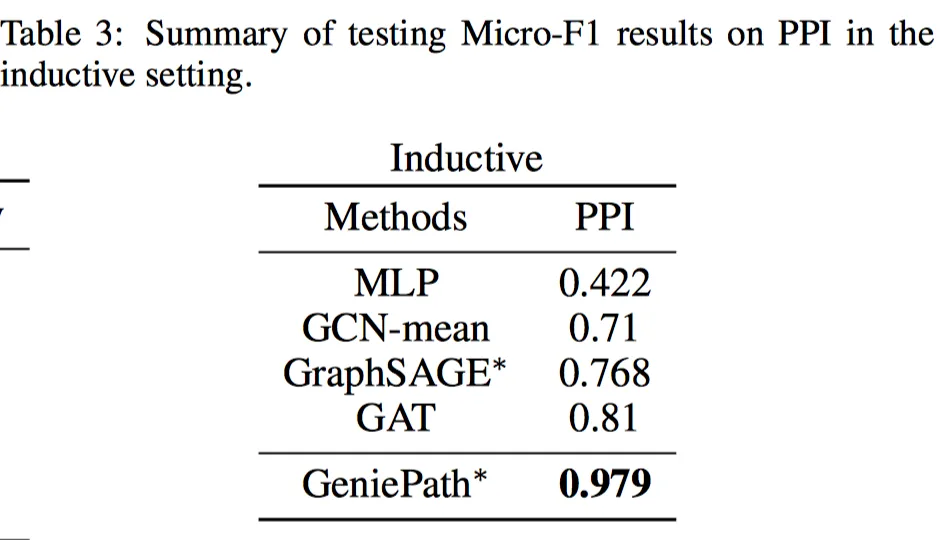
对蛋白质相互作用推理,F1值提升明显。
- 应用场景:
因为GeniePath是其他GNN算法的升级版,因此其他GNN算法的应用场景(比如前面讲到的Structure2Vec的应用场景)GeniePath应该都能实现,并且一般都可以期待更好的性能。GeniePath作为一个通用图神经网络算法已经在蚂蚁金服的风控场景实际使用,并得到较理想的效果,很好地提高了支付宝保护用户账户安全的能力[35]。其论文中还实现了的GeniePath应用场景包括:引用网络、BlogCatalog社交网络、蛋白质相互作用网络。
HeGNN
- 算法原理
GraphML团队开发的HeGNN[36]算法在GNN算法的基础上引入了多层次注意力机制。该算法支持异质图,即支持不同类型的节点和不同类型的边。过程可以简单理解为将不同类型的关系做成多个同质图,然后合并在一起。具体如下:
HeGNN算法使用了MetaPath(元路径)。每一条元路径携带着不同的语义,可以帮助我们利用异质信息网络中丰富的结构信息。比如消费图谱中的“User – (fund transfer) – User” (UU)记录了用户与用户之间的转账信息,“User-(transaction) -Merchant-(transaction)-User” (UMU)记录了两个用户同时在一个商家交易的信息。有效地融合这些元路径信息,可以使得模型充分利用不同类型的边的差异信息。下一个问题是如何有效地聚合异质的邻居信息。
层次注意力机制
直觉而言,不同的邻居、特征以及元路径会对节点的表示产生不同的影响。因此,下面介绍如何建模节点对这些方面信息的偏好。
邻居注意力
参照GAT算法的思想计算节点对每个邻居的注意力值,代表着每个邻居的贡献。可以按照如下的计算公式实现:


针对具体的场景,作者也给出了两种可替代的实现如下:
(1) avg-pool : 针对大规模的业务场景,可以直接对元路径下的邻居的特征做加权平均。这样可以大大降低计算量,而且一般可以得到一个不错的结果。

(2) geniepath-pool : 对于每一条元路径下的邻居,可以复用geniepath来实现单一元路径下的特征表示。
特征注意力
不同的特征可能对节点的表示存在不同的贡献。因此,参照文献,作者设计了如下的特征注意力层对每个特征点计算特征贡献值:


路径注意力
元路径抽取了节点在异质信息网络中的不同方面的信息,比如元路径“UU”抽取了用户的转账信息,元路径“UMU”抽取了用户的交易信息。所以需要设计路径的注意力层来捕获节点对不同元路径的偏好。具体地,按如下方式为每个节点计算它对元路径集合中每条元路径的注意力值 :
NCLF
NCLF [37](Neural Conditional Logic Field)是一种融合逻辑规则的推理算法。
我们知道神经网络的优点是学习能力强,但是需要的标注样本较多。而逻辑规则推理正好相反,它所需的标注样本少,但学习能力有限。NCLF的出发点是把这两者的优点融合,填补各自的缺点。
把专家经验引入到学习中来提高学习效率最近很火,专家经验可以转述为一阶逻辑,经典的解法是马尔可夫逻辑网络(MLN),并采用变分推断(VI)来加速求解,NCLF进一步引入GCN来近似后验。在实现的过程中我们使用Hinge-Loss Markov Random Fields(HL-MRF)进一步简化计算,将全举过程近似为一次性计算,使其更适用于工业大数据。为了减少GCN消息传播的衰减,引入了Loopy belief propagation。另外在构图上将二部图变为一般图。而引入规则之后,可以基于统计或学习得到规则权重,去掉坏规则可以进一步提高学习效果。在工程计算上,因为一阶逻辑的计算需要进行实例化(Grounding),计算量大,实际使用中需要进行分布式样本生成。
我们在公开数据集和业务规则数据上分别进行了效果对比。
KARI
KARI算法是我们基于ALPS的KGNN[38]框架延伸开发的算法框架。这里简要介绍其原理,详细内容可以查看KARI ATA文章[39]。本文前面介绍的传统的链接预测算法比如基于向量之间距离的Trans系列算法、基于语义匹配模型RESCAL系列算法、基于随机游走的node2vec系列算法,这些算法把嵌入向量作为参数通过学习来获得,在小规模图上能够取得不错的效果,但对于大规模图来讲,参数空间暴涨,难以落地。GraphML团队的KGNN框架提出将传统算法和GNN类算法相结合,就具有了共享参数这个优点。采用共享参数的聚合算子会极大降低参数空间,就能适用于大规模图推理。因此,为了充分挖掘大规模图谱中的结构信息以及充分学习图谱中丰富的异质信息导致的一对多、多对一、对称、非对称、相反、组合等关系,我们在Encoder-Decoder的思想下,Encoder选用GeniePath,Decoder选用DtransE,再结合自对抗负采样等能力结合而成了KARI算法。
Encoder-Decoder框架
KARI默认选取GeniePath为Encoder,默认选取DTransE为Decoder。KARI通过自监督学习生成节点和边的表达(Embeddings),可输出给下游模型使用,补充图结构特征。这里自监督学习是指标签数据不需要人工打标生成,利用边表中已知的三元组可以构成正样本,然后随机生成负样本,就构成了训练集。
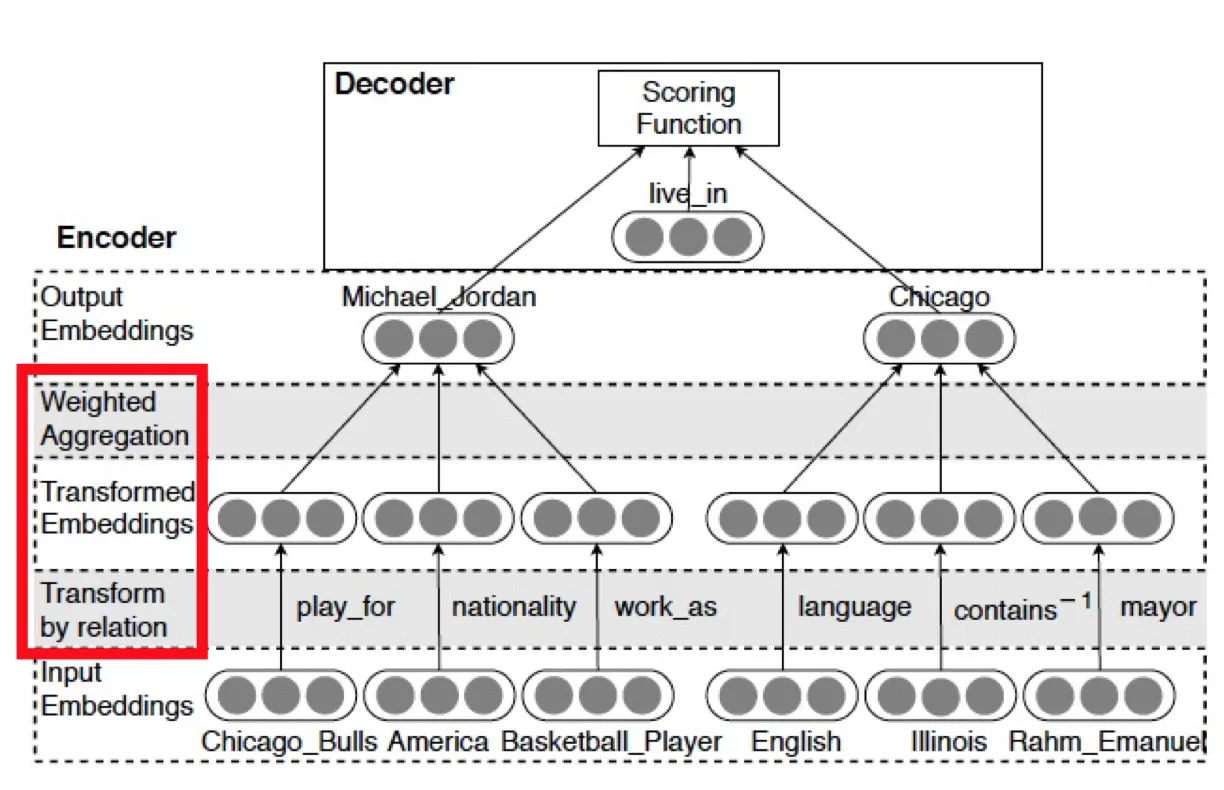
图:KARI的Encoder-Decoder框架示例
KARI目前支持的Encoder和Decoder如下:
- Encoder:GeniePath, GAT, GCN, Graphsage, Structure2Vec, Gin
- Decoder: DTransE, TransH, TransE, TransR, RESCAL, DistMult, Complex
下图中Encoder部分,中心节点A的嵌入向量是由其邻居节点B、C、D的信息聚合而来,而节点B、C、D的信息是由它们各自的邻居信息聚合而来,每一层汇聚就是一次迭代。这样我们通过Encoder中的T次迭代就获得了中心节点A的嵌入向量,重复这一过程还可以获得中心节点B的嵌入向量。关系r的嵌入向量最初由随机过程生成。然后将节点A、节点B和关系r的嵌入向量带入Decoder计算得分,再利用得分来计算loss。
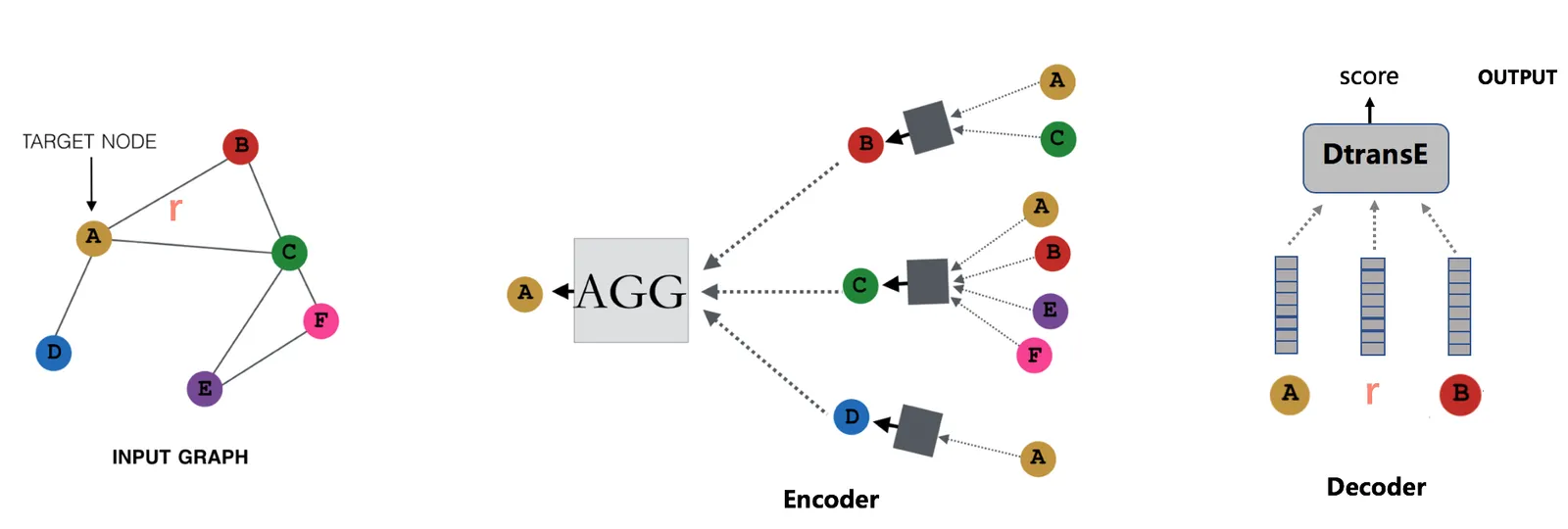
图:KARI的Encoder和Decoder示意图
Decoder的作用是将嵌入向量中的节点特征和图结构信息直观的表达为三元组的打分,该打分可以理解为三元组成立的“概率”。KARI的Decoder默认选择我们团队自研的DTransE算法。
KARI算法的特性总结如下:
- 能够充分融合图谱中点和边的属性信息以及图的结构信息
- 支持异质图谱,即多种类型的节点和边
- 支持1-N,N-1,N-N的复杂关系
- 支持对称/非对称、反转、组合关系
- 支持自我对抗负采样
- 模型共享参数能够支持大规模图推理
- 支持常见推理任务(实体相似度计算、链接预测、节点分类、社区发现等)
- 可自监督学习进行预训练,提取图谱的特征信息,生成节点和边的通用向量表达,输出给下游模型使用
KARI目前支持的业务包括:最终受益人UBO关系预测、可信关系降打扰、支付推荐、支付搜索、财富内容带货等等,并取得了较好的效果。
GraphSAINT
- 背景介绍
当数据有热点时,限制随机采样邻居个数这类做法可能导致采样到的邻居中有不重要的邻居,并且丢失了重要邻居的信息。特别是当我们需要计算多层邻居时,子图大小指数暴涨,难以计算。GraphSAINT[40]旨在解决稠密点的问题,它从根本上改变了采样方式。它不再在原图上采样邻居,而是从原图上采样一个子图下来,在这个子图上做局部的、完全展开的GCN。优点:
-
- 图变小了,计算效率高
- 效果好
- 前置采样,无需修改GCN模型
- 采样策略
采样策略倾向于影响大的节点被保留下来。采样概率只和链接信息有关,和节点特征无关。很适合提前预采样,下游GCN模型不用做改造。

上表给出了四种采样策略:
-
- Node sampler:第一步先采样节点得到一个节点子集,节点的采样概率正比于该节点的入度;第二步在该节点子集中补充好边。
- Edge sampler:第一步先采样边得到一个边的子集,边的采样概率反比于边的度(即反比于头节点和尾节点的度),然后将这些边涉及到的头、尾节点作为节点子集。
- Random walk sampler:第一步随机选择r个根节点开始随机游走h步;第二步将随机游走路径上的节点作为点的子集,边的子集就是这些点之间的边。
- Multi-dimensional random walk sampler:和方法c类似,区别是每步随机游走的概率正比于对应点的度。
- 消除分布偏差
GCN的通用表达式:
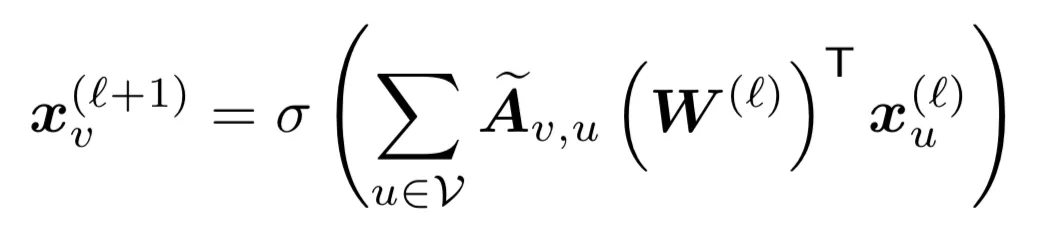
因为采样的图的分布和原图往往有差别,这会引入采样偏差。接下来的目的是尽量消除这个偏差。方法如下,采样以后中心节点的表达式修正如下:
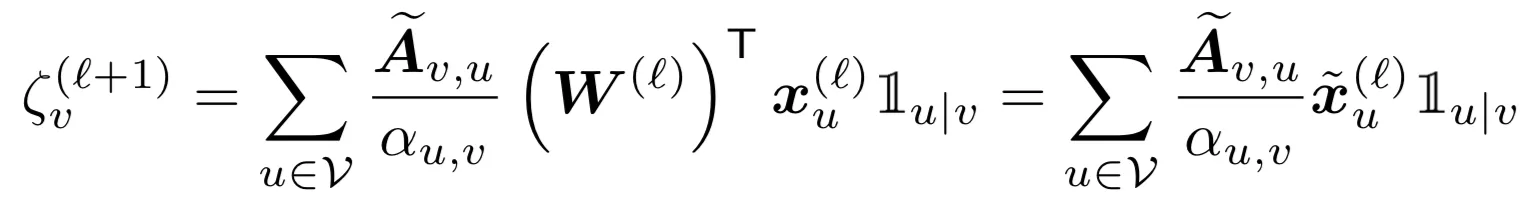
其中 和
和 是指当v被采样到的前提下,u被采样到的概率,二者概率的期望会互相抵消。这样就消除了采样的偏差。同理,在损失函数中也除以一个参数,消除采样偏差。
是指当v被采样到的前提下,u被采样到的概率,二者概率的期望会互相抵消。这样就消除了采样的偏差。同理,在损失函数中也除以一个参数,消除采样偏差。
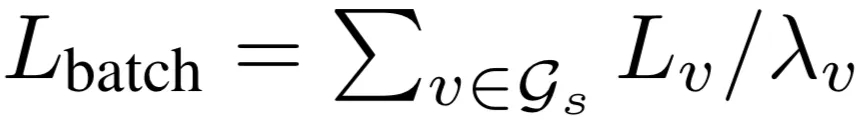
其中 指在一次采样图中采样到v的概率。
指在一次采样图中采样到v的概率。
- 实验结果
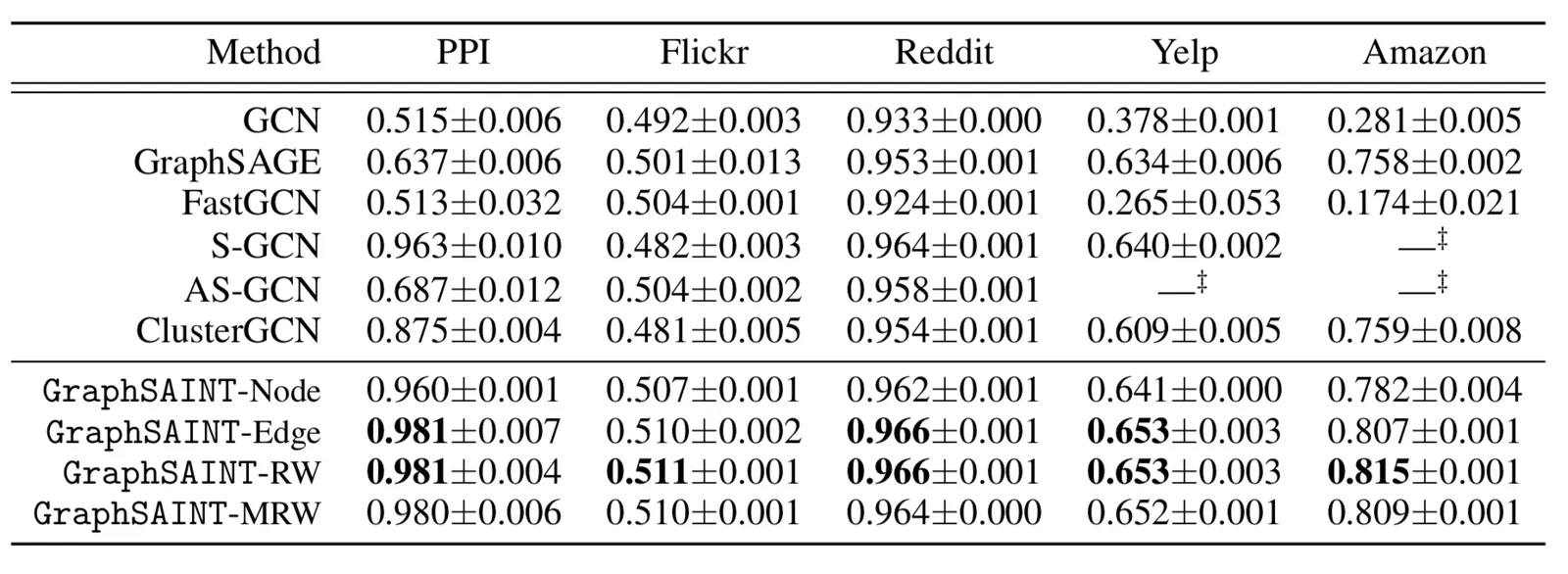
可以看到效果提升明显,特别是PPI数据集。而且效果比Cluster-GCN略有提升。GraphSAINT效果好的可能原因:
1.消除了噪音信息
2.朴素采样的GCN的mini-batch的方差较大,收敛性不好。
3.小图计算量小,可以训练更多个epoch
Cluster-GCN
- 算法介绍
Google开发的Cluster-GCN[41]算法,通过聚类形成一个个簇,并将链接尽量限制在簇内,起到了前置采样的效果。论文中介绍了两个算法方案,朴素版本的Vanilla cluster-GCN,和升级版本的Multiple cluster-GCN。下面分别介绍。
Vanilla cluster-GCN
该算法先做一次聚类,每个聚类的子图用来进行训练。聚类的目的是使簇内连接远大于簇间连接。图变小了,算法效果也不错。从热点角度来看相当于从多个热点中选出了少量几个热点作为簇,并隔离了不同的簇。该算法最大的优点是减小了batch之间的variance(偏差),效果提升,以及多层计算量呈线性而非指数增长。
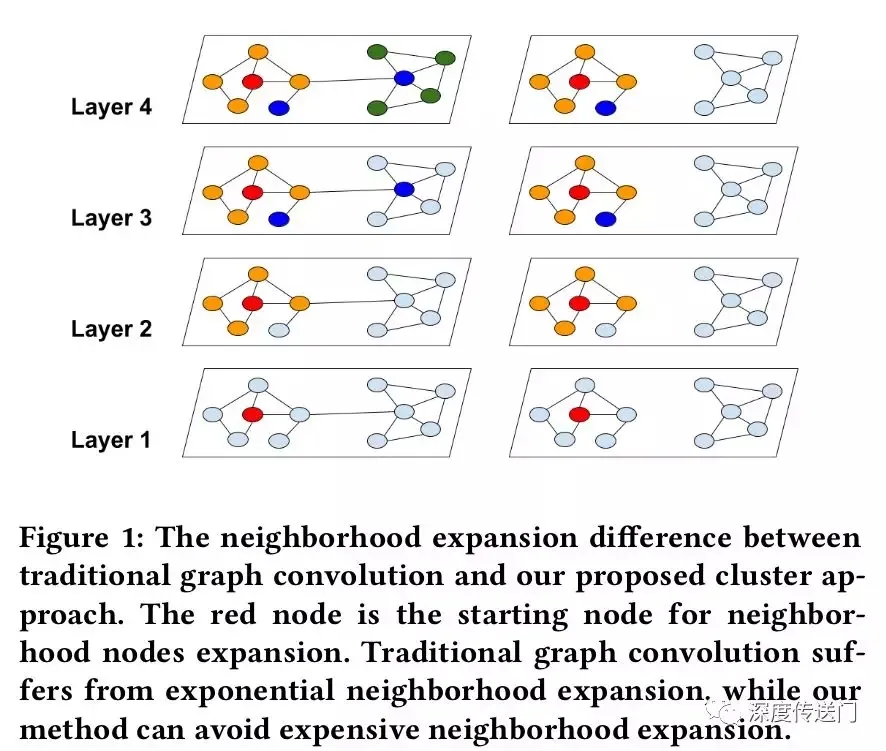

只保留对角处的矩阵,近似忽略非对角处的矩阵。其含义是保留簇内的连接,忽略簇间的连接。对于Vanilla cluster-GCN,每个簇对应一个batch。这样导致计算效率增加,计算精度提高。效率增加是因为随着层数增加,节点数量呈线性增长,而其他GCN呈指数增长;精度增加其解释是减小了batch间的Variance(偏差),以及增加了计算层数。
Multiple cluster-GCN
尽管朴素Cluster-GCN实现了良好的时间和空间复杂度,但仍然存在两个潜在问题:
- 图被分割后,一些连接被删除。因此性能可能会受到影响。
- 图聚类算法往往将相似的节点聚集在一起,因此聚类的分布可能不同于原始数据集,从而导致在执行SGD更新时对 full gradient的估计有偏差。
为了解决上述问题,文中提出了一种随机多聚类方法,在簇接之间进行合并,并进一步减少batch间的偏差(variance)。作者首先用一个较大的p把图分割成p个簇V1,…,Vp,然后对于SGD的更新重新构建一个batch B,也就是一个batch中有多个簇。随机地选择q个簇,定义为t1,…,tq ,并把它们的节点包含到这个batch B中。此外,在选择的簇之间的连接也被添加回去。作者在Reddit数据集上进行了一个实验,证明了该方法的有效性。
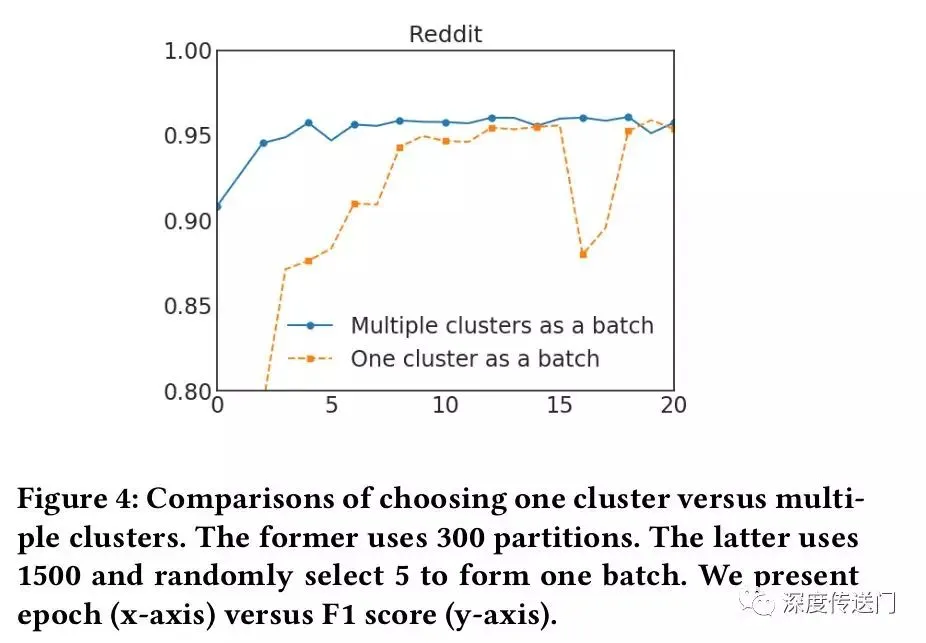
- 实验结果
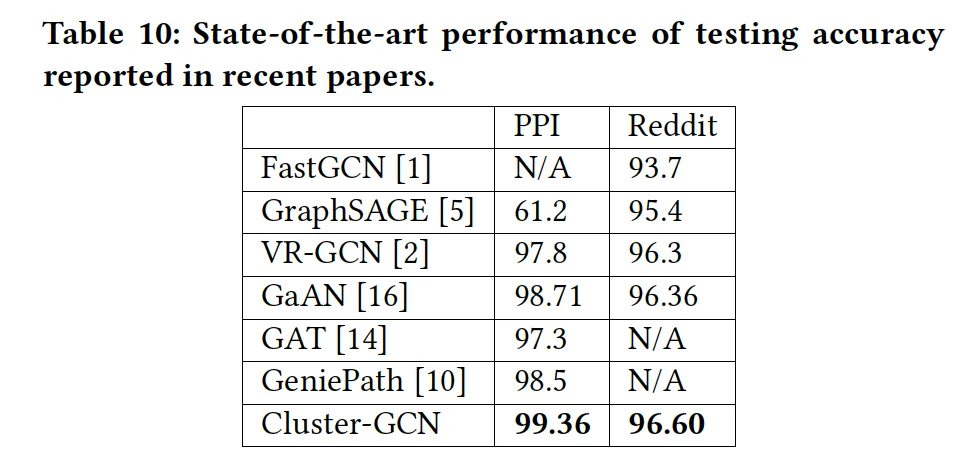
实验中在两个公开数据集上达到了State-of-art的效果。
讨论
从算法分类角度
- 有监督、无监督
无监督:Deepwalk、Node2Vec、Metapath2vec、LINE、Louvain
有监督:GCN(半监督)、GraphSAGE、SDNE(半监督)、GeniePath、GAT、Structure2Vec、HeGNN
- 异质图、同质图
支持异质图:HeGNN、metaPath2vec、KGNN
支持同质图:Deepwalk、Node2Vec、LINE、SDNE、GCN、GraphSAGE、GeniePath、GAT、Structure2Vec
从应用角度
- 链接预测
所有的embedding算法都支持链接预测。有一个区别是同质图模型支持一种关系预测,而异质图模型支持多种关系预测。(另外加上ALPS平台尚未包括的trans系列也可以做链接预测)。
- 实体归一(相似度服务器托管网计算)
所有的embedding算法都支持相似度计算。相似度是由具体的任务目标来定义并体现在loss中,一般的任务目标有距离相似性(两个节点有几度相连)、结构相似性、节点类型相似性(label预测)。
- 属性值预测(label预测)
GCN、GraphSAGE、GeniePath、GAT、Structure2Vec、HeGNN等。
持续分享 SPG 及SPG +LLM双驱架构相关干货及进展
官网:https://spg.openkg.cn/
Github:https://github.com/OpenSPG/openspg
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
相关推荐: 前端树形Tree数据结构使用-🤸🏻♂️各种姿势总结
01、树形结构数据 前端开发中会经常用到树形结构数据,如多级菜单、商品的多级分类等。数据库的设计和存储都是扁平结构,就会用到各种Tree树结构的转换操作,本文就尝试全面总结一下。 如下示例数据,关键字段id为唯一标识,pid为父级id,用来标识父级节点,实现任…

