系统可靠性是系统在规定的时间内及规定的环境条件下完成规定功能的能力,也就是系统无故障运行的概率。这里的故障是系统行为与需求的不符,故障有等级之分。
系统故障模型
系统故障是指由于部件的失效、环境的物理干扰、操作错误或不正确的设计引起的硬件或软件中的错误状态。错误(差错)是指故障在程序或数据结构中的具体位置。错误与故障位置之间可能出现一定距离。故障或错误有如下几种表现形式:
(1)永久性。描述连续稳定的失效、故障或错误。在硬件中,永久性失效反映了不可恢复的物理改变。
(2)间歇性。描述那些由于不稳定的硬件或变化着的硬件或软件状态所引起的、仅仅是偶然出现的故障或错误。
(3)瞬时性。描述那些由于暂时的环境条件而引起的故障或错误。
故障模型是对故障的表现进行抽象,可以建立如下4个级别的故障模型。
(1)逻辑级的故障模型。逻辑级的故障有固定型故障、短路故障、开路故障和桥接故障。固定型故障是指电路中元器件的输入或输出等线的逻辑固定为0或固定为 1,如某线接地、电源短路或元件失效等都可能造成固定型故障;短路故障是指一个元件的输出线的逻辑值恒等于输入线的逻辑值,元件的开路故障是元件的输出线悬空,逻辑值可根据具体电路来决定;桥接故障是指两条不应相连的线连接在一起而发生的故障。
(2)数据结构级的故障。故障在数据结构上的表现称为差错。常见的差错有独立差错(一个故障的影响表现为使一个二进制位发生改变)、算术差错(一个故障的影响表现为使一个数据的值增加或减少 和单向差错(一个故障的影响表现为使一个二进制向量中的某些位朝一个方向改变)。
(3)软件故障和软件差错。软件故障是指软件设计过程造成的与设计说明的不一致软件故障在数据结构或程序输出中的表现称为软件差错。与硬件不同,软件不会因为环境应力而疲劳,也不会因为时间的推移而衰老。因此,软件故障只与设计有关。常见的软件差错有非法转移、误转移、死循环、空间溢出、数据执行和非法数据。
(4)系统级的故障模型。故障在系统级上的表现为功能错误,即系统输出与系统设计说明的不一致。如果系统输出无故障保护机构,则故障在系统级上的表现就服务器托管网会造成系统失效。
一般来说,故障模型建立的级别越低,进行故障处理的代价也越低,但故障模型覆盖的故障也越少。如果在某一级的故障模型不能包含故障的某些表现,则可以用更高-级的模型来概括。
系统可靠性模型
与系统故障模型对应的就是系统可靠性模型,本节简单介绍三种常用的可靠性模型。
1.时间模型
时间模型基于这样一个假设:一个软件中的故障数目在 t=0时是常数,随着故障被纠正,故障数目逐渐减少。在此假设下,一个软件经过一段时间的调试后剩余故障的数目可用下式来估计

其中,为调试时间,Er()为时刻 软件中剩余的故障数,E0为=0时软件中的故障数,Ec()为在[0,]内纠正的故障数,I为软件中的指令数。由故障数 Er()可以得出软件的风险函数Z(t)=C*Er(),其中 C是比例常数。于是软件的可靠度为

软件的平均无故障时间为

在时间模型中,需要确定在调试前软件中的故障数目,这往往是一件很困难的任务。
2.故障植入模型
故障植入模型是一个面向错误数的数学模型,其目的是以程序的错误数作为衡量可靠性的标准。故障植入模型的基本假设如下。
(1)程序中的固有错误数是一个未知的常数
(2)程序中的人为错误数按均匀分布随机植入。
(3)程序中的固有错误数和人为错误被检测到的概率相同。
(4)检测到的错误立即改正。
用M表示固有错误数,m表示植入的错误数,n表检测到的错误数,其中检测到的植入错误数为k,用最大似然法求解可得固有错误数M的点估计值为

3.数据模型
在数据模型下,对于一个预先确定的输入环境,软件的可靠度定义为在 n 次连续运行中软件完成指定任务的概率。其基本方法如下。设需求说明所规定的功能为 F,而程序实现的功能为 F‘,预先确定的输入集为{ei: i=1, 2,…,n),令导致软件差错的所有输入的集合为 Ee。,即Ee={ej: e∈andF(ej) ≠ F'(ej)},则软件运行一次出现差错概率为

一次运行正常的概率为 R1 =1-P1。
在上述讨论中,假设所有输入出现的概率相等。如果不相等,且ej出现的概率为Pi(i=1,2,n),则软件运行一次出现差错的概率为
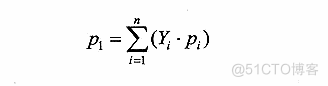
于是,软件的可靠度(n 次运行不出现差错的概率)为

显然,只要知道每次运行的时间,上述数据模型中的R(n)就很容易转换成时间模型中的R(t)。
可靠性指标与评估
在 上节讨论了系统可靠性的模型,那么,究竟如何来评估一个系统的可靠性呢?这就是本节要介绍的内容。
可靠性指标
与可靠性相关的概念主要有平均无故障时间、平均故障修复时间以及平均故障间隔时间等。
1.平均无故障时间
可靠度为R(0)的系统的平均无故障时间(Mean TimeTo Failure,MTTF)定义为从0时到故障发生时系统的持续运行时间的期望值,计算公式如下

如果R()=et,则MTTF=1/。为失效率,是指器件或系统在单位时间内发生失效的预期次数,在此处假设为常数。
例如,假设同一型号的 1000 台计算机,在规定的条件下工作 1000小时,其中有10台出现故障。这种计算机千小时的可靠度R 为(1000-10)*1000=0.99,失效率为 10/(1000X1000)=1X10-5)。因为平均无故障时间与失效率的关系为 MTTF=1/,因此MTTF=10小时。
2.平均故障修复时间
可用度为A(t)的系统的平均故障修复时间(Mean Time ToFix,MTTR)可以用类似于求 MTTF 的方法求得。设 A1(t)是在风险函数 Z(t)=0 且系统的初始状态为 1状态的条件下A(t)的特殊情况,则

此处假设修复率 u(t)=/(常数),修复率是指单位时间内可修复系统的平均次数,则
MTBF=MTTR+MTTF
在实际应用中,一般M服务器托管网TTR 很小,所以通常认为 MTBFZMTTF
可靠性计算
计算机系统是一个复杂的系统,而且影响其可靠性的因素也非常繁复,很难直接对其进行可靠性分析。但通过建立适当的数学模型,把大系统分割成若干子系统,可以简化其分析过程。
1.串联系统
假设一个系统由n 个子系统组成,当且仅当所有的子系统都能正常工作时,系统才能正常工作,这种系统称为串联系统,如图所示。

设系统中各个子系统的可靠性分别用R1,R2,…,Rn表示,则系统的可靠性R=R1*R2*…*Rn)。
如果系统中各个子系统的失效率分别用1,2…n, 来表示,则系统的失效率=1+2+…+n
2.并联系统
假如一个系统由n个子系统组成,只要有一个子系统能够正常工作,系统就能正常工作,如图 所示。
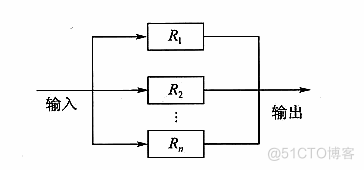
设系统中各个子系统的可靠性分别用R1,R2,,Rn表示,则系统的可靠性R=1-(1-R1)X(1-R2)X…X(1-Rn)。
假如所有子系统的失效率均为,则系统的失效率为,即

在并联系统中只有一个子系统是真正需要的,其余 n-1个子系统称为冗余子系统随着冗余子系统数量的增加,系统的平均无故障时间也增加了。
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: Python爬虫与数据挖掘在外汇市场分析中的应用
外汇市场是全球最大的金融市场之一,每天的交易量可以达到几万亿美元。深入了解外汇市场的趋势和变化对于投资者来说至关重要,因为即使是微小的价格波动也可能导致巨额利润或损失。从过去的历史数据中抽取经验教训,并使用数据挖掘算法来预测未来趋势,已成为投资者在外汇市场中获…

