Local Spectral Graph Convolution For Point Set Feature
Wang等人(2018)
对k-NN中的点之间的联合关系进行建模。联合学习k-NN中所有点的特征的卷积核将捕获与点的几何布局相关的拓扑信息,以及与输入点样本本身相关的特征,例如,颜色、纹理或其他属性。
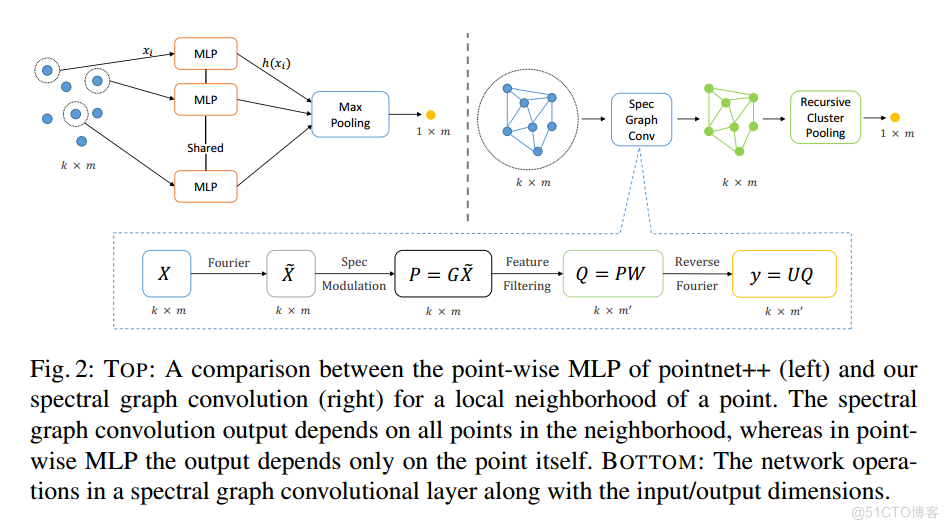
谱图卷积以联合的方式考虑局部邻域中的所有点,结合了相邻点的特征以及图拓扑中编码的结构信息。这是通过图傅立叶变换和光谱调制步骤来实现的,这些步骤使用图拉普拉斯算子的本征空间来混合邻域特征。
在本文中,我们建议在pointnet++框架中利用谱图cnn的功能,同时采用不同的池化策略。这使我们能够解决目前基于点云的深度学习方法的两个局限性:1)对于每个点样本,特征的学习都是以孤立的方式在局部邻居间进行的。2)以后层的信息聚合使用贪婪的赢者通吃的最大池化策略。相反,我们采用了不同的池化模块,如图1中的示例所示。此外,与现有的谱图CNN方法相比,我们的方法不需要预计算[3,4]。我们将局部光谱特征学习与递归聚类和池化相结合,为从无组织点云中提取点集特征提供了一种新的架构。
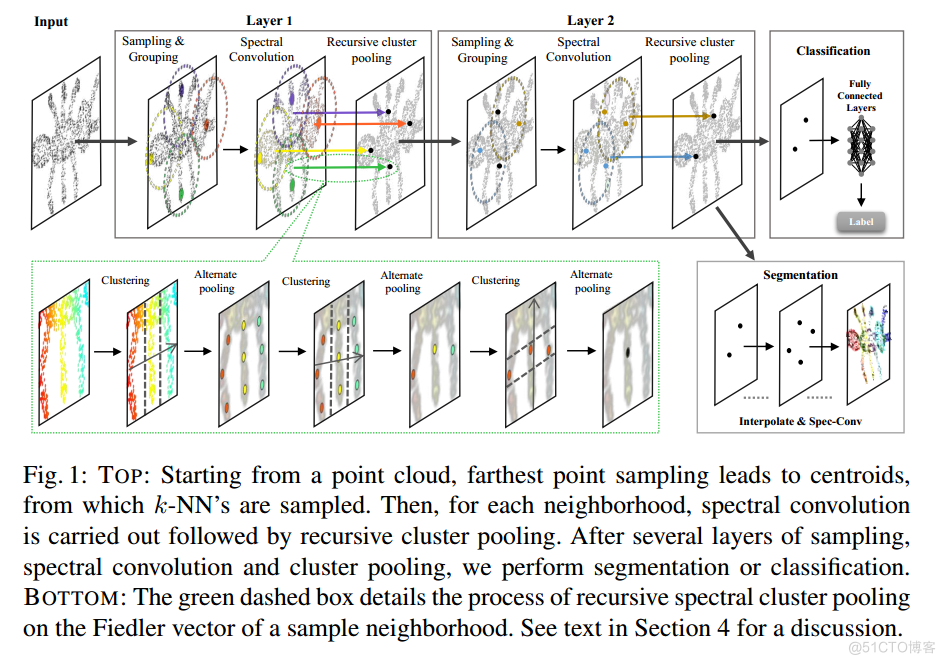
TOP:从点云开始,最远点采样导致质心,k-NN从质心采样。然后,对每个邻域进行谱卷积,然后进行递归聚类池化。经过多层服务器托管网采样、谱卷积和聚类池化,我们进行分割或分类。BOTTOM:绿色虚线框详细描述了对样本邻域的费德勒向量进行递归光谱聚类池化的过程。请参阅第4节中的讨论。
pointnet++框架中特征学习的局限性:1:以孤立的方式学习点的k个近邻(k- nn)的特征。在pointnet++中,k-NN中每个点的单独特征用h(xi), i∈1,2,…, k。不幸的是,这个隐藏层函数不能模拟k- nn中点之间的联合关系。
2:pointnet++的k-NN的集合激活函数是通过对每个点的隐藏层的输出进行最大池化来实现的,最大池化不允许保存来自邻域内不相交的点集的信息。
本文的组合点集特征提取操作可归纳为
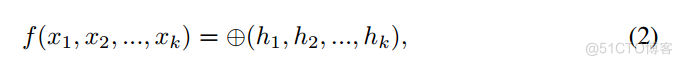
其中hi是卷积输出h(x1, x2,…), xk)在第i点处求值,⊕表示我们的集合激活函数。
图中顶点的卷积运算:
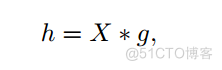
其中X表示输入点集特征,g表示图卷积核。
这相当于图谱域中的一个逐元素的Hadamard积,如Defferrard等[3]和Shuman等[5]所示:

这里的~ X表示点集特征的图傅里叶变换,g ~表示图傅里叶域中的滤波器,~ h表示滤波服务器托管网后的输出。为了在原始(顶点)域中获得滤波后的输出,需要进行傅里叶反变换。
局部邻域的图形式:
在局部邻域中给定k个点的集合x1, x2,…,xk,建立一个表示图Gk,其顶点V为点,其边E∈V V的权值为a: E→R * +,表示特征空间中顶点之间的成对距离。
这提供了一个k k的非负对称图邻接矩阵a,其条目Aij = dist(xi, xj)。然后,我们基于这个邻接矩阵计算图的频谱,并执行图的傅里叶变换,频谱滤波,最后进行傅里叶反变换。
图傅里叶变换
为了计算点特征X∈R km的图的傅里叶变换,这是Gk顶点上的图信号,我们首先需要计算归一化图拉普拉斯:
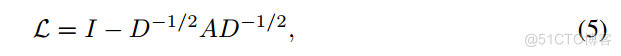
其中I为单位矩阵,D∈R kk为对角度矩阵,其项Dii为对应矩阵A每行的和。由此可知,L是一个实对称正半定矩阵,并且有一组完备的组成图的傅里叶基的正交特征向量
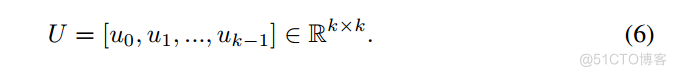
特征值可以用来构造对角矩阵
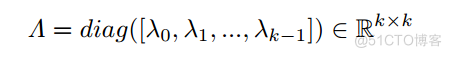
它包含了图的频率。得到L = UUT。然后将X的傅里叶变换定义为~ X = U T X,其逆定义为X = UX ~。
光谱滤波
卷积运算在傅里叶域中定义为
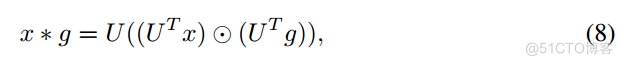
其中⊙为逐元Hadamard积,x为任意图信号,g为空间滤波器。如果我们定义y = x * g作为图卷积的输出,则可以得到经g过滤的图信号x∈R km可以写成
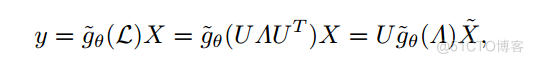
其中表示任意参数化
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
sql2005有个函数ISNUMERIC(expression)函数:当expression为数字时,返回1,否则返回0。这只是一个菜鸟级的解决办法,大多数情况比较奏效。 eg: select ISNUMERIC(‘123’) –结果为1 但是,该函数有个缺…

