1 Laplacian 算子
给定无向图(G=(V, E)),我们在上一篇博客《谱图论:Laplacian二次型和Markov转移算子》中介绍了其对应的Laplacian二次型:
]
这里(f: Vrightarrow mathbb{R})为图的顶点标签,(usim v)表示服从均匀分布的随机无向边((u, v)in E)。直观地理解,Laplacian二次型刻画了图的“能量”(energy)。(mathcal{E}[f])的值越小,也就意味着(f)更加“光滑”(smooth),即其值不会沿着边变化得太剧烈。
事实上,我们可以做进一步地等价变换:
mathcal{E}[f] &=frac{1}{2} cdot mathbb{E}_{u sim v}left[(f(u)-f(v))^2right]\
&= langle f, f rangle – mathbb{E}_{usim v}left[f(u)f(v)right]\
&= langle f, f rangle – langle f, Kf rangle\
&= langle f, If – Kf rangle \
&= langle f, (I – K) f rangle
end{aligned}
]
这(K)为我们在上一篇博客中提到的MarKov转移算子,它满足:((K f)(u)=mathbb{E}_{v sim u}[f(v)])。
对于最后一个等式而言,我们称算子
]
为图(G)的 (归一化)Laplacian算子。
注 对于(d)-正则图(G)而言,我们有
[L = I – frac{1}{d} A = frac{1}{d}(dI – A)
]这里(A)为(G)的邻接矩阵,(dI – A)被称为非归一化Laplacian算子,或直接被简称为Laplacian算子。
和(K)一样,(L)也是定义在函数空间(mathcal{F}={f: V rightarrow mathbb{R}})上的线性算子,按照以下规则将(fin mathcal{F})映射到(Lfin mathcal{F}),满足
]
通过研究(L),我们就能把握Laplacian二次型(mathcal{E}[f] = langle f, Lf rangle)的特性,从而把握图(G)的特性,这是谱图理论中至关重要的一点。
接下来再来看我们熟悉的那个示性函数例子。
例 设图顶点的子集(Ssubseteq V), 0-1示性函数(f=mathbb{I}_S)用于指示顶点是否在集合(S)中,即:
1 & text { if } & u in S \
0 & text { if } & u notin S
end{array}right.
]
则我们有:
& langle f, Lf rangle = mathbb{E}[f] = text{Pr}_{usim v}[uin S, vnotin S]\
& langle f, frangle = mathbb{E}_{usim pi}[f(u)^2] = text{Pr}_{usim pi}[uin S] = text{vol}(S)
end{aligned}
]
直观地理解,这里(text{Pr}_{usim v}[uin S, vnotin S])表示“伸出”(S)的边占总边数的比例;(text{vol}(S))表示(S)的“体积”。则上述两式的比值
frac{langle f, Lfrangle}{langle f, f rangle} &= text{Pr}_{usim v}left[vnotin Smid u in S right]\
&= text{Pr}left[ underbrace{text{pick a random } uin S}_{text{proportional to the degree}}text{, do } 1 text{ step, that you get out of } S right] \
& in left[0, 1right]
end{aligned}
]
表示从集合(S)中的“逃出”概率。我们将这个比值称为(S)的电导(conductance)(我们在博客《图数据挖掘:重叠和非重叠社区检测算法》中介绍过,当时是用来衡量社区划分的质量,这个值越小说明划分得越好),用(Phi[S])表示。
2 再论Laplacian二次型的极值
有了(L),那么最小化/最大化(mathcal{E}[f])的问题就可以进行进一步的研究了。考虑下列优化问题:
& max quad mathca服务器托管网l{E}[f] = langle f, Lfrangle = underbrace{frac{1}{2}mathbb{E}_{usim v}left[left(f(u) – f(v)right)^2right]}_{text{continous func. } f: spacemathbb{R}^nrightarrow mathbb{R}}\
& text{s.t.} underbrace{quad lVert f rVert^2_2 = langle f, frangle = mathbb{E}_{usimpi}[f(u)^2] = 1}_{text{compat set}, text{ ellipsoid in } mathbb{R}^n} quad (Leftrightarrowtext{Var}[f] = 1)
end{aligned}
]
存在一个极大值点(varphi: Vrightarrow mathbb{R}),它满足:
]
也即(Lvarphi parallel varphi)。此外,该极大点也可以被有效地找到。
推论
]
事实
& mathbb{E}[varphi] = mathbb{E}_{usim pi}left[varphi(u)right] = mathbb{E}_{usim pi}left[varphi(u) cdot 1right] = 0 Leftrightarrow langle varphi, mathbb{1} rangle = 0 Leftrightarrow varphi perp mathbf{1}\
& text{Var}[varphi] = 1
end{aligned}
]
下面我们来证明为什么(mathcal{E}[f])的极大值点(varphi)满足(Lvarphi parallel varphi)。
证明 我们采用反证法,即假设极大值点(varphi)满足(Lvarphi nparallel varphi),如下图所示:
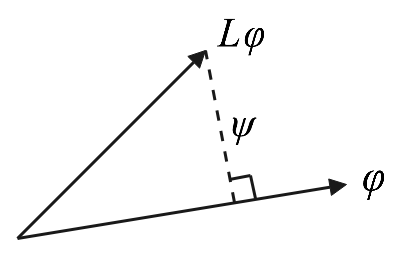
由于(Lvarphi nparallel varphi),那么我们可以现在(Lvarphi)与(varphi)之间的垂线方向上取(f = varphi + varepsilon psi)((varepsilonneq 0)是一个很小的数,(psi)为单位向量),根据勾股定理有(lVert f rVert^2_2 = 1 + epsilon^2)。则:
mathcal{E}[f] = langle f, Lf rangle &overset{(1)}{=} langle varphi + varepsilon psi, Lvarphi + Lvarepsilon psi rangle \
& overset{(2)}{=} langle varphi, L varphi rangle + underbrace{varepsilon langle phi, L psi rangle + varepsilon langle psi, L varphi rangle}_{L text{ is self-adjoint}} + varepsilon^2 langle psi, L psi rangle\
& overset{(3)}{=} langle varphi, L varphi rangle + underbrace{2varepsilon langle psi, L varphi rangle}_{>0} + mathcal{O}(epsilon^2) \
& > langle varphi, L varphi rangle
end{aligned}
]
(其中等式((3))用到了自伴算子的定义)而这与(varphi)为极大值点相矛盾。因此,(mathcal{E}[f])的极大值点(varphi)满足(Lvarphi parallel varphi)。
3 Laplacian算子的谱性质
在上一小节,我们已经证明了(varphi)是一个极大值点。现在我们不采用(varphi)及所有与(varphi)平行的解,而将解限制在与(varphi)相正交的子空间中。这样,优化问题就变为了:
]
求解该优化问题可以采用与之前相同的思路,也即存在极大值点(varphi^{prime})满足:
]
这里(lambda^{prime} 的原因是(lambda)已经对应了极大值点,而我们添加了新的约束使(fnparallel varphi),故这里(lambda^{prime})对应的是第二大的极值点。
重复这个步骤,不断寻找第3大,第(4)大……的极大值点,并使其与之前找到的所有极大值点正交,直到找到最后一个(第(n)大的)极大值点。在这个过程中得到的极大值点都会(perp)于(mathbf{1})((mathbf{1})为全1向量),而最后一个极大值点即为所剩的(mathbf{1})向量本身,此时有
]
由此可见最后一个特征值(最小的特征值)为0。
通过上面所述的步骤,我们可以找到Laplacian算子的(n)个相互正交的规范化特征向量(范数为1)及其对应的特征值。而这事实上和我们在线性代数课程中所学过的谱定理密切相关。
谱定理 若(T)为一个实向量空间(V)上的自伴算子,则(V)有一个由(T)的特征向量组成的规范正交基(orthonormal basis)(varphi_1, varphi_2, cdots, varphi_{n}),每个特征向量分别对应于实特征值(lambda_1, lambda_2, cdots, lambda_{n})。
我们前面证明过Markov转移算子(K)是自伴的,则(L = I – K)也是自伴的(事实上,又由于(langle f, Lf rangle geqslant 0),(L)还是半正定的)。于是,关于图(G)的Laplacian算子就有以下定理:
定理 给定(G)及其Laplacian算子(L),则存在规范正交基(函数)(mathbf{1} equiv varphi_1, varphi_2, cdots, varphi_{n})及实数$0=lambda_1 leqslant lambda_2leqslant cdots leqslant lambda_{n} leqslant 2 $满足:
]
我们将(lambda_2)和更广泛的(lambda_k)((k)为一个较小的值)称为低频(low-frequency) 特征值,而将(lambda_n)称为高频(high-frequency) 特征值。
事实上,除了讨论Laplacian算子(L)之外,我们也可以讨论Markov转移算子(K)的特征向量及特征值。由(L = I – K),我们有
]
则(K)拥有特征向量(varphi_i)及其相伴的特征值 (kappa_i = 1 – lambda_i),且(-1leqslant kappa_{n}leqslantcdotsleqslant kappa_2 leqslant kappa_1 = 1)。
定义 给定(f: Vrightarrow mathbb{R})和正交基(varphi_1, varphi_2, cdots varphi_{n}),那么(f)能够唯一地表示为(varphi_i)的一个线性组合:
]
这个性质会为我们带来许多新的结论。
命题 将(L)应用于(f),就得到了:
]
可以看到,(L)应用于(f)可以转换为分别去应用于正交基。为了方便,我们常常会使用如下所示的记号:
]
此外,我们也可以使用规范正交基来简化我们内积和范数的表示。
命题 给定另一个函数
]
则(f)和(g)的内积
]
推论
根据内积我们可以诱导出范数
]
(f)的均值可表示为:
]
可以看到,(f)沿规范正交基的展开式中的第一项就是均值乘单位向量:
]
(f)的方差可表示为:
text{Var}[f] & = mathbb{E}[f^2] – mathbb{E}[f]^2 \
& = sum_{1leqslant i leqslant n} left[hat{f}(i)^2right] – hat{f}(1)^2 \
&= sum_{1
(注意第(1)项(hat{f}(1)^2 – hat{f}(1)^2)抵消掉了)
Laplacian二次型(mathcal{E}[f])可表示为:
mathcal{E}[f] &= langle f, Lf rangle \
&= sum_{i, j}lambda_i hat{f}(i)hat{f}(j)langle varphi_i, varphi_j rangle\
&= sum_{1
(注意第(1)项由于(lambda_1=0)就消失了)
参考
[1] CMU 15-751: TCS Toolkit
[2] Bilibili: CMU计算机科学理论(完结)—你值得拥有的数学和计算机课)
[3] Spielman D. Spectral graph theory[J]. Combinatorial scientific computing, 2012, 18: 18.
[4] Axler S. Linear algebra done right[M]. springer publication, 2015.
2023-10-19 00:24
orion-orion
阅读(10)
评论(0)
编辑
收藏
举报
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net

