连续信源的熵
由于连续信源信号幅度取值无限性, 要精确表示这样的信号, 理论上需要无穷个bit才行。即连续信源的绝对熵为 $infty$ 。
仿照离散信源熵的定义, 有连续信源的熵(相对熵)定义为
$$
H(X)=-int_{-infty}^{infty} f(x) log (f(x)) d x
$$
其中 $f(x)$ 为连续信源信号 $mathbf{X}$ 的概率密度函数。连续信源的 (相对) 熵可正可负。
R(D) 的定义域
率失真的定义域问题就是在信源和失真函数已知的情况下,讨论允许平均失真度 $bar{D}$ 的最小和最大取值问题。
由于平均失真度 $bar{D}$ 是非负实数 $dleft(x_{i}, y_{j}right)$ 的数学期望, 因此 $bar{D}$ 也是非负的实数,即 $bar{D} geq 0$ , 故 $bar{D}$ 的下界是 0 。允许平均失真度能否达到其下限值0, 与单个符号的失真函数有关。
$D_{min }$ 和 $Rleft(D_{min }right)$
信源的最小平均失真度:
$$
D_{min }=sum_{i=1}^{n} pleft(x_{i}right) min _{j} dleft(x_{i}, y_{j}right)
$$
只有当失真矩阵的每一行至少有一个 $mathbf{0}$ 元素时,信源的平均失真度才能达到下限值 $mathbf{0}$ 。
当 $boldsymbol{D}_{text {min }}=mathbf{0}$ , 即信源不允许任何失真时,信息率至少应等于信源输出的平均信息量一信息熵。
$$
R(0)=H(X)
$$
对于连续信源
$$
Rleft(D_{min }right)=lim _{D rightarrow 0} R(D) rightarrow infty
$$
因为实际信道总是有干扰,其容量有限,要无失真地传送连续信息是不可能的。
当允许有一定失真时, $R(D)$ 将为有限值, 传送才是可能的。
$mathbf{R}(mathbf{D})$ 的定义域为 $[D_{text {min }}, D_{text {max }}]$ 。
- 通常 $D_{text {min }}=0, quad Rleft(D_{min }right)=H(X)$
- 当 $D geq D_{text {max }}$ 时, $quad R(D)=0 $
- 当 $0 leq D leq D_{text {max }}$ 时, $0lt R(D)lt H(X)$
由于 $I(X, Y)$ 是非负函数,而 $R(D)$ 是在约束条件下的 $I(X, Y)$ 的最小值, 所以 $R(D)$ 也是一个非负函数, 它的下限值是零。
$$
boldsymbol{R}(D) geq 0
$$
$D_{text {max }}$ :是定义域的上限。
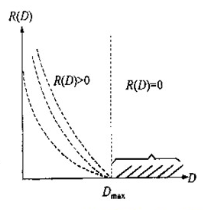
$D_{text {max }}$ 是满足 R(D)=0 时所有的平均失真度中的最小值。
$$
D_{text {max }}=min _{R(D)=0} D
$$
由于 $I(X, Y)=0$ 的充要条件是 X 与 Y 统计独立, 即:
$$
begin{array}{c}
pleft(y_{j} mid x_{i}right)=pleft(y_{j}right) \
D_{max }=min _{pleft(y_{j}right)} sum_{i} sum_{j} pleft(x_{i}right) pleft(y_{j}right) dleft(x_{i}, y_{j}right) \
=min _{pleft(y_{j}right)} sum_{j} pleft(y_{j}right) sum_{i} pleft(x_{i}right) dleft(x_{i}, y_{j}right) \
D_{max }=min _{j=1,2 cdots m} sum_{i=1}^{n} pleft(x_{i}right) dleft(x_{i}, y_{j}right)
end{array}
$$
例: 设输入输出符号表为 $mathbf{X}=mathbf{Y}={mathbf{0}, 1}$ , 输入概率分布 $p(x)={1 / 3,2 / 3}$ , 失真矩阵
$$
d=left[begin{array}{ll}
0 & 1 \
1 & 0
end{array}right]
$$求 $mathbf{D}_{min }$ 和 $mathbf{D}_{max }$
解:失真矩阵的每一行至少有一个 0 元素时, $D_{min }=0$
$$
begin{array}{l}
D_{max }=min _{j=1,2} sum_{i=1}^{2} p_{i} d_{i j} \
=min _{j}left(frac{1}{3} times 0+frac{2}{3} times 1, frac{1}{3} times 1+frac{2}{3} times 0right) \
=min _{j}left(frac{2}{3}, frac{1}{3}right)=frac{1}{3}
end{array}
$$例: 设输入输出符号表为 $mathbf{X}=mathbf{Y}={mathbf{0}, mathbf{1}}$ , 输入概率分布 $p(x)={1 / 3,2 / 3}$ , 失真矩阵
$$
d=left[begin{array}{ll}
1 / 2 & 1 \
2 & 1
end{array}right]
$$求 $D_{min }$ 和 $mathbf{D}_{text {max }}$
解:
$$
begin{array}{l}
D_{min }=sum_{i=1}^{n} pleft(x_{i}right) min _{j} dleft(x_{i}, y_{j}right) \
=frac{1}{3} times frac{1}{2}+frac{2}{3} times 1=frac{5}{6} \
D_{max }=min _{j=1,2} sum_{i=1}^{2} p_{i} d_{i j}=min _{j}left(frac{1}{3} times frac{1}{2}+frac{2}{3} times 2, frac{1}{3} times 1+frac{2}{3} times 1right) \
=min _{j}left(frac{3}{2}, 1right)=1 \
end{array}
$$
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net

