本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
有失真信源编码的数学模型如下图所示，将编码过程看成信息经过有扰信道传输的过程。信道输出 Y 即为编码输出。
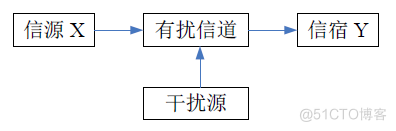
对离散信道，用信道转移概率（条件概率）p(y|x)表示信道。
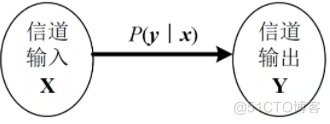
如BSC信道：
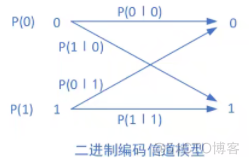
互信息
设有两个随机事件X和Y ,
- X取值于信源发出的离散消息集合
- Y取值于信宿收到的离散符号集合
如果信道是无噪的,当信源发出消息 
后,信宿必能准确无误地收到该消息, 彻底消除对 的不确定性, 所获得的信息量就是 的自信息 
，即 本身含有的全部信息。
一般而言，信道中总是存在着噪声和干扰，信源发出消息 ，通过信道后, 信宿只可能收到由于干扰作用引起的某种变形 
。(例如BSC信道，可能发出0收到1)
- 信宿收到 后推测信源发出 的概率
称为后验概率。 - 信源发出消息 的概率
称为先验概率。
互信息定义
定义为 的后验概率与先验概率比值的对数
**互信息 
表示接收到某消息 后获得的关于事件 的信息量。**单位和自信息相同。
例 、某地二月份天气构成的信源为:
求得自信息量分别为
若得知 “今天不是晴天” ，作为收到的消息 
当收到 后, 各种天气发生的概率变成后验概率:
表明从 分别得到了 
各 1 比特的信息量。 消息 使 的不确定度各减少 1 bit。
互信息的性质
- 互易性
- 当事件
, 
统计独立时, 互信息为 0 , 即 
- 互信息可正可负
- 任何两事件之间的互信息不可能大于其中任一事件的自信息(见上述公式3)
例：设 e 表示事件“降雨”， f 表示事件“空中有乌云”，且 𝒑（𝒆）=𝟎.𝟏𝟐𝟓，𝒑（𝒆|𝒇）=𝟎.𝟖
求：
- 事件“降雨”的自信息
- 在“空中有乌云”条件下，“降雨”的自信息
- 事件“无雨”的自信息
- 在“空中有乌云”条件下，“无雨”的自信息
- “降雨”与“空中有乌云”的互信息
- “无雨”与“空中有乌云”的互信息
解:
表示 “无雨”, 则
= 1- p(e) = 0.875 ,
= 1-
= 0.2
故:
说明事件 “空中有乌云” 不利于事件 “无雨” 的出现。
参考文献：
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.
服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.e1idc.net
