集成电路仿真器（SPICE）的实现原理

　　本文系统地介绍类SPICE集成电路仿真器的实现原理，包括改进节点分析（MNA）、非线性器件建模、DC/AC分析、时域/（复）频域仿真以及涉及的数值方法。
　　基于本文原理，实现了SPICE-like仿真器：https://github.com/cassuto/CSIM

1 理论基础

　　任何集总参数电路都能依据基尔霍夫电流定律（KCL）、基尔霍夫电压定律（KVL）和支路约束方程建立模型并通过解析法或数值法求解，进而实现计算机辅助电路分析（CACA，Computer Aided Circuit Analysis）。

　　CACA核心：

　　1. 建立电路数学模型：

• a）拓扑约束：利用图论分析电路，建立KCL、KVL方程。常见方法包括割集电压法、节点分析（NA, Nodal Analysis）法和C.W. Ho(^{[1]})提出的改进节点分析（MNA, Modified Nodal Analysis）法等。UC Berkeley开发的SPICE即采用MNA方法(^{[7]})。
• b）元件约束：根据元件的物理特性和分析的目标建立VCR约束。（复）频域分析可使用s域模型或相量（正弦稳态）模型建立VCR约束；时域分析则可用微分代数方程（DAE）建立VCR约束，或先使用s域模型求解最后进行Laplace逆变换。

　　2. 求解数学模型。主要有解析法和数值法两种。并非所有模型都容易找到解析解。常采用数值方法，对于线性方程组，可用LU分解法等；对于非线性方程，需通过迭代法将其线性化。对于微分方程，常使用数值积分。

　　3. 分析模型。主要进行误差和灵敏度分析。

　　CACA把上述过程总结为一套算法，让计算机自动完成。

2 术语约定

在不同参考资料中，相关术语的定义各有差别。本文统一采用如下规定：

• 网络（Network）：描述电路拓扑的无向图（带参考方向时为有向图），用(G(V,E))表示；
• 网表（Netlist）：网络的一个实例；
• 端子（Pin）：元件的接线处；
• 端口（Port）：一对端子构成一个端口；
• 节点（Node）：连接两个或两个以上端子的交汇点；
• 支路（Branch）：对于一个二端元件，若两个端子分别接在节点(s)和(t)上，则该二端元件构成一条支路((s,t) in E)；
• 关联（Associative）：给定节点(n)，如果存在支路((s,t) in E)满足(s=n)或(t=n)，就称该支路与节点(n)关联；
• 回路（Circuit）：如果从节点(n_0)出发，能沿与之关联的支路(b_0)到达节点(n_1)，再以(n_1)为起点，重复上述过程并最终返回节点(n_0)，并且形成的访问序列()没有重复的节点，则该序列指出一个回路；

3 改进节点分析（MNA）前置内容

　　MNA是节点分析（NA）的增广，这里先介绍NA，如果您对此熟悉可以跳过本节。

3.1 NA方程的推导

　　我们从拓扑学角度推导NA方程。

　　将电路抽象为网络。首先为网络中各支路指定电流参考方向，使其成为有向网络，设其关联矩阵为：(mit{A}_{n times b} = begin{bmatrix} a_{jk} end{bmatrix} = begin{cases} 1, & text{支路k参考电流从节点j流出}\ -1, & text{支路k参考电流从节点j流入} \ 0, & text{支路k与节点j无关联} end{cases})

　　其中(n)为节点个数，(b)为支路个数。

　　设支路电压向量为(mit{U}=begin{bmatrix} u_1, u_2, cdots ,u_b end{bmatrix} ^mathrm{T})；支路电流向量为(mit{I}=begin{bmatrix} i_1, i_2, cdots ,i_b end{bmatrix} ^mathrm{T})。

　　根据KCL定律(^{[2]})：

　　其中(mit{I}_s=begin{bmatrix} i_{s_1}, i_{s_2}, cdots ,i_{s_n} end{bmatrix} ^mathrm{T})为注入电流，(i_{s_j}>0)表示电流注入节点(j)，反之表示电流流出节点(j)。

　　设节点电压向量为(mit{U}_n=begin{bmatrix} u_{n_1}, u_{n_2}, cdots ,u_{n_n} end{bmatrix} ^mathrm{T})。在网络中任意选定一个节点作为参考节点，对于余下((n-1))个节点，规定节点电压为该节点相对于参考节点的电位差。

　　根据KVL定律(^{[2]})：

　　设支路导纳矩阵为：

　　通过导纳描述支路约束方程：

　　将式((ref{NA_KVL}))代入式((ref{NA_BRAN}))，得到：

　　再将式((ref{NA_KVL_BRAN}))代入式((ref{NA_KCL}))中，得到：

　　令(mit{Y} = mit{A}mit{G}mit{A}^mathrm{T})，最终得到节点分析方程：

　　其中(mit{Y})称为节点导纳矩阵。

　　给定网表可计算节点导纳矩阵(mit{Y})，也可由电流源支路确定(mit{I}_s)（若无，置0）。最后只需解上述线性代数方程组，即可得出节点电压(mit{U_n})。

3.2 节点导纳矩阵的物理意义

　　上节已经推出节点导纳矩阵的表达式：

　　按照关联矩阵的定义，若支路(k)与节点(i)或(j)无关联，则(a_{ik}a_{jk}=0)。若支路(k)与节点(i)与(j)均有关联，则(a_{ik}=pm 1)且(a_{jk}=mp 1)，此时有(a_{ik}a_{jk}=begin{cases} -1 & (i ne j) \ 1 & (i = j) end{cases})。

　　由此可知，(sumlimits_{k=1}^{b} g_k cdot (a_{ik}a_{jk}) =y_{ij} space (i ne j))的物理意义为：若节点(i)与节点(j)之间有直接关联的支路（(i ne j)），则(y_{ij})就是两节点(i)和(j)之间关联的所有支路的导纳之和取负数，否则(y_{ij}=0)。把它定义为互导(y_{ij} space (i ne j))。
　　(sumlimits_{k=1}^{b} g_k cdot (a_{ik}a_{ik})=y_{ii})的物理意义为：(y_{ii}=sumlimits_{j=1 \ j neq i}^{n} y_{ij})，即所有与节点(i)直接关联的支路的导纳之和，把它定义为自导(y_{ii})。

　　于是节点导纳矩阵就能简单表示为：

　　下面以一个实例来说明这种表示的好处：

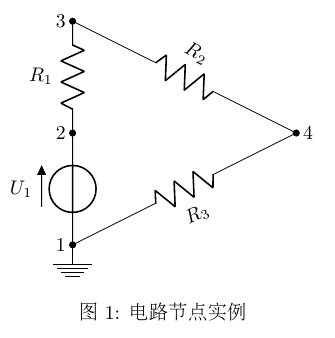
　　按照自导和互导的物理意义，就能直接知道节点1的自导(y_{11})为(R_3)和(U_1)的电导之和，节点1到2的互导(y_{12})为(U_1)的电导取负数，其它同理，可直接得出节点导纳矩阵如下：

　　需要注意(y_{1,3}=y_{3,1}=0)，(y_{2,4}=y_{4,2}=0)，因为节点1和3、2和4之间没有直接关联的支路。另外，因为U1是理想电压源，(G_{U_1}=infty)，因此这个电路用NA无法直接求解，这个例子揭示了NA的局限性。

4 改进节点分析（MNA）的原理

　　节点分析（NA）直接处理含无伴电压源（内阻为0）的支路时会遇到困难，因为这些支路的导纳为无穷大，方程无法求数值解。上文图1中的(U_1)就属于这种情况。

　　MNA解决NA局限性的思路很简单：对NA方程组进行增广。NA只分析节点电压，而MNA能同时分析支路电流，将两种状态变量混合在一起求解。

　　MNA混合方程如下：

　　其中(mit{Y})是节点导纳矩阵；(mit{U})是节点电压向量；(mit{I})是节点电流向量，对应方程(mit{Y}mit{U}=mit{I})与NA无异。此外，(mit{J})是支路电流向量，(mit{B})、(mit{C})、(mit{D})、(mit{E})是新增加的方程的系数矩阵。

　　这些系数矩阵用“橡皮图章”法（Rubber Stamps）机械地生成(^{[1]})，实现电路分析的程序化。

4.1 方程生成算法

　　C.W. Ho提出的元件橡皮图章算法（Element Rubber Stamps）(^{[1]})可以根据网表直接生成各子矩阵的值。算法初始时(mit{Y}=mit{B}=mit{C}=mit{D}=mit{I}=mit{E}=0)。遍历网表中所有元件，每遇到一个元件(e)，就将该类型元件对应的贡献值(c(e))加到相应的子矩阵，遍历结束时各子矩阵就有了正确的值，从而直接产生方程组。因为每种元件的贡献值是常量，可以将贡献值编制成表格，也称为“表格法”。

　　在稍后的推导中可以看到，算法“将贡献值加到对应子矩阵”的的理论依据是线性电路的叠加性。MNA本来只能处理线性电路，但是稍后可以看到如何利用线性化处理非线性电路。

　　方程生成算法可以描述为：

　　算法的关键是贡献值(c_Y(e))、(c_B(e))、(c_C(e))、(c_D(e))、(c_I(e))、(c_E(e))。

　　下面推导了一些常见一端口和二端口线性元件的贡献值。

4.2 常见一端口线性元件对Y、B、C、D、I、E的贡献

　　假设一端口元件所在支路为(k)，电压与电流取关联参考方向(s rightarrow t)。

4.2.1 阻抗元件

　　设元件导纳为(y)，支路约束方程为：

　　其中(i_k)为元件所在支路电流。

　　整理上式得：

　　对应MNA矩阵形式为：

　　如果多个阻抗元件并入支路，则支路的导纳就是它们之和。因此每当一个阻抗元件并入支路(s rightarrow t)时，只需在MNA方程的分块矩阵Y中加上导纳：

即加上贡献值：

4.2.2 独立电压源（VS）

　　设VS的电压值设定为(e_s)。支路约束方程为：

　　其中(i_k)为VS所在支路的电流。

　　对应MNA矩阵形式为：

　　如果多个电压源串在同一支路，则支路电压为它们之和，因此每当一个VS串入支路(s rightarrow t)时，只需加上贡献值：

4.2.3 独立电流源（CS）

　　设CS电流值设定为(i_k)，支路约束方程为：

　　如果多个电流源并入支路，则支路总电流就是它们之和，因此每当一个CS并入支路(s rightarrow t)时，只需加上贡献值：

　　上述这些例子其实反映了线性电路的叠加性。这就是为什么任何元件加入电路时都只需在MNA对应矩阵加上贡献值。

4.3 常见二端口线性元件对Y、B、C、D、I、E的贡献

　　假设元件的端口1所在支路为(k)，电压与电流取关联参考方向(s rightarrow t)；端口2所在支路为(c)，电压与电流取关联参考方向(p rightarrow q)。

4.3.1 电压控制电压源（VCVS）

　　设VCVS电压放大倍数为(mu)，控制电压为((u_p – u_q))。支路约束方程为：

　　其中(i_k)为VCVS受控端口所在支路的电流。

　　对应MNA矩阵形式为：

　　可知每当一个VCVS加入支路(s rightarrow t)、(p rightarrow q)时，贡献为：

4.3.2 电压控制电流源（VCCS）

　 设VCCS的转移电导为(g)，控制电压为((u_p – u_q))。支路约束方程为：

　　对应MNA矩阵形式为：

　　可知每当一个VCCS加入支路(s rightarrow t)、(p rightarrow q)时，贡献为：

4.3.3 电流控制电压源（CCVS）

　　设CCVS的转移电阻为(r)，控制电流为(i_c)，支路约束方程为：

　　其中(i_k)为CCVS受控端口所在支路电流。

　　对应MNA矩阵形式为：

　　可知每当一个CCVS加入支路(s rightarrow t)、(p rightarrow q)时，贡献为：

4.3.4 电流控制电流源（CCCS）

　　设CCCS的电流放大倍数为(alpha)，控制电流为(i_c)。支路约束方程为：

　　对应矩阵形式为：

　　可知每当一个CCCS加入支路(s rightarrow t)、(p rightarrow q)时，贡献为：

5 稀疏矩阵计算

　　对于线性电路，按照上述方法可以建立MNA方程：

　　直接采用高斯列主元素消元法、LU分解法、雅各比迭代法等都能求解上述方程，具体参考教科书[3]。

　　但是，求解稠密矩阵方程需要(O(n^3))的时间。如果观察到电路对应的系数矩阵(mit{A})是稀疏矩阵，就可以使用更优化的算法，因为而稀疏矩阵中存在大量零元素，利用稀疏矩阵算法，存储和计算时都可以跳过大量零元素，从而使算法所需的时间和空间大幅减少。

6 非线性元件的分析

　　MNA可以方便地分析线性电路，但无法直接处理非线性电路。

　　幸运的是，如果利用迭代法将非线性元件线性化，使每一步迭代都能用等效的线性元件替代，就能利用MNA分析和求解非线性电路。SPICE就采用这种方法(^{[7]})。

6.1 牛顿-拉夫逊法求解非线性MNA方程

　　牛顿-拉夫逊法（Newton-Ralfsnn’s method）是最常用求解非线性方程近似根的算法。

　　牛顿-拉夫逊法通过如下迭代格式计算非线性方程(f(mit{x}) = mit{0})的近似根(mit{x})：

　　根据MNA方程((ref{MNA}))，设

　　根据式((ref{equ:newtown_fx}))：

　　这其中涉及的雅克比矩阵有：

　　利用雅可比矩阵将式((ref{equ:newtown_fx}))改写为：

　　再将式((ref{equ:fMNA}))代入，整理可得迭代格式：

　　即(mit{A}'(mit{x}^{(k)}) cdot mit{x}^{(k+1)}=mit{z}'(mit{x}^{(k)}))，可见迭代格式与线性代数方程组形式保持一致。给定初值(mit{x}^{(0)})，计算(mit{A}'(mit{x}^{(0)}))、(mit{z}'(mit{x}^{(0)}))，然后求解线性代数方程组，得到(mit{x}^{(1)})，再将(mit{x}^{(1)})作为新的初值，重复上述过程，生成迭代序列({mit{x}^{(k)}})，直到(|mit{x}^{(k+1)} – mit{x}^{(k)}|)小于设定的误差限时，可认为迭代收敛，取近似根(tilde{mit{x}} = mit{x}^{(k+1)})。

　　牛顿-拉夫逊迭代的本质是将非线性问题分成若干线性问题，这就启发我们用该方法实现元件的线性化，从而允许用MNA分析非线性元件。

6.2 理想PN结模型

　　理论上任何非线性元件都可以用动态电压源或电流源等效代替。为了便于应用MNA，这里使用动态电流源代替。

　　设理想PN结位于支路(s rightarrow t)上，理想PN结电流的近似方程为：

　　其中(I_0)为反向饱和电流，(U_T)为温度电压当量，这两个参数都是由物理特性决定的。

　　将PN结作为动态电流源注入支路(s rightarrow t)，根据独立电流源支路的结论((ref{equ:cs_contrib}))，有：

　　代入牛顿-拉夫逊迭格式((ref{equ:mna_newtown_format}))：

　　对比之前推出的阻抗元件支路的结论（式(ref{equ:mna_y_comp})），可以认为((ref{equ:pn_newtown_left}))描述的是等效电阻，其电导({g_d}^{(k)})随迭代次数(k)动态变化，然而在本轮迭代内是不变的，可视作线性元件：

　　再考虑式((ref{equ:mna_newtown_format}))，右边式子可展开为：

　　其中：

　　从物理意义上看，式((ref{equ:PN_i_d}))描述的是动态电流源(i_d)与动态电阻(g_{eq})并联，如图2所示，这样就实现了元件的线性化，每次迭代都可以用MNA分析了。

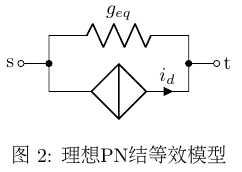
　　至此式((ref{equ:mna_newtown_format}))左右两边都已确定，得到MNA方程组：

　　每当一个理想PN结加入支路(s rightarrow t)时，只需对子矩阵作如下更新：

　　值得注意的是整个求解过程是迭代进行的，每轮迭代都要重新计算等效电路的参数并重新求解MNA，即：

　　给定初值(mit{x}^{(0)})（这其中包含PN结两端的节点电压({u_s}^{(0)})、({u_t}^{(0)})），代入式((ref{equ:pn_newtown_left}))和式((ref{equ:pn_newtown_right}))可得线性代数方程组((ref{equ:new_rn_mna}))，解线性代数方程组可以得到(mit{x}^{(1)})，再将(mit{x}^{(1)})作为新的初值，如此迭代。当相邻两次迭代获得的解(mit{x}^{(k+1)})与(mit{x}^{(k)})满足(| mit{x}^{(k+1)}-mit{x}^{(k)} | lt epsilon)时，就可认为迭代收敛，可以取近似解(mit{x}^{(k+1)})。

　　下面给出了非线性电路分析的算法流程。

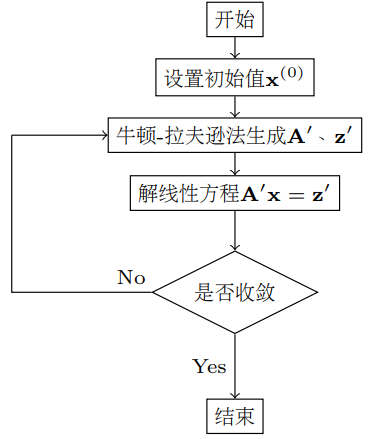
6.2.1 收敛性问题

　　在PN结特性方程的牛顿-拉夫逊迭代中，存在如下图所示的异常情况：

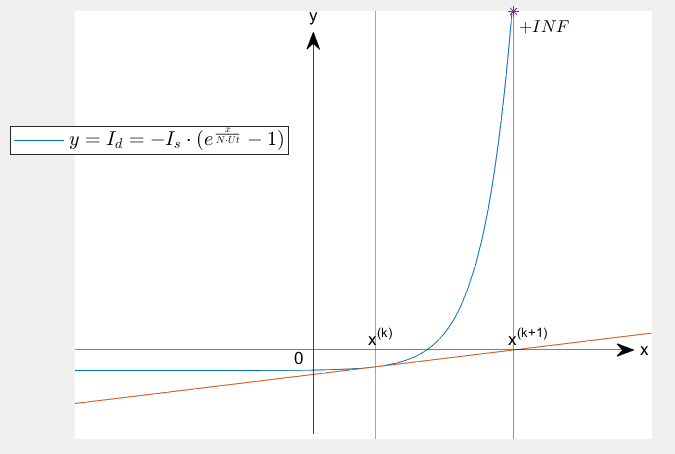
　　图中第(k+1)步迭代时，由于指数函数的迅猛增长，(i_d^{(k+1)})超出机器数所能表示的范围，产生上溢，使得迭代无法进行下去。

　　考虑到实际电路中不可能出现如此大的电流（双精度浮点数最大值约为(10^{308})）；另外在结电流方程中，当(y)急剧增长时，(x)的变化范围却很小。因此可以将PN结电压限制在较小范围内，以避免数值溢出(^{[6]})。

　　PN结临界电压是V-I曲线中曲率半径最小的点，当PN结电压大于临界电压时，结电流开始急剧增加，因此可用PN结临界电压(U_{th})作为阈值的参考。

　　一种最简单的阈值限制算法是(x’= max(x, 10U_{th}))，将结电压限制在(10U_{th})以下，但限制后的V-I曲线在(U_d=10U_{th})处的导数不存在，大于(10U_{th})后导数为0，造成不收敛。

　　SPICE中的限制算法(^{[7]})更合理，当(U_d > U_{th})时，采用以电流(I_d)为变量的迭代（解决反函数）；当(U_d le U_{th})时，采用正常的迭代格式。

6.3 收敛条件

　　对于MNA方程中的节点电压(U)和支路电流(J)，SPICE采用独立的收敛条件。设(xi_r)为相对误差限，(xi)为绝对误差限。当：

　　并且，当(|J^{(k+1)} _b- J^{(k)}_b| le xi_r cdot J_{b,max} + xi)时，认为迭代收敛。

　　其中(U_{n,max}=max(|U^{(k+1)}_n|, |U^{(k)}_n|))；(U^{(k+1)}_n, U^{(k)}_n)为相邻两次迭代的结果。(J_b)同理。

7 直流扫描分析（DC Sweep）

　　至此，我们搭建的框架可以实现SPICE的第一个应用——直流扫描分析，即遍历参数，输出各参数下电路的静态工作点。

7.1 特殊情形

　　直流分析反映的是输入为直流（即频率(omega=0)）时的状态，需要特殊处理动态元件。

　　电容在直流下的容抗为$ lim limits_{omega rightarrow 0} frac{1}{j omega C} = infty $，显然直流分析时电容应视为两端开路。

　　电感在直流下的感抗为$ lim limits_{omega rightarrow 0} j omega L = 0 $，显然直流分析时应视为两端短路。

　　此外所有作为信号源的电压源视为短路、作为信号源的电流源视为开路。

7.2 直流分析的过程

　　设目标参数(p)，扫描范围([p_{min}, p_{max}])，扫描步长(s)。线性扫描共需要(frac{p_{max}-p_{min}}{s})次方程求解，每次将目标参数设定为(p(n)=p_{min}+ns)，通过改进节点分析（MNA）建立的方程解出对应的节点电压(U(n))。这样(U(n))就形成了直流扫描分析的结果。

　　实用中，有时需要使用对数步进来扫描。

8 交流扫描分析（AC Sweep）

　　AC Sweep分析是正弦稳态电路在频域上的小信号分析。输入变量是正弦频率(omega)，输出变量是电路中各节点电压的频率响应（幅度和相位）。

　　交流分析采用相量法，电压电流都采用相量表示，仍然利用MNA求解，只不过MNA中各矩阵都定义在复数域上。

8.1 电容的相量模型

　　理想电容在正弦稳态电路中的VCR表示为

　　每当一个理想电容加入支路(s rightarrow t)时，只需对MNA的子矩阵的值作如下更新：

8.2 电感的相量模型

　　类似地，理想电感在正弦稳态电路中的VCR表示为

　　每当一个电感加入支路(s rightarrow t)时，只需对MNA的子矩阵的值作如下更新：

8.3 交流分析的过程

　　交流分析非常重要的假设是小信号。在小信号模型中，非线性元件可以在静态工作点处线性化，例如PN结可通过动态电阻(g_d(u))等效。因此在进行交流分析之前，先进行直流分析，确定电路静态工作点。静态工作点确定，式((ref{equ:mna_newtown_format}))中所有雅克比矩阵的值也都确定。这样在交流分析时，不必迭代，而是将其视作线性方程来处理。

9 复频域分析（s域）

　　对电路的微分方程进行Laplace变换可以得到s域上的代数方程，这些代数方程可以用与上一节AC分析相同的方法建立和求解。事实上，上节所述的相量模型可以看作(s = jomega)的特殊情况，这也反映了频域和复频域的关系。

　　s域的MNA混合方程变为：

9.1 Laplace变换

　　给定时域激励信号f(t)，可通过Laplace变换得到复频域上的激励(F(s)=mathscr{L}[f(t)])，将F(s)代入激励源模型中，求解MNA方程即可得到节点电压和分支电流的频域响应(begin{bmatrix} mit{U(s)} & mit{J(s)} end{bmatrix}^{T})。

9.2 Laplace逆变换

　　对于上面得到的频域响应，可通过逆变换得到时域响应(begin{bmatrix}mathscr{L}^{-1}[mit{U(s)}] & mathscr{L}^{-1}[mit{J(s)}]end{bmatrix}^{T})。

10 瞬态分析（时域分析）

　　上节给出了从复频域变换到时域的分析方法，下面直接在时域进行分析，这也是SPICE采用的方法。

　　时域上理想电容和电感的VCR为常微分方程：

　　计算机无法直接处理连续时间系统。可以将时间离散化，然后利用数值方法求解。

10.1 线性多步：隐式GEAR法

　　对于电容或电感特性方程中所出现的形如(f(x,t) = frac{dx}{dt})的常微分方程，可通过积分(x = int f(x,t) dt)来求解。

　　根据黎曼积分的定义，连续时间域上的积分(x = int f(x,t) dt)可通过离散时间域上的累积来近似：

　　其中(h_n=t_{n+1}-t_n)称为第(n)步的步长。

　　将式((ref{equ:num_int}))写成迭代格式：

　　这是一阶显式单步法。单步法的收敛性可参考资料(^{[3]90-92})。为了获得更精确的解，这里采用线性多步法。线性多步法是前(p)步解的线性组合，单步法正是线性多步法的特例。

　　其中(p)是步数。(a_i)、(b_i)是常系数。

　　利用泰勒展开构造线性多步法(^{[5]})，(a_i)、(b_i)应满足：

　　选取一些特殊的(p)、(a_i)、(b_i)值，就能构造出不同的迭代方法。当(b_{-1} ne 0)时为隐式方法，当(b_{-1} = 0)时为显式方法。对于隐式GEAR：

　　给定阶数(k=1,2,cdots)，联立式((ref{equ:gear_pb}))与式((ref{equ:lin_multi_step_ab}))可以解出系数(a_i)、(b_i)。从结果来看，一阶隐式GEAR就是隐式欧拉法（Implicit Euler’s method）。4阶隐式GEAR迭代格式如下：

10.2 线性多步法中的迭代

　　在线性多步法迭代格式((ref{equ:multi_step_format}))中，式子左侧为待求的量(x_{n+1})，而式子右侧也依赖于待求量(x_{n+1})，因此待求量无法直接计算。解决办法是解方程，设方程(f(x_{n+1}) = x_{n+1} – sum_{i=0}^{p}a_i x_{n-i} + h_nsum_{i=-1}^{p}b_i f(x_{n-i},t_{n-i}) = 0)，则只需通过迭代解出该方程的根(x_{n+1})即可。迭代格式为：

　　迭代到(|x_{n+1}^{m+1}-x_{n+1}^{m}|)小于给定误差限时，可以取(x_{n+1}=x_{n+1}^{m+1})。

10.3 预报-校正法

　　从上节可以看出，每步线性迭代中又包含若干(x_{n+1}^{m+1}=g(x_{n+1}^{m}))这样的迭代。初值(x_{n+1}^0)的选取将直接影响到迭代次数，因此初值的选取十分重要。相比于随机给定一个初值，通过预报器预测的初值可能更接近真实值，再进行线性多步迭代时，所需迭代次数将减少。

　　这里采用显式欧拉法实现预报器，预报值(x_{n+1}^{0})计算为

10.4 自适应步长控制算法

　　瞬态分析中，如果时间步长(h_n)选取过大会造成局部截断误差偏大，甚至得出完全错误的结果；而如果步长选取太小则会使得计算量增加，而固定步长在某些区间内往往不是最优，因此一般采用变步长算法。

　　由6.3节可知，(h_n)的选取应使得第(n)步的局部截断误差(xi_{L}^{(n+1)} = |x(t_{n+1}) – x_{n+1}|)满足：

　　其中(xi)是设定的绝对误差限；(xi_r)是设定的相对误差限。一般来说局部截断误差无法精确计算，只能通过Milne公式估计。

　　自适应步长控制中，先设定一个足够小的初始步长(h_0)，每进行一次迭代，就计算出本次迭代的局部截断误差(xi_{L}^{(n+1)})，再通过式((ref{equ:adpt_step}))判定步长的好坏：

• 若(q gt 1)，则说明局部截断误差大于设定的误差限，步长偏大；
• 若(q lt 1)，则说明局部截断误差已经小于设定误差限，若q远小于1则说明步长过小。

　　根据(q)对步长进行动态调整：

　　其中(k)是线性多步法的阶数。

　　假设当前仿真时间为(t_{n+1})，首先利用线性多步法求出解(x_{n+1})，再估计局部截断误差(xi_{L}^{(n+1)})，按上式计算新步长(h’_{n+1})，若(h’_{n+1}，则说明局部截断误差过大，此时仿真时间不向前推进，而是按新步长重新计算当前时间的解(x_{n+1})，重复上述过程；反之则说明局部截断误差已经满足要求，仿真时间可以推进到(t_{n+2})，令(h_{n+2}=h’_{n+1})，结束本次步长调整。

　　下图为瞬态仿真实例：

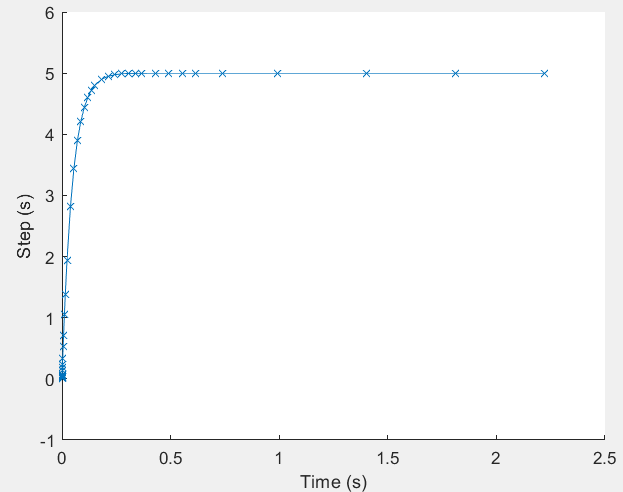
　　图中显示了步长自适应调整，时间轴是均匀的。

10.4.1 断点

　　算法能保证每步迭代局部截断误差的估计值不超出规定的误差限，然而，每次调整步长都要重新计算线性方程组，对于信号快速变化的电路（例如开关电路），步长可能会频繁振荡，从而使仿真器将大量时间花费在寻找合适的步长上。

　　另一个问题出现在维持大步长时（如上图中的平稳部分）突然发生离散事件。在混合数字仿真中，波形存在大量间断点（电平跳变的瞬间）。步长过大会直接越过间断点。需要注意在事件驱动的数字仿真系统中，模拟仿真的误差估计并不会考虑离散事件造成的的跳变，这就是为什么自适应步长控制会失败。

　　因此，涉及数字-模拟混合仿真时，必须使用断点（simulink中称为过零检测）技术，在电平跳变之前插入断点。使模拟仿真器在时间到达断点前，强制减少积分步长，避免错过离散事件。对于模拟仿真，特别是涉及受控开关时，断点同样重要，可有效避免步长振荡。

　　稍微解释一下为什么数字仿真可以预测电平跳变。每个事件从进入队列到被调度执行，需间隔该事件指定的延时，因此事件的执行总是慢于入队。在事件入队时，就可预知断点的位置（入队时间+延迟），从而提前通知SPICE仿真器。

以后有机会可能补充离散-连续系统联合仿真的方法。

10.5 常见储能元件的时域模型

10.5.1 电容的时域模型

　　电容的时域特性描述为：

　　利用线性多步法((ref{equ:multi_step_format}))得到迭代格式：

　　将上式展开并移项（(b_{-1} ne 0)），可得

　　其中：

　　(g_{eq})从物理上可解释为等效电导，(i_{eq})从物理上可解释为等效电流源，于是得到了电容的等效线性化模型，如图4所示。

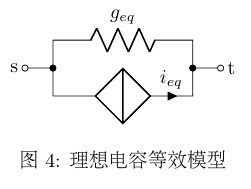
　　根据之前推出的阻抗元件支路对MNA各子矩阵的贡献（式(ref{equ:admit_elem_contrib})）和独立电流源支路对MNA各子矩阵贡献值（式(ref{equ:cs_contrib})）可知对应MNA方程为：

　　因此可知每当一个电容加入支路(s rightarrow t)时，只需对MNA各子矩阵作如下更新：

　　同时应在程序中应设置标记，指出参数({g_{eq}}^{(n)})和({i_{eq}}^{(n)})是需要迭代计算的。给定步长(h_n)，初值(u_0={u_s}^{(0)}-{u_t}^{(0)})，根据上式生成MNA方程，可解出节点电压({u_s}^{(1)})、({u_t}^{(1)})，以此类推。

10.5.2 电感的时域模型

　　电感的时域特性描述为：

　　利用线性多步法((ref{equ:multi_step_format}))得到迭代格式：

　　整理并移项（(b_{-1} ne 0)），可得

　　其中：

　　从物理意义上看，电感可等效为动态电阻(r_{eq})与独立电压源(u_{eq})串联，如图5所示。

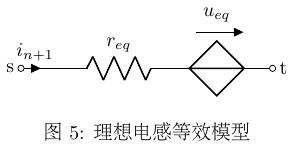
　　根据之前推出的独立电压源的贡献值（式(ref{equ:vs_contrib})）和电流控制电压源支路对MNA各子矩阵贡献值（式(ref{equ:ccvs_contrib})）可知对应MNA方程为：

　　因此每当一个电感加入支路(s rightarrow t)时，只需对MNA各子矩阵作如下更新：

　　同时应在程序中应设置标记，指出参数({r_{eq}}^{(n)})和({u_{eq}}^{(n)})是需要迭代计算的。

10.6 时域分析总流程

• 1 初始化：建立MNA方程。设置当前时间(t=0)，设置积分步(s)、阶数(ord)为初值
• 2 用(s)、(ord)计算GEAR系数
• 3 解MNA方程（流程图见6.2）
• 4 更新时间(t’=t+s)
• 5 检查断点列表，动态调整积分步(s)、阶数(ord)
• 6 判断终止条件，不终止则循环执行 2

11 程序实现

　　详见文章开头给出的github链接。

参考资料

[1] C.W. Ho; Ruehli, A.; Brennan, P. The modified nodal approach to network analysis[J]. IEEE, doi:10.1109/tcs.1975.1084079, 1975: 0–509.

[2] 邱关源. 电路[M]. 第5版, 高等教育出版社, 2006: 391-392.

[3] 李建良等. 计算机数值方法[M]. 东南大学出版社, 2009.

[5] Timothy Sauer. Numerical Analysis[M]. 2nd Edition, George Masonry University, 2011: 336-339.

[6] Thomas L. Quarles. Analysis of performance and convergence issues for circuit simulation[R], University of California, Berkeley Technical Report No. UCB/ERL M89/42, 1989: 30-31.

[7] L. W. Nagel. SPICE2: A Computer Program to Simulate Semiconductor Circuits[R]. University of California, Berkeley Technical Report No. UCB/ERL M520, 1975: 138-142

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.e1idc.net