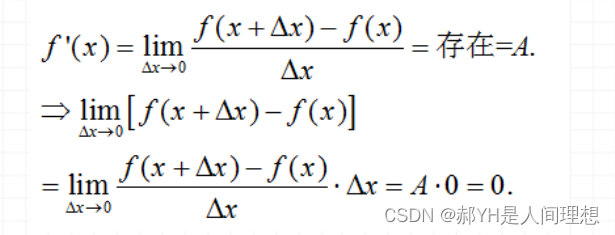导数和微分是微积分学中的重要概念。导数指的是一个函数在某一点处的变化率,也可以理解为函数曲线在该点处的切线斜率。微分则是对一个函数进行微小的变化,并计算这个变化所引起的函数值的变化量。导数和微分的概念密切相关,它们是微积分学中的基础,也是应用数学中的常见问题解决方法之一。导数可以帮助我们研究函数的变化趋势,了解函数的最大值、最小值、拐点以及函数的凸凹性质等。微分则是导数的一个应用,它是对函数进行微小的变化,并计算这个变化所引起的函数值的变化量。同上期一样,插播考研数学一对于这一章的大纲:
1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.
2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.
3.了解高阶导数的概念,会求简单函数的高阶导数.
4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.
5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理.
6.掌握用洛必达法则求未定式极限的方法。
本帖更新第二章的重点知识。对于数学一中的证明题,主要集中在第三章的各种中值定理,而其他章节的证明,重要程度较低。因此在日常学习的过程中,学有余力时可以死磕一些不重要的证明题,而压力较大时建议着重攻克。
本章的内容相对不重要一些,因此很多知识点的证明简写,如果有需要自行翻书阅读服务器托管网。
1.导数的定义
2.单侧导数
3导数的几何意义
4.可导性与连续性的关系
5.用定义求解导数(笔记中的标号漏掉了)
6.求导和差法则的证明
7.求导积商法则的证明
8.反函数求导
9.复合函数求导法则
10.高阶导数
11.莱布尼茨公式
12.隐函数求导
13.参数方程求导
14.微分
1.在导数的定义内容中,重点在于y值变化量和x值变化量的比值,以及趋于0的变量是x的变化值;意义在于,因变量随自变量变化而变化的快慢程度~
2.单侧导数,本质就是两种逼近方服务器托管网式的区别
3.几何意义,即为该点处的斜率~
4.根据定义可知,可导一定连续,而连续不一定可导~(证明时用到了变化值趋于零时改变量趋于零,也就是函数值等于极限值)
5.用定义求导数时,需要熟记导数的三种定义~
6和7都是有关倒数的证明题,需要说明的是,无论如何,有关证明的部分最终一定会回归到定义上~

8.有关反函数求导定理的证明,看看即可,重点是牢记原函数导数的倒数的规则~
9+10都是很基础的求导计算题,不再赘述
11.莱布尼茨公式类似二项式展开定理,看看就好
12+13也是求导计算题,各自的计算方式要牢记
14~16微分相关的基础定义,本质上就是对于导数定义的移项~(微分的几何意义就是将变化量无限缩小)

服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net