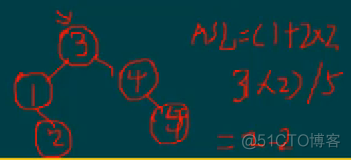文章目录
- 1.构造二叉排序树以及求出查找成功的平均查找长度
- 2.平衡二叉树的定义
1.构造二叉排序树以及求出查找成功的平均查找长度
-
- (1)已知输入序列1,2,3,4,5,请构造二叉排序树,并求出查找成功的平均查找长度
先放节点1,节点2比1大,应该是其右子树,比2大(这个节点是空的),是其右子树,。。节点4比1大,是其右子树,比2大,是其右子树,比3大,是其右子树,比4大(这个节点是空的),
-
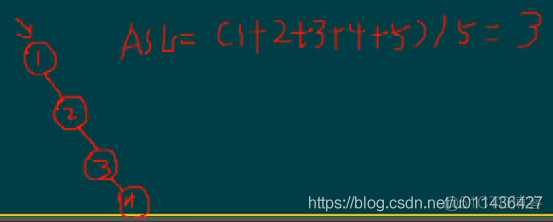
- (2)输入序列3,1,2,4,5,请构造二叉排序树,并求出查找成功的平均查找长度
先放入节点3,节点1比3小,是其左子树,节点2,比3小,是其左子树,比1大,是其右子树,比节点2大(节点是空的),是其右子树。。。。以此类推
2.平衡二叉树的定义
-
- 平衡二叉树或者是一颗空树,或者是具有下列性质的二叉排序数:
(1)它的左、右子树都是平衡二叉树
(2)并且左、右子树的深度之差不超过1
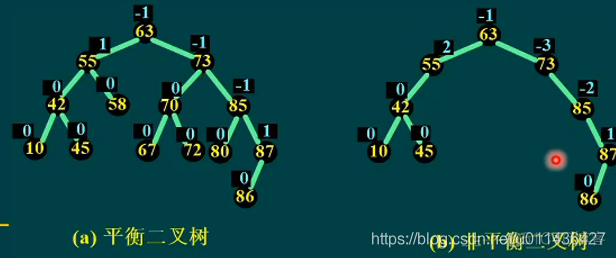
(3)(a)中63节点的深度差计算:4-5=-1
-
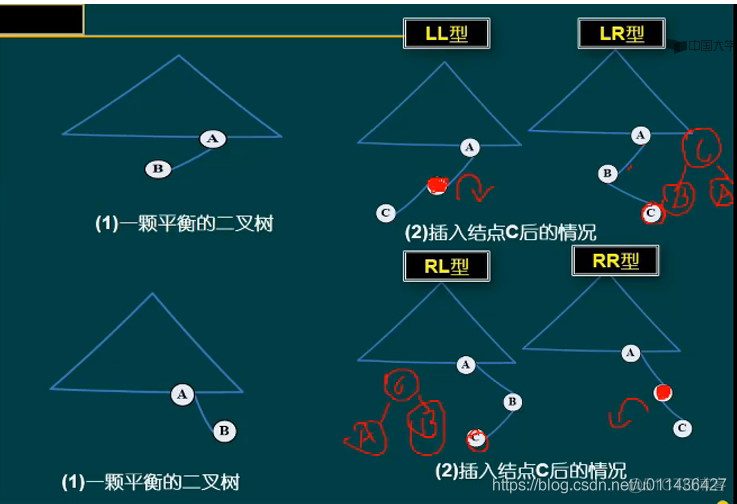
- eg:若一颗平衡二叉树不平衡了,该如何调整?所有的不平衡状态可能有哪些?
每次插入一个节点都要保证他是二叉排序树的定义,所以需要旋转。
下面的LL,LR,RL,RR都是在一颗平衡的二叉树上,增加一个节点而不平衡的。插入后,对于节点A而言,二叉树的高度由1(左子树高度为1,右子树高度为0)->2or-2,,高度值发生了变化,所以需要单旋或者多旋。
(1)LL型和RR型类似:将中间值B右旋成为上面的点,树高由3->2,RR型左旋。
LL型为例,因为中间的比A小,比B大,所以右旋的结果满足二叉排序树的定义,啥都不变。RR型类似
(2)LR型和LL型类似:中间值是c,需要2次旋转
LL型为例,因为节点C比节点A大,比节点B小,所以2次旋转后A为B的左子树,B为A的右子树,旋转过后还是满足二叉排序树的定义!
- 代码
AvlTree Insert(Elementype X, AvlTree T)
{
if (T==NULL)
{
T=malloc(sizeof(struct AvlNode));
if (T==NULL)
FatalError("Out of space!!!");
else
{
T->Element=X;
T->Height=0;
T->left=T->right=NULL;
}
}
else if (XElement)
{
}
else if (X>T->Element)
{
}
T->Height=Max(Heigh(T->Left),Height(T->Right))+1;
return T;
}
=============================================================================
接着else if (XElement),左子树的插入操作
else if(X{
T->Left=Insert(X,T->Left);//成为当前节点的左孩子
if (Height(T->Left) - Height(T->Right) == 2)
{
if (XLeft->Element)//LL型
T=SingleRotateWithLeft(T);
else //LR型
T=doubleRotateWithLeft(T);
}
else if (X>T->Element)//接着else if (X>T->Element),右子树的插入操作
{
T->Right=Insert(X,T->Right);//成为当前节点的右孩子
if (Height(T->Right) - Height(T->Left) == 2)
{
if (X>T->Left->Element)//RR型
T=SingleRotateWithRight(T);
else //RL型
T=doubleRotateWithRight(T);
}
}
================================================
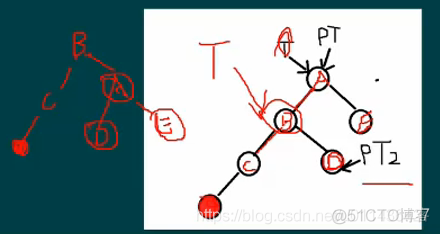
SingleRotateWithLeft的代码如下:
AvlTree SingleRotateWithLeft(AvlTree T)
{
AvlTree pt=T,pT2=T->Left->Right;
T-T->T->Left;//新根
T->Right=pT;
pt->Left=pT2;
return T;
}
//将B作为中间节点,进行旋转
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.e1idc.net