6天通吃树结构—— 第四天伸展树 - 服务器托管|北京服务器租用|机房托管租用|IDC托管租用|机房机柜带宽租用-价格及费用咨询

我们知道AVL树为了保持严格的平衡，所以在数据插入上会呈现过多的旋转，影响了插入和删除的性能，此时AVL的一个变种

伸展树（Splay）就应运而生了，我们知道万事万物都遵循一个“八二原则“，也就是说80%的人只会用到20%的数据，比如说我们

的“QQ输入法”，平常打的字也就那么多，或许还没有20%呢。

一：伸展树

1：思想

伸展树的原理就是这样的一个”八二原则”，比如我要查询树中的“节点7”，如果我们是AVL的思路，每次都查询“节点7”，那么当这

棵树中的节点越来越多的情况下就会呈现下旋，所以复杂度只会递增，伸展树的想法就是在第一次查询时树里面会经过一阵痉挛把

“节点7”顶成“根节点”，操作类似AVL的双旋转，比如下图:

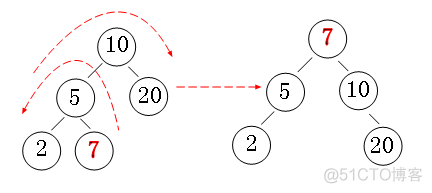
当我们再次查询同样的”数字7“时，直接在根节点处O（1）取出，当然这算是一个最理想的情况，有时痉挛过度，会出现糟糕的”链表“，

也就退化了到O(N)，所以伸展树讲究的是”摊还时间“，意思就是说在”连续的一系列操作中的平均时间“，当然可以保证是log（N）。

2：伸展方式

不知道大家可否记得，在AVL中的旋转要分4个情况，同样伸展树中的伸展需要考虑6种情况，当然不考虑镜像的话也就是3种情况，

从树的伸展方向上来说有“自下而上”和“自上而下”的两种方式，考虑到代码实现简洁，我还是说下后者。

自上而下的伸展

这种伸展方式会把树切成三份，L树，M树，R树，考虑的情况有：单旋转，“一字型”旋转，“之字形”旋转。

①：单旋转

从图中我们可以看到，要将“节点2”插入到根上，需要将接近于“节点2”的数插入到根上，也就是这里的“节点7”，首先树被分成了3份，

初始情况，L和R树是“空节点”，M是整棵树，现在需要我们一步一步拆分，当我们将“节点2”试插入到“节点7”的左孩子时，发现“节点7”

就是父节点，满足“单旋转”情况，然后我们将整棵树放到“R树”中的left节点上，M此时是一个逻辑上的空节点，然后我们将R树追加到

M树中。L树追加到M的左子树中，最后我们将“节点2”插入到根节点上。说这么多有点拗口，伸展树比较难懂，需要大家仔细品味一下。

②：一字型

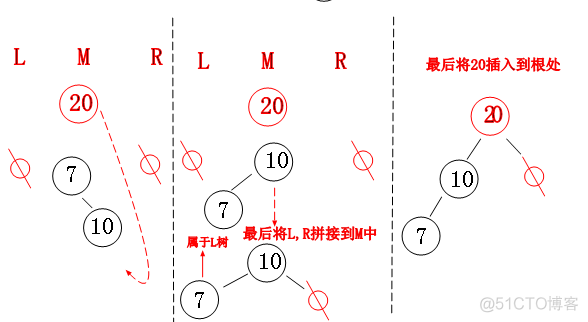
一字型旋转方式与我们AVL中的“单旋转”类似，首先同样我们切成了三份，当我们”预插入20时”，发现20的“父节点”是根的右孩子，

而我们要插入的数字又在父节点的右边，此时满足”一字型“旋转，我们将7，10两个节点按照”右右情况”旋转，旋转后“节点10″的

左孩子放入到L树的right节点，”节点10”作为中间树M，最后将20插入根节点。

③：之字形

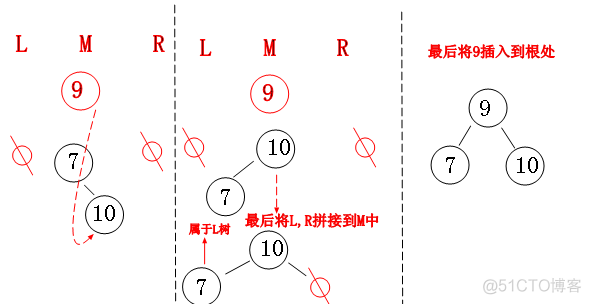
之字形有点类似AVL中的“双旋转”，不过人家采取的策略是不一样的，当我们试插入“节点9”，同样发现“父节点”是根的右儿子，并且

“节点9”要插入到父节点的内侧，根据规则，需要将“父节点10”作为M树中的根节点，“节点7”作为L树中的right节点，然后M拼接L和R，

最后将节点9插入到根上。

3：基本操作

①：节点定义

我们还是采用普通二叉树中的节点定义，也就没有了AVL那么烦人的高度信息。

1     public class BinaryNode
 2     {
 3         // Constructors
 4         public BinaryNode(T theElement) : this(theElement, null, null) { }
 5 
 6         public BinaryNode(T theElement, BinaryNode lt, BinaryNode rt)
 7         {
 8             element = theElement;
 9             left = lt;
10             right = rt;
11         }
12 
13         public T element;
14 
15         public BinaryNode left;
16 
17         public BinaryNode right;
18     }

②：伸展

这里为了编写代码方便，我采用的是逻辑nullNode节点，具体伸展逻辑大家可以看上面的图。

1         #region 伸展
 2         /// 
 3         /// 伸展
 4         /// 
 5         /// 
 6         /// 
 7         /// 
 8         public BinaryNode Splay(T Key, BinaryNode tree)
 9         {
10             BinaryNode leftTreeMax, rightTreeMin;
11 
12             header.left = header.right = nullNode;
13 
14             leftTreeMax = rightTreeMin = header;
15 
16             nullNode.element = Key;
17 
18             while (true)
19             {
20                 int compareResult = Key.CompareTo(tree.element);
21 
22                 if (compareResult  0)
39                 {
40                     //如果成立，说明是”一字型“旋转
41                     if (Key.CompareTo(tree.right.element) > 0)
42                         tree = rotateWithRightChild(tree);
43 
44                     if (tree.right == nullNode)
45                         break;
46 
47                     //动态的将中间树的”当前节点“追加到 L 树中，同时备份在header中
48                     leftTreeMax.right = tree;
49 
50                     leftTreeMax = tree;
51 
52                     tree = tree.right;
53                 }
54                 else
55                 {
56                     break;
57                 }
58             }
59 
60             /* 剥到最后一层，来最后一次切分 */
61             //把中间树的左孩子给“左树”
62             leftTreeMax.right = tree.left;
63 
64             //把中间树的右孩子给“右树”
65             rightTreeMin.left = tree.right;
66 
67             /* 合并操作 */
68             //将头节点的左树作为中间树的左孩子
69             tree.left = header.right;
70 
71             //将头结点的右树作为中间树的右孩子
72             tree.right = header.left;
73 
74             return tree;
75         }
76         #endregion

③：插入

插入操作关键在于我们要找到接近于”要插入点“的节点，然后顶成“根节点”，也就是上面三分图中的最后一分。

1 #region 插入
 2         /// 
 3         /// 插入
 4         /// 
 5         /// 
 6         public void Insert(T Key)
 7         {
 8             if (newNode == null)
 9                 newNode = new BinaryNode(default(T));
10 
11             newNode.element = Key;
12 
13             if (root == nullNode)
14             {
15                 newNode.left = newNode.right = nullNode;
16 
17                 root = newNode;
18             }
19             else
20             {
21                 root = Splay(Key, root);
22 
23                 int compareResult = Key.CompareTo(root.element);
24 
25                 if (compareResult  0)
37                     {
38                         newNode.right = root.right;
39 
40                         newNode.left = root;
41 
42                         root.right = nullNode;
43 
44                         root = newNode;
45                     }
46                     else
47                         return;
48             }
49 
50             newNode = null;
51         }
52         #endregion

④：删除

删除操作也要将节点伸展到根上，然后进行删除，逻辑很简单。

1  #region 删除
 2         /// 
 3         /// 删除
 4         /// 
 5         /// 
 6         public void Remove(T Key)
 7         {
 8             BinaryNode newTree;
 9 
10             //将删除结点顶到根节点
11             root = Splay(Key, root);
12 
13             //不等于说明没有找到
14             if (root.element.CompareTo(Key) != 0)
15                 return;
16 
17             //如果左边为空，则直接用root的右孩子接上去
18             if (root.left == nullNode)
19             {
20                 newTree = root.right;
21             }
22             else
23             {
24                 newTree = root.left;
25 
26                 newTree = Splay(Key, newTree);
27 
28                 newTree.right = root.right;
29             }
30             root = newTree;
31         }
32         #endregion

总的运行代码如下：

1 using System;
  2 using System.Collections.Generic;
  3 using System.Linq;
  4 using System.Text;
  5 
  6 namespace DataStructSplay
  7 {
  8     public class BinaryNode
  9     {
 10         public BinaryNode(T theElement) : this(theElement, null, null) { }
 11 
 12         public BinaryNode(T theElement, BinaryNode lt, BinaryNode rt)
 13         {
 14             element = theElement;
 15             left = lt;
 16             right = rt;
 17         }
 18 
 19         public T element;
 20 
 21         public BinaryNode left;
 22 
 23         public BinaryNode right;
 24     }
 25 
 26     public class SplayTree where T : IComparable
 27     {
 28         public BinaryNode root;
 29 
 30         public BinaryNode nullNode;
 31 
 32         public BinaryNode header = new BinaryNode(default(T));
 33 
 34         public BinaryNode newNode;
 35 
 36         public SplayTree()
 37         {
 38             nullNode = new BinaryNode(default(T));
 39 
 40             nullNode.left = nullNode.right = nullNode;
 41 
 42             root = nullNode;
 43         }
 44 
 45         #region 插入
 46         /// 
 47         /// 插入
 48         /// 
 49         /// 
 50         public void Insert(T Key)
 51         {
 52             if (newNode == null)
 53                 newNode = new BinaryNode(default(T));
 54 
 55             newNode.element = Key;
 56 
 57             if (root == nullNode)
 58             {
 59                 newNode.left = newNode.right = nullNode;
 60 
 61                 root = newNode;
 62             }
 63             else
 64             {
 65                 root = Splay(Key, root);
 66 
 67                 int compareResult = Key.CompareTo(root.element);
 68 
 69                 if (compareResult  0)
 81                     {
 82                         newNode.right = root.right;
 83 
 84                         newNode.left = root;
 85 
 86                         root.right = nullNode;
 87 
 88                         root = newNode;
 89                     }
 90                     else
 91                         return;
 92             }
 93 
 94             newNode = null;
 95         }
 96         #endregion
 97 
 98         #region 是否包含
 99         /// 
100         /// 是否包含
101         /// 
102         /// 
103         /// 
104         public bool Contains(T Key)
105         {
106             if (isEmpty())
107                 return false;
108 
109             root = Splay(Key, root);
110 
111             return root.element.CompareTo(Key) == 0;
112         }
113         #endregion
114 
115         #region 判断是否为空
116         /// 
117         /// 判断是否为空
118         /// 
119         /// 
120         public bool isEmpty()
121         {
122             return root == nullNode;
123         }
124         #endregion
125 
126         #region 伸展
127         /// 
128         /// 伸展
129         /// 
130         /// 
131         /// 
132         /// 
133         public BinaryNode Splay(T Key, BinaryNode tree)
134         {
135             BinaryNode leftTreeMax, rightTreeMin;
136 
137             header.left = header.right = nullNode;
138 
139             leftTreeMax = rightTreeMin = header;
140 
141             nullNode.element = Key;
142 
143             while (true)
144             {
145                 int compareResult = Key.CompareTo(tree.element);
146 
147                 if (compareResult  0)
164                 {
165                     //如果成立，说明是”一字型“旋转
166                     if (Key.CompareTo(tree.right.element) > 0)
167                         tree = rotateWithRightChild(tree);
168 
169                     if (tree.right == nullNode)
170                         break;
171 
172                     //动态的将中间树的”当前节点“追加到 L 树中，同时备份在header中
173                     leftTreeMax.right = tree;
174 
175                     leftTreeMax = tree;
176 
177                     tree = tree.right;
178                 }
179                 else
180                 {
181                     break;
182                 }
183             }
184 
185             /* 剥到最后一层，来最后一次切分 */
186             //把中间树的左孩子给“左树”
187             leftTreeMax.right = tree.left;
188 
189             //把中间树的右孩子给“右树”
190             rightTreeMin.left = tree.right;
191 
192             /* 合并操作 */
193             //将头节点的左树作为中间树的左孩子
194             tree.left = header.right;
195 
196             //将头结点的右树作为中间树的右孩子
197             tree.right = header.left;
198 
199             return tree;
200         }
201         #endregion
202 
203         #region 删除
204         /// 
205         /// 删除
206         /// 
207         /// 
208         public void Remove(T Key)
209         {
210             BinaryNode newTree;
211 
212             //将删除结点顶到根节点
213             root = Splay(Key, root);
214 
215             //不等于说明没有找到
216             if (root.element.CompareTo(Key) != 0)
217                 return;
218 
219             //如果左边为空，则直接用root的右孩子接上去
220             if (root.left == nullNode)
221             {
222                 newTree = root.right;
223             }
224             else
225             {
226                 newTree = root.left;
227 
228                 newTree = Splay(Key, newTree);
229 
230                 newTree.right = root.right;
231             }
232             root = newTree;
233         }
234         #endregion
235 
236         #region 右旋转
237         /// 
238         /// 右旋转
239         /// 
240         /// 
241         /// 
242         public BinaryNode rotateWithRightChild(BinaryNode k1)
243         {
244             BinaryNode k2 = k1.right;
245             k1.right = k2.left;
246             k2.left = k1;
247             return k2;
248         }
249         #endregion
250 
251         #region 左旋转
252         /// 
253         /// 左旋转
254         /// 
255         /// 
256         /// 
257         public BinaryNode rotateWithLeftChild(BinaryNode k2)
258         {
259             BinaryNode k1 = k2.left;
260             k2.left = k1.right;
261             k1.right = k2;
262             return k1;
263         }
264         #endregion
265     }
266 }

伸展树可以总结成一幅图：

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.e1idc.net

服务器托管，北京服务器托管，服务器租用，机房机柜带宽租用