从互联网传输媒体信息在现代已经非常普遍。因此，确保信息传输的安全性非常重要。在现代网络通信中，常用的信息安全技术包括数据加密[1]、数字签名[2]、可信路由策略[3]等。其中，信息加密是保护信息最基本的技术手段。因此，对加密算法的研究显得尤为重要。图像是各种场合广泛使用的信息媒体。

　　但是，图像加密不能以与文本加密完全相同的方式进行。在图像加密中，需要考虑图像的一些固有特性[4]，如数据量大、数据冗余度高、相邻像素之间的相关性高等。由于混沌系统具有对初始条件和控制参数极其敏感、遍历性和类随机行为等良好特性，混沌已成为图像加密的理想工具。因此，基于混沌的图像加密算法成为近年来一个颇具吸引力的研究领域，许多图像加密算法被提出[5]-[12]。

　　在不同的加密方案中，采用了多种策略和不同的混沌系统。 Wu 等人 [13] 利用三维 (3D) 混沌猫图设计了一种高速对称图像加密方案。

　　Wang 等人 [14] 提出了一种使用 3D 混沌贝克图的快速图像加密方案。 Chai [15] 通过使用新的一维 (1D) 混沌映射构建图像加密算法，并模拟粒子的布朗运动来混淆普通图像的位平面。 Huang [16] 利用混沌切比雪夫发生器设计了一种图像加密算法。 Wang 等人 [17] 提出了一种使用交织逻辑映射和 PWLCM 映射的图像加密方案。 Ye [18] 提出了一种基于交织逻辑图的高效对称图像加密算法。 Zhu [19] 提出了一种基于改进超混沌序列的新型图像加密方案，仅通过两轮扩散运算即可实现高密钥灵敏度和高明文灵敏度。 Liu 和 Wang [20] 提出了一种彩色图像加密方案，其中使用分段线性混沌映射（PWLCM）和切比雪夫映射来生成密钥流序列。 PWLCM的系统参数由切比雪夫映射生成的扰动序列修改，PWLCM的初始条件由熵的鼠标位置的MD5哈希值生成。

　　然而，MD5 并不安全，已被教授破解。

　　清华大学王小云。文献[21]提出了一种利用空间位级置换和高维混沌系统的彩色图像加密方案，能够取得良好的加密效果，并能抵抗普通攻击。

　　但是位级排列和高维混沌系统会增加算法的时间开销。文献[22]提出了一种利用DNA互补规则和混沌映射的图像加密方案。将DNA编码原理引入图像加密是一种新颖的方法，但DNA编码也会增加算法的时间开销。在[23]中，提出了一种具有感知器模型的混沌图像加密系统，其中使用神经网络中的高维洛伦兹混沌系统和感知器模型来增强密码系统的安全性。

　　文献[24]提出了一种基于旋转矩阵位级置换和块扩散的图像加密方案，该方案具有适合并行模式和抗噪声攻击的鲁棒性。文献[25]提出了一种利用离散Chirikov标准映射和基于混沌的分数阶随机变换的双重光学图像加密方案，可以实现对光学图像的完全加密。但是分数随机变换增加了计算的复杂度。

　　在[26]中，C.Li等人提出了一种基于混沌帐篷图（CTM）的彩色图像加密方案，该方案只涉及扩散阶段，省略了混淆阶段。因此，纯基于CTM的方案存在一些安全缺陷。最近，Wu 等人[27]提出了一种基于矩形变换和 CTM 的彩色图像加密方案，这是一种增强的基于 CTM 的彩色图像加密方案。 Wu 的方案包括混淆和扩散两个阶段，分别由改进的 2D Arnold 变换和混沌帐篷图控制。这些关于加密方案设计的著作属于密码学的研究范畴，密码学是密码学的一个分支。

　　与密码学相比，密码分析是解密密钥或明文的科学[28]-[30]，是密码学的另一个分支。最近的一些研究表明，一些基于混沌的图像加密算法存在安全漏洞。 Li等人[28]针对叶氏方案[18]开发了纯密文攻击、已知明文攻击和选择明文攻击。 Li 等人 [29] 对 Zhu 的方案 [19] 进行了已知明文攻击。

　　Wang 等人 [30] 利用选择明文攻击破解了 Huang 的算法 [16]。对于其他一些例子，在[31]中提到了几种被破解的基于混沌的图像加密方案。密码分析不仅可以揭示加密算法的弱点，还可以帮助设计者提高加密算法的安全性。如果不找出加密算法中的安全漏洞，那么，将不安全的算法应用到安全通信中，将给通信双方带来严重的安全隐患和损失。因此，密码分析工作对于推动密码学的进步具有重要意义。

　　作为典型的彩色图像加密算法，吴氏加密算法[27]具有结构简单、加密速度快、密码性能好的优点。

　　因此，与传统的图像加密算法相比，它在处理大量数据和减少冗余信息方面具有优势。但吴氏的加密方案也存在一些缺陷。

　　本文对文献[27]提出的加密算法的安全性进行了重新评估，发现存在以下安全问题：（1）不能抵抗选择明文攻击； (2) 加密算法对所有乱码也是不敏感的； (3)解密过程中无法解密密文图像中的第一个像素点； (4) 对矩形逆变换系统的参数选择有额外的限制。针对该安全性缺陷，提出了一种改进的彩色图像加密算法。

　　本文的其余部分安排如下。第二节简要介绍了吴氏算法。详细的密码分析和对 Wu 算法的攻击在第三节中介绍。

　　第四节提出了一种改进的加密方案。

　　第五节给出了改进方案的一些实验结果和分析。最后，第六节给出了结论。

 　　Wu 算法中用于置换像素位置的 2D 矩形变换是改进的 2D Arnold 变换，定义为

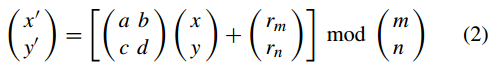
 　　其中 (a, b, c, d) 是变换矩阵的元素，(x, y) 和 (x 0 , y 0 ) 分别是原始图像中像素的位置及其在置换图像中的新位置，而 m 和 n 分别是普通图像的高度和宽度。当满足以下条件时，二维矩形变换具有逆运算，即，

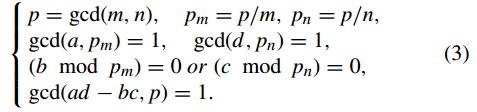
　　 则对式(2)的逆变换表示为

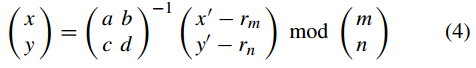
 　　Wu 算法的密钥是混沌帐篷图的 (µ1, µ2, µ3, x10, x20, x30) 和改进的 2D-RT 的 (a, b, c, d, rm, rn, t)。其中(µ1, µ2, µ3)和(x10, x20, x30)分别为CTM系统的控制参数和初始值，t为排列的迭代轮数。

B. WU 的算法

　　为了更清楚地描述吴氏算法，画出该算法的流程图，如图1所示。

　　加密过程包括两个阶段，即排列像素位置和加密像素值。在密码分析中，加密方案就像一个加密机器。图 1 中的虚线矩形框相当于吴氏算法的加密机制。

　　为了更清楚地描述吴氏算法，画出该算法的流程图，如图1所示。

　　加密过程包括两个阶段，即排列像素位置和加密像素值。在密码分析中，加密方案就像一个加密机器。图 1 中的虚线矩形框相当于吴氏算法的加密机制。

　　具体步骤可简述如下：

　　步骤（1）：选择秘钥（a、b、c、d、rm、rn、t）和（μ1、μ2、μ3、x10、x20、x30）。

　　步骤(2)：读取m×n×3大小的彩色明文图像Pm×n×3=[P(i,j,k)]。令 N = m × n，将 Pm×n×3 的三个分量表示为 RPm×n = [RP(i, j)]、GPm×n = [GP(i, j)] 和 BPm×n = [ BP(i, j)]，分别。其中 i = 1, 2, . . . , m, j = 1, 2, . . . , n, k = 1, 2, 3。

　　步骤(3)：将RPm×n、GPm×n和BPm×n三个分量拼接在一起，形成灰度图像PSm×3n = [PS(i, l)]，其中i = 1, 2, . . . , m, l = 1, 2, . . . , 3 名词

　　步骤(4)：将灰度图PSm×3n = [PS(x, y)]利用式(2)进行t轮置换，得到置换后的图像为PRTm×n = [PRT(x 0 , y 0 )]。其中，PRT(x 0 , y 0 ) = PS(x, y)。

　　步骤(5)：将PRTm×3n拆分为三个矩阵RRTm×n、GRTm×n和BRTm×n，大小为m×n。然后将RRTm×n、GRTm×n、BRTm×n进一步转化为三个一维向量RN×1、GN×1、BN×1。其中 N = m × n。

　　步骤（6）：分别以参数（μ1，x10）、（μ2，x20）和（μ3，x30）对式（1）进行N+1000次迭代，取最后的N个值，形成三个混沌序列X1，长度为 N 的 X2、X3。

　　步骤（7）：用 X1，X2，X3 计算三个密钥流 S1，S2，S3

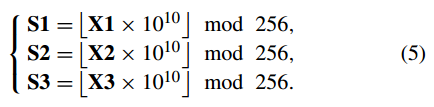
 　　步骤（8）：对RN×1、GN×1、BN×1进行加密，得到它们对应的密文图像R 0 = [R 0 (i)], G0 = [G 0 (i)], B 0 = [ B 0 (i)] 作为

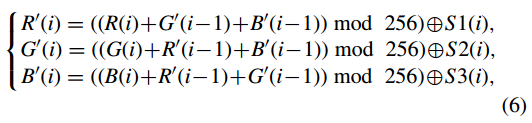
 　　其中 i = 1, 2, . . . ,N.当 i = 1 时，R 0 (i − 1)、G 0 (i − 1) 和 B 0 (i−1) 分别由三个参数 R 0 0 、G 0 0 和 B 0 代替，计算如下：

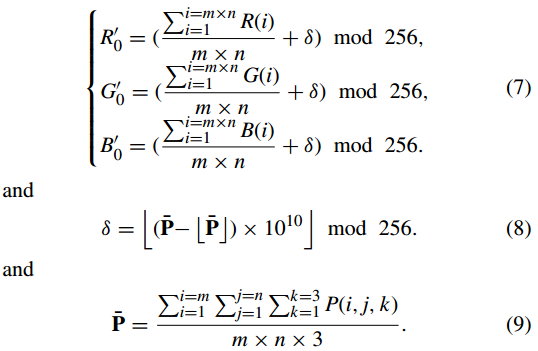
　　步骤(9)：将三个一维向量R 0 、G0 、B 0 整形为三个矩阵RCm×n、GCm×n、BCm×n，并用这三个分量组成最终的彩色密码图像C。

　　解密算法是加密算法的逆运算。这里将解密算法的两个关键操作步骤简述如下。

　　首先，在反向扩散过程中，从 R 0 、G0 和 B 0 中回收 R、G 和 B 的公式为

　　其中 i = 1, 2, . . . ,N.当i = 1时，R 0 (i − 1)、G 0 (i − 1)和B 0 (i − 1)分别被三个参数R 0 0 、G 0 0 和B 0 0 代替。值得注意的是，R(1)、G(1)和B(1)的第一个像素值无法被解密，因为R 0 0 、G 0 0 和B 0 0 的值是未知的。这些值需要通过普通图像的像素值来计算。

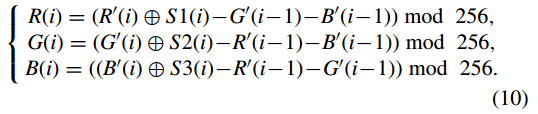
 　　其次，在反向混淆过程中，从置换灰度图像PRTm×3n恢复未置换灰度图像PSm×3n的公式为式(4)。结果，必须满足由公式(3)表示的条件。

C. 原算法的主要缺陷

　　吴氏算法存在四个主要缺陷，归纳如下：

　　（1）吴氏算法使用的密钥与要加密的明文图像无关，因此吴氏算法不能抵抗选择明文攻击。

　　(2) 当任何一个参数(µ1, µ2, µ3, x10, x20, x30)发生变化时，它只会改变其中一个序列(S1, S2, S3)。结果，Wu 的算法对所有密钥都不敏感。

　　(3) 解密过程中，R 0 0 、G 0 0 、B 0 0 未知，无法计算。结果，无法解密第一个像素。

　　(4) 在反向混淆过程中，Wu 等人。阿尔。采用逆二维阿诺德变换，要求参数（a，b，c，d）满足式（3）表示的限制条件。

　　根据 Kerchoff 原理 [32]，在分析加密算法时，假设密码分析者确切地知道密码系统的设计和工作，除了密钥。即攻击者知道密码系统的所有工作机制，但不知道密钥。经典的攻击类型有四种：

　　 (1) 仅密文攻击：对手只拥有目标密文。

　　(2) 已知明文攻击：对手拥有一串明文，以及对应的密文。

　　(3) 选择明文攻击：对手获得了对加密机制的临时访问权。因此，他或她可以选择任何明文，并获得相应的密文。

　　(4) 选择密文攻击：对手获得了对解密机器的临时访问权。因此，他或她可以选择任何密文，并获得相应的明文。

　　选择一个全零元素组成的明文图像U，通过加密机制得到其对应的密文图像V。 U的置换图像对应的一维向量是R、G和B。V对应的一维向量是R 0 、G0和B 0 。由于置换过程没有改变明文图像的像素值，因此R、G、B中的像素值都为零。

　　相应地，R 0 0 、G 0 0 和B 0 0 的值可以由式（7）得到，R 0 0 = 0，G 0 0 = 0，B 0 0 = 0。根据式（6） , 然后可以恢复密钥流 S1, S2 和 S3 为

　　其中 i = 1, 2, . . . ,N, 在 i = 1 的情况下，R 0 (0) = R 0 0 = 0，G 0 (0) = G 0 0 = 0，B 0 (0) = B 0 0 = 0。

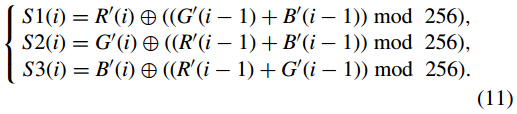
 B. 恢复位置遍历矩阵

　　一幅大小为 m×n×3 的彩色图像有（3mn）个像素点，每个像素点的值是 1 到 255 之间的整数。

　　如果(3mn)≤255，则只需要一张选择明文图像来恢复位置遍历矩阵T，使得选择明文图像中的每个像素在集合{1, 2, . . . , 255}。如果(3mn)>255，则恢复位置遍历矩阵T所需的选择明文图像的数量为d3mn/255e，因此任意选择的图像有255个像素点，取值范围为1~255，其余像素点有同值零。

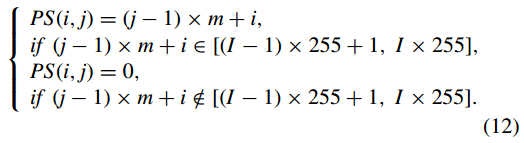
 　　其中PS为U对应的m×3n灰度图像，I = 1, 2, . . . , d3mn/255e。利用第I个选择的明文图像及其对应的密文图像以及前面得到的密钥流S1、S2和S3，我们可以恢复出第I个置换图像PRT。然后我们可以通过比较第 I 个选择的明文图像矩阵 PS 和它对应的置换灰度图像矩阵 PRT 来恢复矩阵 T 中最多 255 个元素的值。使用d3mn/255e选择明文图像及其对应的密文图像，可以解决T中的所有（3mn）个元素。

　　在 A 子节中，我们得到了混沌密钥流 S1、S2 和 S3，它们只与密钥（µ1、µ2、µ3、x10、x20、x30）相关，与明文图像无关。

　　在子Section B中，我们还得到了整个置换矩阵T，它只与秘钥(a, b, c, d, rm, rn, t)有关。因此，我们可以破解由具有相同参数（μ1、μ2、μ3、x10、x20、x30；a、b、c、d、rm、rn、t）的相同加密机制加密的任何其他密文图像 C。

　　从 C 中恢复 P 的解密过程如下：

　　步骤(1)：将彩色密码图像C整形为一维向量R 0 、G0和B 0 的三个分量。

　　步骤(2)：对于 i = 1, 2, . . . ,N,利用式(10)恢复一维向量R、G、B中除R(1)、G(1)、B(1)之外的三个分量。由于R 0 0 、G 0 0 和B 0 0 的值未知，因此R(1)、G(1)和B(1)无法恢复。为简单起见，我们设 R(1) = R 0 (1)、G(1) = G 0 (1)、B(1) = B 0 (1)。

　　步骤(3)：将大小为(m×n)×1的一维向量R、G、B的三个分量合并为大小为m×3n的灰度图像矩阵PRT。

　　步骤(4)：对PRT中的每个像素位置(x,y)，利用T进行逆置换运算得到PS如下：

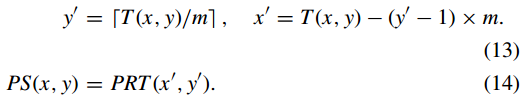
　　步骤(5)：将m×3n大小的矩阵PSm×3n拆分为三个m×n大小的矩阵，即RPm×n、GPm×n、BPm×n。

　　步骤(6)：将RPm×n、GPm×n和BPm×n三个分量组合起来，得到最终的解密彩色图像P。

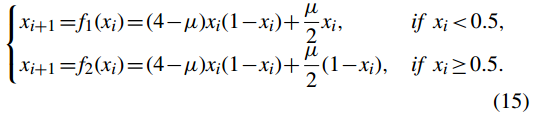
　　命题 1：如果 µ ∈ (0, 4) 且 xi ∈ (0, 1)，则系统 (15) 是一个映射 f：xi ∈(0, 1)→ xi+1 ∈ (0, 1)。

　　证明函数 f1(x) 可以转换为标准二次函数形式：f1(x) = (µ − 4)x 2 + (4 − µ/2)x。

　　对于 µ 1/2。因此，当 x 0) > f1(x = 0) = 0。

　　为了比较新系统和帐篷地图系统的混沌特性，分别使用分岔图和李亚普诺夫指数图描述了两个系统的混沌动力学行为。无花果。图3(a)和3(b)分别是帐篷图的分岔图和李雅普诺夫指数图。

无花果。图3(c)和3(d)分别是LTM的分岔图和Lyapunov指数图。从图 3 可以看出，当 µ 在 (1, 2] 范围内时，帐篷图具有正李雅普诺夫指数，处于混沌状态，且范围很小。此外，混沌序列的状态值分布{xi} 在 [0, 1] 范围内很不均匀。

然而，新的LTM系统具有正的Lyapunov指数，当μ在(0, 4)范围内时处于混沌状态，μ值的范围远大于帐篷图。此外，所提出的新 LTM 系统的状态值 {xi} 的分布在 [0, 1] 范围内更加均匀。

　　如果所有的 P 值 > α，则该序列被认为是随机的。我们使用 LTM 生成三个序列并将它们转换为三个长度为 1000000 的二进制序列，使用 NISTSP800-22 套件测试了 15 个指标，这些序列的最小 P 值列在表 1 中。从表 1 中，我们可以看到最小P值结果大于显着性水平α，说明检验满足SP800-22随机性要求。

　　因此，LTM 系统产生的随机数适合加密。

步骤 (1)：选择密钥 {a, b, c, d, rm, rn, t, µ1, µ2, µ3, x10, x20, x30}。

步骤(2)：读取m×n×3大小的彩色明文图像Pm×n×3 = [P(i, j, k)] (i = 1, 2, . . . , m, j = 1, 2 , . . . , n, k = 1, 2, 3)，将3D矩阵Pm×n×3转化为2D矩阵得到灰度图PSm×3n = [PS(i, l)]，其中i = 1, 2, . . . , m, l = 1, 2, . . . , 3 × n。操作方法同吴氏加密算法的步骤（2）和（3）。

步骤(3)：使用SHA-3哈希算法生成一个256bit的明文图像哈希值H，可分为32个8bit大小相同的块。即，H = h1h2。 . . h32, hi ∈ [0, 255], i = 1, 2, . . . , 32. 利用哈希值H计算参数δ为

δ也被用作密钥。

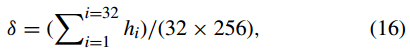
 步骤（4）：修改初始值（x10，x20，x30）为 因此，更新后的参数（x10，x20，x30）与明文图像Pm×n×3的内容有关。

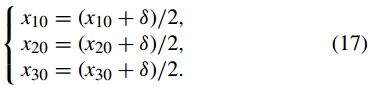
步骤(5)：对灰度图像PSm×3n进行置换，得到置换后的图像PRTm×3n。具体操作方法如下： 对PSm×3n中任意一个像素点的位置(x,y)，将式(2)迭代t次，得到该像素点在PRTm中的位置(x 0 ,y 0 ) ×3n。因此，我们得到 PRT(x 0 , y 0 ) 作为 PRT(x 0 , y 0 ) = PS(x, y)。对所有位置的像素点进行处理后，得到置换图像PRTm×3n。

然后将PRTm×3n拆分为三个矩阵RRTm×n、GRTm×n、BRTm×n，大小为m×n。进一步，将 RRTm×n、GRTm×n 和 BRTm×n 转换为三个一维向量 RN×1、GN×1 和 BN×1，大小为 N × 1。其中 N = m × n。

步骤(6)：计算三个参数R 0 0 、G 0 0 和B 0 0 为

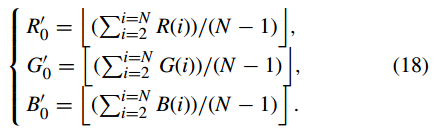
步骤(7)：分别以参数{μ1，μ2，μ3}和修正值{x10，x20，x30}迭代新混沌系统方程(15)N+1000次，取最终的N个值形成三个长度为 N 的混沌序列 X1、X2、X3。

步骤(8)：通过式(5)计算三个密钥流S1、S2、S3和X1、X2、X3。

步骤(9)：将密钥流S1、S2、S3修改为

 步骤(10)：对每个像素加密三个分量{R(i), G(i), B(i)}，得到它们对应的密码值{R 0 (i), G 0 (i), B 0 ( i)} as 当i = 1时，R 0 (i − 1)、G 0 (i − 1)和B 0 (i − 1)分别被三个参数R 0 0 、G 0 0 和B 0 0 代替，这是由等式计算的。 (18).通过使用等式。 (20)，我们使密文和明文的关系更加复杂。

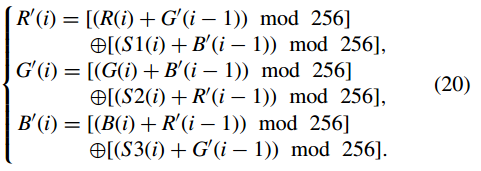
 步骤(11)：重构三个一维向量 R 0 N×1 = [R 0 (i)]，G0 N×1 = [G 0 (i)]，B 0 N×1 = [B 0 (i)]到三个矩阵RCm×n，GCm×n，BCm×n，用这三个分量组成最终的彩色密码图像Cm×n×3。

解密过程与加密过程类似，只是运算顺序相反。

步骤（1）：接收秘钥，即参数集{a, b, c, d, rm, rn, t, µ1, µ2, µ3, x10, x20, x30, δ}。

步骤(2)：接收彩色密码图像Cm×n×3，将三维矩阵Cm×n×3分解为三个二维分量矩阵，分别记为RCm×n、GCm×n、BCm×n。

步骤（3）：利用方程（17）用δ修改初始参数{x10，x20，x30}。

步骤（4）：分别用修改后的初始值{x10，x20，x30}和系统参数{μ1，μ2，μ3}迭代新的混沌系统方程（15）N+1000次，取最终的N个值形成三个长度为N的混沌序列X1，X2，X3。

步骤(5)：利用式(5)分别用X1、X2、X3计算三个密钥流S1、S2、S3，并分别利用式(19)修改S1、S2、S3。

步骤(6)：将三个二维矩阵RCm×n、GCm×n、BCm×n分别整形为三个一维向量R 0 mn×1 、G 0 mn×1 、B 0 mn×1 。

步骤(7)：将R 0 mn×1 , G 0 mn×1 , B 0 mn×1 反向扩散得到部分三个解密向量Rmn×1, Gmn×1, Bmn×1 为

其中 i = N,N − 1, . . . , 2.

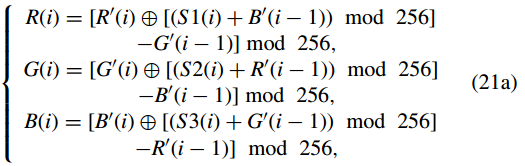
 步骤 (8)：因为现在 {R(2), R(3), . . . , R(N)}, {G(2), G(3), . . . , G(N)}, 和 {B(2), B(3), . . . , B(N)} 是已知的，因此，我们可以利用式（18）计算出（R 0 0 , G 0 0 , B 0 0 ）的值。

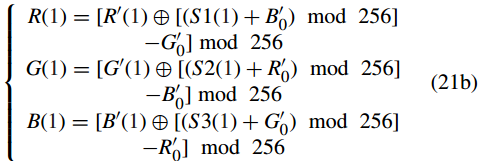
步骤(10)：将Rmn×1、Gmn×1、Bmn×1整形为三个矩阵RRTm×n、GRTm×n、BRTm×n，然后拼接成灰度图像PRTm×3n。

步骤(11)：对灰度图像PRTm×3n进行逆置换得到未置换灰度图像PSm×3n。与Wu的方法不同，这里我们仍然使用改进的2D Arnold变换方程（2）代替逆变换方程（4）。具体操作方法如下： 对PSm×3n中任意一个像素位置(x,y)，将式(2)迭代t次，得到该像素在PRTm×中的位置(x 0 ,y0 ) 3n.因此，我们得到 PS(x, y) 作为 PS(x, y) = PRT(x 0 , y 0 )。对所有位置的像素点进行处理后，得到未经置换的灰度图像PSm×3n。

步骤(12)：将PSm×3n拆分为三个矩阵，即RPm×n、GPm×n、BPm×n。

步骤(13)：最后，解密后的彩色图像Pm×n×3可以由其三个分量RPm×n、GPm×n、BPm×n组成。

D. 改进方案的理论分析

根据处理原理，改进后的方案可以克服吴氏方案的以下不足。

1）新的组合混沌系统，Logistic-tent map（LTM），混沌性能优于tent map。

2) 通过引入与明文图像的SHA-3哈希值相关的参数作为密钥，将密钥流与待加密图像相关联，使改进算法能够抵抗选择明文攻击。

3)通过改进参数R 0 0 、G 0 0 、B 0 0 的生成方法，解密端可以准确计算出这些参数，从而实现对图像的完整解密。

4) 通过改进生成密钥流S1、S2、S3的方法，使改进后的算法对(µ1、µ2、µ3、x10、x20、x30)中的每个初始密钥更加敏感。

5) 通过改进扩散过程中的加密公式，使密文与明文的关系更加复杂。

 　　在模拟实验中，我们通过等式计算了 Lena 纯图像（大小为 512×512）及其加密图像的直方图的方差。 (22).三种不同加密算法加密后的Lena明文图像及其对应的密文图像的直方图方差如表2所示。从结果可以看出，我们的算法得到的密文图像Lena的方差最小，即 3485.1953，远小于 Zhang 的算法 [33] 和 Zhu 的算法 [34]。因此，我们改进的彩色图像加密算法更加高效和安全。

　　香农熵 [35] 通常用于衡量图像灰度值的随机性。对于 8 位图像，香农熵定义为 其中 mi 表示第 i 个灰度值，而 P(mi) 是值 mi 存在于图像中的概率。显然，对于一个8位完全随机的图像，P(mi) = 1/256，熵为8。一个好的加密算法应该使密文图像的香农熵非常接近8。

　　对于大小为 m×n×3 的彩色图像，我们将其转换为大小为 m×3n 的灰度图像来计算香农熵。

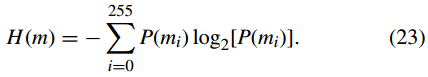
 　　不同相关算法加密的不同密文图像的结果如表4所示。注意，我们的改进算法在大多数情况下获得最高的熵，这意味着我们的改进算法在三个算法中泄漏的信息最少。

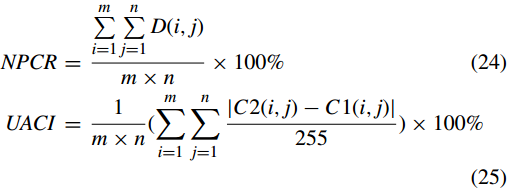
 其中m、n分别表示图像中像素的总行数和列数。 C1(i, j)和C2(i, j)是上述两张加密图像在相同位置(i, j)的像素值，D(i, j)计算为

NPCR的理想值接近1，UACI的理想值接近0.3346[38]。 NPCR 和 UACI 的值越大，说明算法抗差分攻击的性能越好。

　　在我们的改进方案中，密钥流（S1、S2、S3）与要加密的明文图像相关。即使攻击者用一些特殊选择的明文图像破解了密钥流（S1，S2，S3），密钥流（S1，S2，S3）也不能用于解密目标密文图像，因为不同的图像具有不同的密钥-流（S1、S2、S3）。

　　进一步地，在扩散过程中，加密值不仅与对应的明文值和密钥有关，还与原明文值和原加密值有关。这意味着不同的加密图像具有不同的原明文值和原加密值。因此，改进后的算法可以抵抗选择的明文/密文攻击，并且可以很好地抵抗四种经典类型的攻击。

　　本文分析了一种彩色图像加密算法，并利用选择明文攻击对其进行了破解。此外，我们还提出了一种改进的彩色图像加密算法。改进后的算法包括以下三个主要改进。

　　首先，提出了一种新的组合混沌系统，称为Logistic-tent map (LTM)，它具有比tent map更好的混沌性能。

　　其次，将新的混沌系统应用到改进的加密方案中。

　　第三，通过改进密钥生成方法和加密策略，新的加密方案可以克服原加密方案的安全缺陷。分析和实验结果表明，改进后的算法能够显着提高加密图像的安全性，同时仍然具有吴氏算法的所有优点，具有更好的应用潜力。本文提出的改进图像加密算法适用于对安全性要求较高的彩色图像的加密，也适用于灰度图像的加密。