来学点好玩的。
引入
我们也许学过,(FFT) 可以解决一类卷积:
]
现在我们稍微变一下式子:
]
]
]
上面那个圆圆的东西是异或
怎么求?
(FWT) 或
也就是这个式子:
]
(FWT) 的定义
模仿 (FFT),对于 (A) 我们想要在可接受时间内得到一个 (FWT(A)),使得
]
(i) 代表第 (i) 个位置的数。
这样我们就可以 (O(n)) 暴力乘起来了。
因此我们构造 (FWT(A)_i=sum^{}_{j|i=i}A_j)。
现在我们来证明这个构造的正确性。
]
]
]
因为可以从 (j|i=i) 与 (k|i=i) 中得出 ((j|k)|i=i),所以我们还可以消去另一个式子
]
根据 (FWT) 的定义,这个式子就是 (FWT(C)_i)。证毕。
另一种理解
涉及到了或运算,我们不妨把数全都变成二进制。于是我们想到一种经典转换:将二进制中的 (0) 与 (1) 转化为集合中一个数选还是不选。那么或操作代表什么呢?
bingo!两个集合的并集!
于是我们可以把上面的式子改写一个形式:
]
变成
]
注意看,这时 (i,j,k) 都是集合,只不过我们将其用二进制表示.
这样我们可以改写 (FWT) 的定义。
重新来一遍,(FWT(A)_i=sum^{}_{k subseteq i} A_k)。
因此我们为 (FWT) 找到了新的定义,他代表着集合 (i) 的子集之和。我们有了更自然的推导:
]
]
]
]
]
换句话说,我们对子集做了个前缀和操作(发现了吗?子集的前缀和进行或卷积与普通前缀和进行加法卷积具有相似性),并用前缀和相乘代替了原来的 (O(n^2)) 相乘。
如何变化
我们把原序列 (A) 按下标最高位是 (0) 还是 (1) 分成两部分 (A_0) 与 (A_1) 分治求解。显然,前半部分(最高位为 (0) 的部分)就是 (FWT(A_0)),所以我们考虑后半部分的答案。
后半部分最高位为 (1),因此此时“子集”这一概念不仅包含分治处理的他子集,还包括把最大值变为 (0) 后的,序列 (A0) 中同一位置的子集。要将 (A_0) 中的同一位置加到当前答案上。
写成数学形式就是:
]
上面的 (merge) 代表拼接,就是字面意思。
于是我们就能写出分治递归代码了!但为了常数着想,我们试着把递归这一步骤去掉。
去掉的部分并不难写,我们按照层数从小到大递归,不难发现第 (i) 层(从 (0) 开始编号,最底层为 (0))就是枚举第 (i) 位是 (0) 还是 (1),并且乱填其他数进行转移。
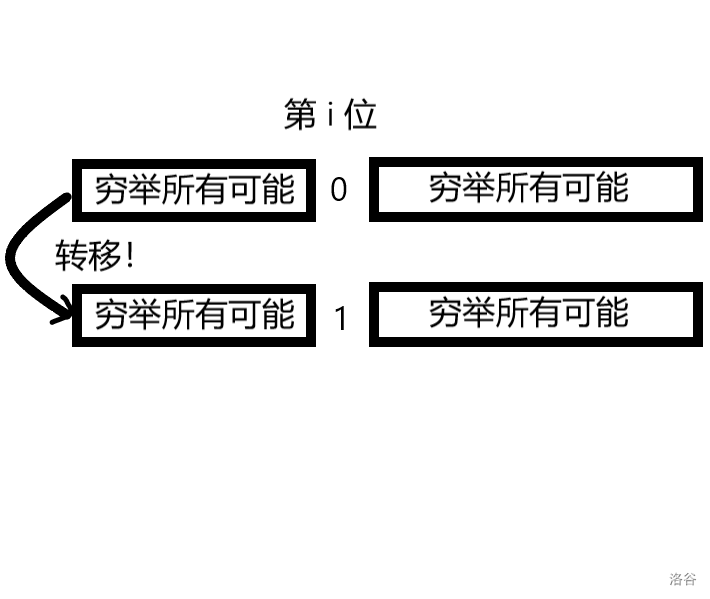
代码也简单:
void OR(mint *f){
for(int o = 2, k = 1; o 如何转回来
再看一眼转移的式子
]
思考只有两个数的情况。此时 (1) 位置是不会变的,(2) 位置加上了 (1) 位置的贡献,要减去。
我们发现更大的情况也是一样的,只要依次把前面的贡献减去就好。
void IOR(mint *f){
for(int o = 2, k = 1; o 这两份代码显然是可以合并的。因此我们得到了 (FWT) 或 的全过程。
void OR(mint *f, int type){
for(int o = 2, k = 1; o (FWT) 与
和 或 差不多,只是要从 (1) 转移到 (0)。
可以发现,实际上我们用子集后缀和优化了运算。
void AND(mint *f, int type){
for(int o = 2, k = 1; o (FWT) 异或
]
很遗憾,我并没有发现这个东西的集合意义,如果有大佬知道可以告诉我。。。
正着转化
思考 (FWT) 的作用,我们想要把 (A_kB_j) 变成 (A_iB_i) 的形式,以此来简化运算。
我们考虑这样 (n) 个 (n) 维向量 (b),(b(i)) 只有下标 (i) 处是 (1),其他位置都是 (0)。
现在我们把 (FWT) 后的 (A,B) 看作系数,此时显然 (A_1b(1),A_2b(2),…,A_nb(n)=A_1,A_2,A_3,A_4…,A_n)
显然,异或卷积对于乘法有分配律。
设异或卷积为 (ast),则
]
]
发现后面的东西可以简单表示,即 (b_i ast b_i = b_i,b_i ast b_j = 0(i neq j))。
那么整个式子就是我们寻找的形式:
]
而我们要做的事情无非是求出 (FWT) 之前的 (b_i)。
太长不看版:异或 (FWT) 与原序列线性相关
既然这样,我们设 (FWT(A)_x=sum^{n}_{i=1} g(x,i)A_i)。
那么因为 (FWT(C)_x=FWT(A)_xtimes FWT(b)_x)
所以 (sum^{n}_{k=1} g(x,k)C_k=sum^{n}_{i=1} g(x,i)A_i times sum^{n}_{j=1} g(x,j)B_j)。
整理一下可以得出:
]
把 (C_k) 用 (A,B) 表示可得:
]
更改求和顺序,我们枚举 (i,j) 可得:
]
于是我们发现了 (g) 的关系:
]
现在问题来了,与 (i,j) 相关的什么东西,使异或之后的值等于原来两值的乘积?
于是我们可以想到有人托梦给我奇偶性。
具体的,我们发现异或前后 (1) 的个数奇偶性不变。原因如下:
按每一位依次考虑。如果第 (i) 位异或后为 (1),那么原来必定有且仅有一个 (1)。个数不变
如果为 (0),要么是两个 (0),此时 (1) 的个数不变,要么是两个 (1),此时 (1) 的个数减 (2),奇偶性仍不变。
所以我们定义 (g(x,i)=(-1)^{|i bigcap x|})。那么上式就等价于:
]
根据上面的推论,左右两边奇偶性不变,与 后无非是减去两个相同的数,奇偶性还是不变。
于是我们得出 (FWT) 的转移式:
]
如何求解
考虑模仿前两个 (FWT) 的形式,讨论最高位 (i) 为 (0) 和为 (1) 两种情况。
原来最高位为 (0),(FWT) 后的前 (2^{i-1}) 个数最高位还是 (0)。由于 (1 And 0=0),所以后 (2^{i-1}) 个数的贡献为正。前半部分答案为 (FWT(A_0)+FWT(A_1))。
(FWT) 后的后 (2^{i-1}) 个数最高位变成了 (1),此时 (A_0) 的贡献还是正(因为 (1 And 0=0))。但是此时后半部分加了 (1),于是贡献要取反。后半部分答案为 (FWT(A_0)-FWT(A_1))。
所以我们得出:
]
当然,参照 或 FWT,我们可以写出不依赖递归的程序:
void XOR(mint *f){
for(int o = 2, k = 1; o 求逆变换
实际上就是把贡献减去
]
显然这两个东西是可以合并的。于是我们可以得出模板的完整代码:
#include
using namespace std;
#define forp(i, a, b) for(int i = (a);i = (b);i --)
const int maxn = 6e5 + 5;
const int mod = 998244353;
int read(){
int u;cin >> u;return u;
}
class mint{
private : int v;
public:
mint(){}
int operator()(void)const{
return v;
}
mint (const int &u){
v = u % mod;
}
mint operator+(const mint &a) const{
int x = a.v + v;
if(x >= mod) return mint(x - mod);
if(x >= 1;
}
return ans;
}
mint inv2 = qpow(2, mod - 2);
int n;
mint A[maxn], B[maxn], C[maxn];
mint g[maxn];
void OR(mint *f, int type){
for(int o = 2, k = 1; o 大概就是这样。。。应用也许会另外开坑吧。
后记
感谢 xht 的博客,从这篇博客里我学到了 FWT 的基础知识。
感谢同校大佬 yllcm 为本人解释符号与定义。
感谢万能的U群群友 Untitled_unrevised 解释 FWT 的目的。
感谢万能的U群群友 rqy 学姐与 樱初音斗橡皮 解释为什么异或 FWT 是线性变换顺便发现了我在线性代数方面的巨大缺口
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.e1idc.net

