在学习了一些games101的课程之后,我还是有点困惑,对于计算机图形学的基础知识,总感觉还是缺乏一些更加全面的认识,幸而最*在做games101的第五次作业时,查询资料找到了scratchpixel这个网站,看了一些文章,终于把脑子里的一团乱麻组织起来了,也就有了这篇关于图形学的第一篇博客。
想要更好的理解这篇博客,强烈推荐先学习games101中关于transformation,rasterization和ray tracing的第一部分
以下内容参考:https://www.scratchapixel.com/lessons/3d-basic-rendering/computing-pixel-coordinates-of-3d-point/perspective-projection.html
https://www.scratchapixel.com/lessons/3d-basic-rendering/computing-pixel-coordinates-of-3d-point/mathematics-computing-2d-coordinates-of-3d-points.html
https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-generating-camera-rays/generating-camera-rays.html
如果内容有误,欢迎指出
-
光栅化与光线追踪中的空间变换
- 光栅化与光线追踪的理解
- 不同空间的介绍
- 光栅化中的空间变换
- 光线追踪中的空间变换
光栅化与光线追踪的理解
在图形学中一个很重要的问题就是,我们如何把一个三维空间中的物体,去展示到一个二维*面上。
这件事其实我们可以分成两步去做,第一步是解决visibility的问题,第二步是解决shading的问题。
怎么理解这两种方法呢?我们先想象,现在在一个无穷大的场景里面,有很多物体,还有一个摄像机,摄像机面前一定距离有个*面,现在我们想知道通过摄像机在它面前这个二维*面上看到的所有三维物体的形象。
光栅化方法,就是把场景内的所有物体先都投影到这个*面上,然后进行着色shading,这里就是光栅化比较麻烦的地方,我们需要设计着色模型(games101中的bling-phone模型),考虑到物体的空间先后顺序我们需要z-buffer,考虑到阴影效果我们需要shadow map,以及纹理贴图来帮助我们。
而光线追踪,模拟了光线在场景中的传播,在光线追踪中,从观察点(或相机)出发的光线被跟踪以确定它们与场景中的物体相交点,然后计算反射、透射和光照等效果,是一种基于物理的渲染方法。
通过上述描述,我们可以发现光栅化可以短时间内处理大量物体,但在光照效果等方面不如光线追踪,而光线追踪速度较慢,因为需要考虑到光线的种种复杂的传播情况,这也就导致光栅化主要用于实时渲染,而光线追踪主要用于离线渲染
我们再来考虑针对这两种方法的空间变换,我们会发现这两种方法其实在干相反的事情,光栅化的坐标变换是把三维变二维,光线追踪是需要摄像机到*面上每个像素点连接的光线,然后求光线与物体的交点,实际上需要我们把二维的点转换为三维,具体的过程我们在接下来的部分阐述
不同空间的介绍
要理解光栅化与光线追踪的空间变换,我们首先要搞清楚几个空间的定义
世界空间:世界空间就是我们之前提到的无穷大的场景,所有的点的定义最初都是在这个三维空间中,与之对应的是世界坐标系
相机空间:相机空间就是以相机为坐标原点的坐标系建立的空间,我们可以使用games101中提到的camera transformation对应的矩阵,实现世界坐标系到相机坐标系之间的转换,一般来说,我们的相机的位置在(0,0,0)这个坐标原点,朝向世界坐标系的-z方向。
屏幕空间:屏幕空间是一个二维空间,相机空间中的点经过透视变换可以到image plane上,然后我们根据画布(canvas)的范围,可以在image plane这个无穷大的*面上划分出屏幕空间
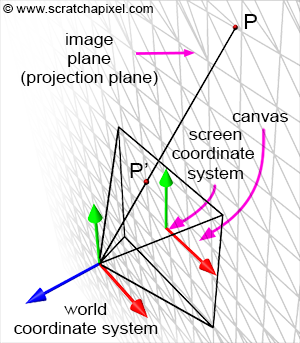
NDC空间:把屏幕空间坐标系标准化到【0-1】的空间中
栅格空间:NDC空间中的2D点被转换为2D像素坐标,为此,我们将标准化点的 x 和 y 坐标乘以像素宽度和高度,从 NDC 到栅格空间还需要反转该点的 y 坐标。 由于像素坐标是整数,因此最终坐标需要四舍五入到最接*的以下整数。
下面的图很形象地展示了上面的三个空间的区别:
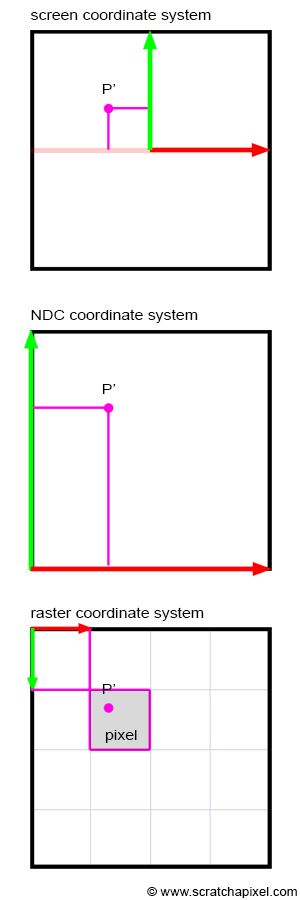
其实我们电脑的屏幕就相当于栅格空间,不同的分辨率代表着不同的水*像素数与竖直像素数,也就代表着不同的像素宽度与高度,代表着不同的栅格空间计算方法
注意我们这里的讨论实际上简化了屏幕坐标系与NDC坐标系,games101中的投影变换实际上就是直接从相机空间变换到了NDC空间或者说变换到了裁剪空间然后经过齐次除法到NDC空间,空间是三维的,因为我们不仅要完成投影,还需要记录点的z坐标信息来进行深度缓存等等,确定物体的先后关系:
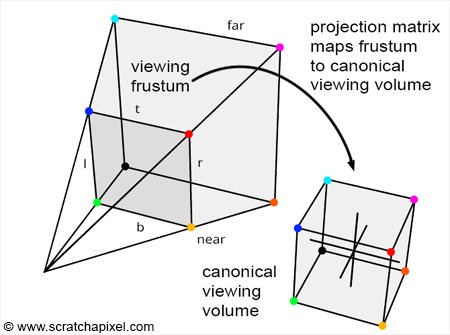
可以看到二维空间与三维空间的区别就是二维空间舍弃了z坐标,它们在xy坐标方面做的都是投影,三维空间相当于多做了z坐标的投影
注意games101其实并没有过多的讨论裁剪空间,而是推导了一个矩阵直接转换到NDC空间,这也是未来博客中要探讨的内容,同时z-fighting的现象也未提及(*远*面距离过大导致的问题)
在我们这里的讨论屏幕坐标系与NDC坐标系是二维的,这样可以把光栅化与光线追踪的visibility处理统一起来,因为光线追踪中我们并不需要使用投影矩阵,就不存在光栅化中的视锥体与立方体,只需要二维的屏幕空间。
光栅化做的就是从世界空间到栅格空间,实现每个物体的visibility,然后着色
而光线追踪做的是实现每个光线的可视化,然后着色,需要我们从栅格空间转换到世界空间。
光栅化中的空间变换
世界空间到观察空间或者说是摄像机空间:
这一步很简单,和games100课程中的一样,实际上就是进行坐标系变换,进行旋转与*移,值得注意的是默认,相机正对的是z的负半轴,所以我们可见的物体的z坐标也是负的
那么在进行从观察空间到屏幕空间的过程中,我们要进行投影,将3维的点投影到2维的屏幕上:
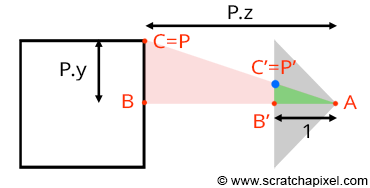
这样我们根据相似关系,可以得到屏幕空间与观察空间的xy坐标映射,注意这里我们假设和**面的距离是1,可以得到:
(begin{array}{l} P’.x = dfrac{P_{camera}.x}{P_{camera}.z} P’.y = dfrac{P_{camera}.y}{P_{camera}.z}. end{array})
但是注意我们之前提到过物体的z坐标是负的,所以这样进行除法会导致xy发生颠倒,因此,我们要再加上负号:
(begin{array}{l} P’.x = dfrac{P_{camera}.x}{-P_{camera}.z} P’.y = dfrac{P_{camera}.y}{-P_{camera}.z}. end{array})
之前提到过屏幕空间是有范围的,由宽度与高度决定,所以我们要加上这个限制
(text {visible} = begin{cases} yes & |P’.x| le {W over 2} text{ or } |P’.y| le {H over 2} no & text{otherwise} end{cases})
从屏幕空间到NDC空间,需要我们把原来在[-width/2]–[width/2]和[-height/2]到[height/2]之间的点转换到[0-1]的点(有的NDC空间采用的是[-1-1]):
(begin{array}{l} P’_{normalized}.x = dfrac{P’.x + width / 2}{ width } P’_{normalised}.y = dfrac{P’.y + height / 2}{ height } end{array})
从NDC空间到栅格空间,我们需要乘以像素宽度与高度,因为我们认为像素点是一个个小矩形来进行栅格化,并且取整,这一步也被称为viewport变换
(begin{array}{l} P’_{raster}.x = lfloor{ P’_{normalized}.x * text{ Pixel Width} }rfloor P’_{raster}.y = lfloor{ P’_{normalized}.y * text{Pixel Height} }rfloor end{array})
同时我们注意到栅格空间的y是向下的,所以改变方向取反:
(begin{array}{l} P’_{raster}.x = lfloor{ P’_{normalized}.x * text{ Pixel Width} }rfloor P’_{raster}.y = lfloor{ (1 – P’_{normalized}.服务器托管网y) * text{Pixel Height} }rfloor end{array})
以上我们就将三维空间中的点可视化到了二维空间中
光线追踪中的空间变换
针对光线追踪,我们需要的是可视化我们的光线,因为我们需要实际计算光线与物体相交,所以我们的光线需要世界坐标下的三维表示,简单来说一个光线可以如下定义:
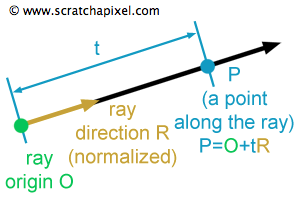
我们已经知道了O的位置,它就是坐服务器托管网标原点(0,0,0)
现在需要知道P的位置
现在考虑下面这张图:
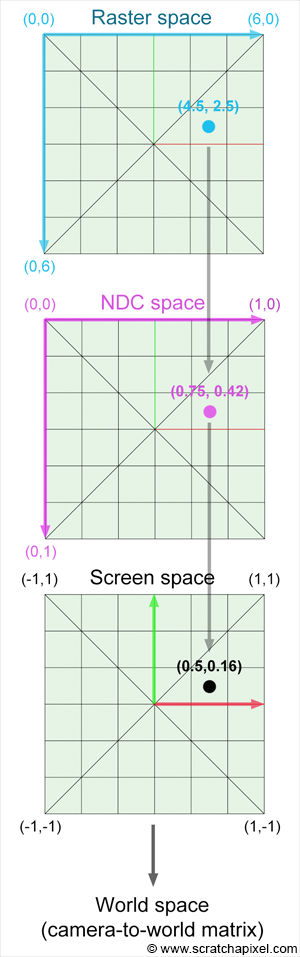
第一步转换到NDC空间:
(begin{array}{l}
PixelNDC_x = dfrac{(Pixel_x + 0.5)}{ImageWidth},
PixelNDC_y = dfrac{(Pixel_y + 0.5)}{ImageHeight}.
end{array})
注意这里我们只考虑光线穿过像素点的中心,所以我们要加上0.5,然后再分别除以栅格空间的宽度与高度
第二步转换到屏幕空间:
注意屏幕空间的y轴发生了反转,同时由于我们是将原本的图像压缩到了-1-1的这个空间中,所以我们现在要将其还原回去,即宽度从[-1–1]转换成[-width/2—width/2],高度同理,我们使用宽高比以及fov角度来表示就可以得到:
(begin{array}{l} PixelCamera_x = (2 * {PixelNDC_x } – 1) * ImageAspectRatio * tan(dfrac{alpha}{2}), PixelCamera_y = (1 – 2 * {PixelNDC_y }) * tan(dfrac{alpha}{2}). end{array})
其中tan(a/2)表示图像高度的一半,因为我们在这里假设**面坐标是-1
最后转换到世界空间中,只需要加入z坐标-1,然后从相机空间转换到世界空间即可
上述过程也就是games101第五次作业求光线的实现
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: 大健康产业中医药文化博览会暨全国中小企业数字化转型交流会举办
为了推动全国中小企业数字化转型和高质量数实融合发展,全面推进太白山景区数实融合产业实践,由太白山旅游区管委会、陕西省智库服务中心指导,陕西醉美太白山水文化产业发展有限公司,悠然云居健康科技(陕西)有限公司、上海无界SaaS陕西中心、慧了上医生活共享联盟联合主办…

