games101-2 透视深度插值矫正与抗锯齿分析 - 服务器托管|北京服务器租用|机房托管租用|IDC托管租用|机房机柜带宽租用-价格及费用咨询

透视深度插值矫正与抗锯齿分析
- 深度插值的差错原因
- 透视深度插值公式推导
- games101中的错误
- msaa与ssaa简要定义
- games101中ssaa的实现
- games101中msaa的实现

深度插值的差错原因

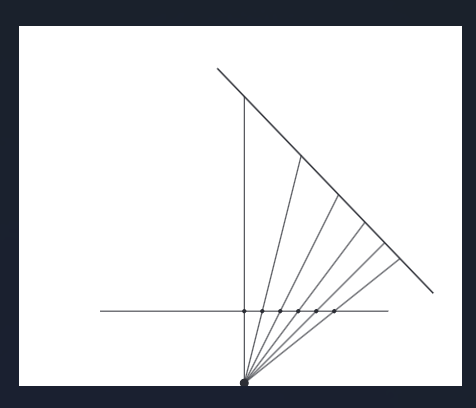
当投影的图形与投影的平面不平行时，这时进行透视投影，从上图中可以看出，投影平面上的线段时均匀的，但是在原图形上的线段是非均匀的，这只是一个例子，但也可以看出投影会导致图形的变形，在我们利用重心坐标，进行深度插值时原空间中的重心坐标会发生变形，导致我们得到的深度不是正确的，这一点在对纹理坐标进行插值时尤其明显

透视深度插值公式推导

虽然在原空间与投影平面上的三角形可能发生变形，但是它们的重心坐标依然满足一定的关系：
投影平面：
(1 = alpha^{‘} +beta^{‘} +gamma^{‘})

原空间：
(1 = alpha +beta +gamma)

现在我们只有投影平面上三角形的bounding box中一个个像素点，我们想要得到这个像素点真实的深度值，假设一个像素点真实的深度值为(Z),三角形三个顶点真实的深度值分别为(Z_{a},Z_{b},Z_{c})，我们对第一个式子进行恒等变形：

$frac{Z}{Z} = frac{Z_{a}}{Z_{a}}alpha^{‘} + frac{Z_{b}}{Z_{b}}beta^{‘} + frac{Z_{c}}{Z_{c}}gamma^{‘} $

进一步变换得到：
(Z = (frac{Z}{Z_{a}}alpha^{‘})Z_{a} + (frac{Z}{Z_{b}}beta^{‘})Z_{b} + (frac{Z}{Z_{c}}gamma^{‘})Z_{c})

我们对照原空间的深度重心插值公式：
(Z = alpha Z_{a} + beta Z_{b} + gamma Z_{c})

可以得到:
(alpha = frac{Z}{Z_{a}}alpha^{‘})
(beta = frac{Z}{Z_{b}}beta^{‘})
(gamma = frac{Z}{Z_{c}}gamma^{‘})

我们再代入之前的第二个式子：
(1 = frac{Z}{Z_{a}}alpha^{‘} + frac{Z}{Z_{b}}beta^{‘} + frac{Z}{Z_{c}}gamma^{‘})

两边同时除以(Z):
$frac{1}{Z} = frac{1}{Z_{a}}alpha^{‘} + frac{1}{Z_{b}}beta^{‘} + frac{1}{Z_{c}}gamma^{‘} $

我们可以进一步考虑更一般的情况，对任意属性(uv坐标颜色法线等)使用重心坐标进行插值：
(I = alpha I_{a} + beta I_服务器托管网{b} + gamma I_{c})

(I = Z(alpha^{‘}frac{I_{a}}{Z_{a}} + beta^{‘}frac{I_{b}}{Z_{b}} + gamma^{‘}frac{I_{c}}{Z_{c}} ))

games101中的错误

有了上述理论基础，我们再来看看games101中的实现：

auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0/(a服务器托管网lpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();

注意在前面：

auto v = t.toVector4();

games101将一个三维向量拓展为四维向量，理论上一个像素点的坐标应该是(x,y,z,w)，其中x，y代表投影的xy坐标，z代表压缩之后的z值，一般在[-1,1]或者[0,1]或者[n,f]之间，w一般用于存储原空间真实的深度值，但是上述拓展默认将w设置为1，w存储的不是真实的深度值，因此：

float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());

这一步使用的深度值是错误的

假如是正确的，其实这一步得到的w_reciprocal已经是正确的深度矫正值，也不需要在后面再求z值

但是最终结果我们也没有发现明显的错误，可以认为即使使用错误的深度值，对最终结果也影响不大

msaa与ssaa简要定义

MSAA：多重采样抗锯齿是一种选择性的抗锯齿技术，它在渲染图像时对特定部分进行多次采样。通常，它会对几何边缘周围进行多次采样，以减少锯齿状边缘的出现。
SSAA：超级采样抗锯齿是一种全局的抗锯齿技术，它通过在整个图像上进行更高分辨率的采样，然后缩放到目标分辨率，从而减少锯齿和增强图像的质量。

games101中ssaa的实现

ssaa实现的是更高分辨率的采样，为了实现这一点我们需要为每个采样点都维护深度表与颜色表，在对每个采样点进行覆盖检测以及深度检测之后，将采样点的颜色进行平均，设置为像素点颜色：

for(int x=min_x; x

games101中msaa的实现

msaa与ssaa类似，也是对四个采样点的颜色进行混合，也需要对采样点进行覆盖以及深度检测，不过不同的时，msaa会记录深度的变化，只有在深度发生变化，认为检测到边缘的时候，才会进行shading，并且不需要维护颜色表，减少了时间以及空间开销：

for(int x=min_x; x 0){
                int ind = get_index(x,y);
                Eigen::Vector3f p;
                p

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.fwqtg.net

相关推荐: Java基础语法(超级详细哦!!!)

1. 注释注释是对代码的解释和说明文字。 Java中的注释分为三种：单行注释： // 这是单行注释文字多行注释： /* 这是多行注释文字这是多行注释文字这是多行注释文字 */ 注意：多行注释不能嵌套使用。文档注释（暂时用不到）： /** 这是多行注…