leetCode 137. 只出现一次的数字 II（拓展篇） + 模5加法器 + 真值表（数字电路）

leetCode 137.只出现一次的数字 II 有其他的题解可看我的往期文章：

leetCode 137. 只出现一次的数字 II + 位运算 + 模3服务器托管网加法器 + 真值表（数字电路） + 有限状态机-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134138112?spm=1001.2014.3001.5501

关于 leetCode 137.只出现一次的数字 II，参考灵神的解法做的思路分析：

0->1->2->0->1->2->...
(0,0)->(0,1)->(1,0)->(0,0)->(0,1)->(1,0)->...
>>分析
其中有大量 0 和 1 之间的转换,可以用异或运算实现
    ① a=a^1
    ② b=b^1
方式1：「同时计算」
    a = a^x & a|b
    b = b^x & (~a)

方式2：「分别计算」
    先计算b,再计算a(思路：b在同时计算的时候式子比较简洁，可用新b来参与计算a)
    b = b^x & (~a)
    a = a^x & (~b)

    >>思路和过程分析
        (0,0)->(0,1)->(1,0)
        (1)先算b:b = b^x & (~a)，可得
        (0,1)->(0,0)->(1,0)

       服务器托管网 (2)再算a
        (0,1)->(0,0)->(1,0)
        // 1.调换位置
        (1,0)->(0,0)->(0,1)
        // 2.调整画法
        (0,0)->(0,1)->(1,0)

        // 计算b前的状态转换图
        (0,0)->(0,1)->(1,0)

        //最后的得到的状态转换图与计算b前的状态转换图是等价的，即若使用计算后的新b,则可以通过相同的公式计算a
        a = a^x & (~b)

1.方式1：

class Solution {
public:
    // 模3加法 方法2：用位运算实现
    int singleNumber(vector& nums) {
        int a=0,b=0;
        for(const int& x:nums) {
            int tmp_a = a;
            a = (a^x) & (a|b);
            b = (b^x) & (~tmp_a);
        }
        return b; 
    }
};

2.方式2：

class Solution {
public:
    // 模3加法 方法2：用位运算实现
    int singleNumber(vector& nums) {
        int a=0,b=0;
        for(const int& x:nums) {
            b = (b^x) & (~a);
            a = (a^x) & (~b);
        }
        return b; 
    }
};

【灵茶山艾府出的思考题】（137. 只出现一次的数字 II – 力扣（LeetCode））：

• 如果把转换规则改成 0→2→1→0→2→1→⋯，对应的代码应该如何修改呢？
• 如果改成除了一个数字出现一次，其余数字均出现 5 次呢？

（1）第一题解法：

这个是我的解题思路：
// 第一种方法
0 → 2 → 1 → 0 → 2 → 1 → ⋯
(0,0) -> (1,0) -> (0,1) -> (0,0) -> ...
>>分析
其中有大量 0 和 1 之间的转换,可以用异或运算实现
    ① a=a^1
    ② b=b^1
    
(1)先算a，a = a^x & (~b);可得
(1,0) -> (0,0) -> (0,1) -> (1,0) -> ...

(2)再算b
(1,0) -> (0,0) -> (0,1) 
// 1.调换位置
(0,1) -> (0,0) -> (1,0) 
// 2.调整画法
(0,0)->(1,0)->(0,1)

// 计算a前的状态转换图
(0,0)->(1,0)->(0,1)

// 最后的得到的状态转换图与计算a前的状态转换图是等价的，即若使用计算后的新a,则可以通过相同的公式计算b
b = b^x & (~a);

// 第二种方法
0->1->2->0->1->2->...
(0,0)->(0,1)->(1,0)->(0,0)->(0,1)->(1,0)->...

0 → 2 → 1 → 0 → 2 → 1 → ⋯
(0,0) -> (1,0) -> (0,1) -> (0,0) -> ...

仔细观察这个区别，其实就是a和b调换了，所以可以先计算a,再计算b
a = a^x & (~b);
b = b^x & (~a);

（2）第二题解法：

1.「同时计算」

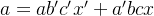
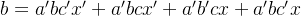
化简 b 和 c：

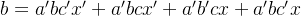
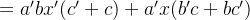
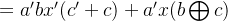
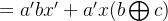
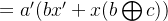
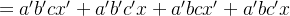
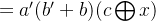
#include 
#include 
using namespace std;

int singleNumber(vector nums) {
	int i, a, b, c, tmpa, tmpb, tmpc;
	a = 0;
	b = 0;
	c = 0;
	for (const int& x : nums) {
		// 第一种
		tmpa = a;
		tmpb = b;
		tmpc = c;
		a = a & ~tmpb & ~tmpc & ~x | ~a & tmpb & tmpc & x;
		b = ~tmpa & b & (~tmpc | tmpc) | ~tmpa & x & (b ^ tmpc);
		c = ~tmpa & (c ^ x);
	}
	return c;
}

int main() {
	vector nums{3,3,3,3,3,2,2,2,2,2,6,6,6,6,6,4,4,4,10,4,4 };
	cout

2.「分别计算」

发现上面化简 c 后，式子很简洁：

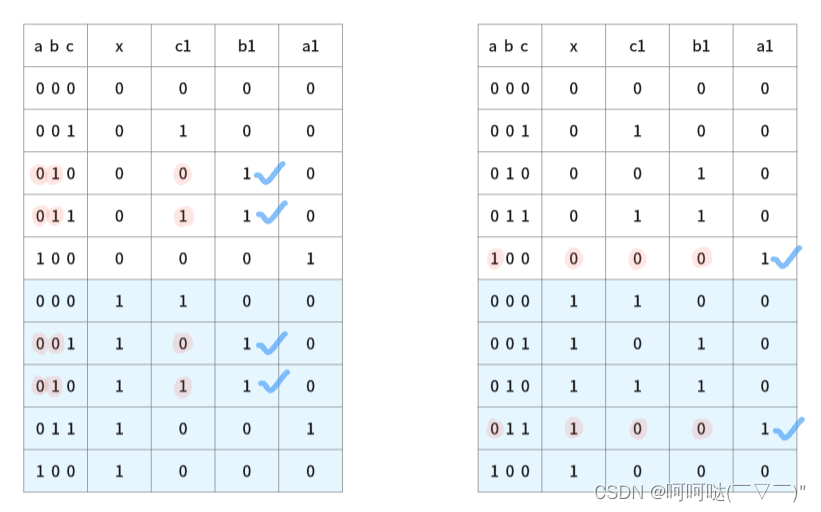
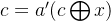
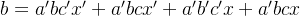
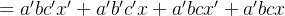
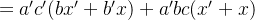
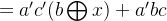
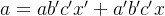
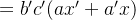
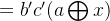
#include 
#include 
using namespace std;

int singleNumber(vector nums) {
	int i, a, b, c, tmpa, tmpb, tmpc;
	a = 0;
	b = 0;
	c = 0;
	for (const int& x : nums) {
		// 第二种
		c = ~a & (c ^ x);
		b = ~a & ~c & (b ^ x) | ~a & b & c;
		a = ~b & ~c & (a ^ x);
	}
	return c;
}

int main() {
	vector nums{3,3,3,3,3,2,2,2,2,2,6,6,6,6,6,4,4,4,10,4,4 };
	cout

我的解法，不知道是否正确，仅供参考！

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net

相关推荐: aruba无线控制器配置和license备份

备份配置 备份系统 导出备份到FTP 导出license到FTP 服务器托管网服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net 机房租用，北京机房租用，IDC机服务器托管网房托管， http://www.fwqtg.net相关推…