Leetcode.2477 到达首都的最少油耗

题目链接

Leetcode.2477 到达首都的最少油耗 rating : 2012

题目描述

给你一棵

n

n

n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从

0

0

0 到

n

−

1

n – 1

n−1 ，且恰好有

n

−

1

n – 1

n−1 条路。

0

0

0 是首都。给你一个二维整数数组

r

o

a

d

s

roads

roads ，其中

r

o

a

d

s

[

i

]

=

[

a

i

,

b

i

]

roads[i] = [a_i, b_i]

roads[i]=[ai​,bi​] ，表示城市

a

i

a_i

ai​ 和

b

i

b_i

bi​ 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数

s

e

a

t

s

seats

seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

示例 1：

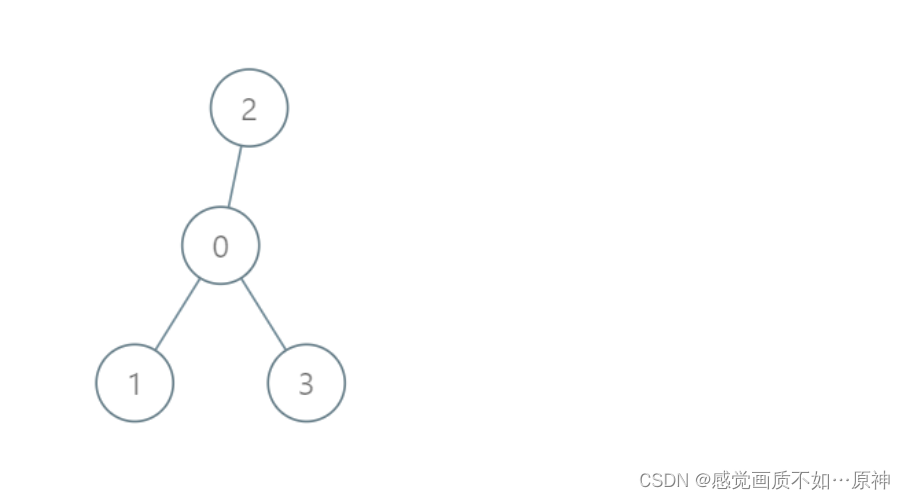
输入：roads = [[0,1],[0,2],[0,3]], seats = 5
输出：3
解释：

• 代表 1 直接到达首都，消耗 1 升汽油。
• 代表 2 直接到达首都，消耗 1 升汽油。
• 代表 3 直接到达首都，消耗 1 升汽油。 最少消耗 3 升汽油。

示例 2：

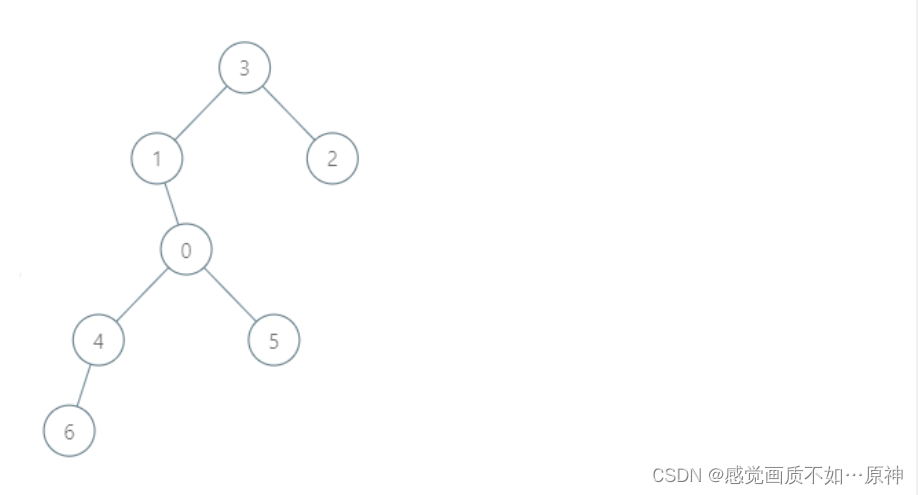
输入：roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出：7
解释：

• 代表 2 到达城市 3 ，消耗 1 升汽油。
• 代表 2 和代表 3 一起到达城市 1 ，消耗 1 升汽油。
• 代表 2 和代表 3 一起到达首都，消耗 1 升汽油。
• 代表 1 直接到达首都，消耗 1 升汽油。
• 代表 5 直接到达首都，消耗 1 升汽油。
• 代表 6 到达城市 4 ，消耗 1 升汽油。
• 代表 4 和代表 6 一起到达首都，消耗 1 升汽油。 最少消耗 7 升汽油。

示例 3：

输入：roads = [], seats = 1
输出：0
解释：没有代表需要从别的城市到达首都。

提示：

• 1

  ≤

  n

  ≤

  1

  0

  5

  1 leq n leq 10^5

  1≤n≤105

• $roads.length=n-1$
• $roads[i].length=2$

• 0

  ≤

  a

  i

  ,

  b

  i

  0≤ai​,bi​n

• a

  i

  ≠

  b

  i

  a_i neq b_i

  ai​=bi​

• $roads$

• 1

  ≤

  s

  e

  a

  t

  s

  ≤

  1

  0

  5

  1 leq seats leq 10^5

  1≤seats≤105

解法：dfs + 贪心

越靠近起点

0

0

0 的边，经过的车越多，所消耗的燃料也就越多。

由于我们求得是消耗的最少的燃料，假设以点

v

v

v 为根节点的子树上的所有节点都要经过边

{

u

,

v

}

{服务器托管网 u,v}

{u,v} 到点

u

u

u，子树

v

v

v 的节点总数为

c

n

t

v

cnt_v

cntv​，那么要让

c

n

t

v

cnt_v

cntv​ 个节点都被移动到 点

u

u

u ，最少需要

⌈

c

n

t

v

s

e
服务器托管网

a

t

s

⌉

lceil frac{cnt_v}{seats} rceil

⌈seatscntv​​⌉ 辆车，为了用尽可能少的燃料，所以我们直接用

⌈

c

n

t

v

s

e

a

t

s

⌉

lceil frac{cnt_v}{seats} rceil

⌈seatscntv​​⌉ 辆车。

那么对于 边

{

u

,

v

}

{ u,v}

{u,v}，一共有

⌈

c

n

t

v

s

e

a

t

s

⌉

lceil frac{cnt_v}{seats} rceil

⌈seatscntv​​⌉ 辆车通过了这条边，所以一共要消耗

⌈

c

n

t

v

s

e

a

t

s

⌉

lceil frac{cnt_v}{seats} rceil

⌈seatscntv​​⌉ 升燃料。

我们直接从 起点

0

0

0 开始遍历所有的边，记录总的燃料即可。

时间复杂度 ：

O

(

n

)

O(n)

O(n)

C++代码：

using LL = long long;

class Solution {
public:
    long long minimumFuelCost(vectorvectorint>>& roads, int seats) {
        unordered_mapint,vectorint>> g;
        int n = 0;
        for(auto &e:roads){
            int a = e[0] , b = e[1];
            n = max({a,b,n});
            g[a].push_back(b);
            g[b].push_back(a);
        }

        n++;
        //s[i] 就是以 i 为根节点的节点总数
        vectorint> s(n);
        LL ans = 0;

        functionint(int,int)> dfs = [&](int u,int fa) ->int{
            s[u] = 1;
            for(auto v:g[u]){
                if(v == fa) continue;
                s[u] += dfs(v,u);
            }
            //不统计根节点
            if(u != 0) ans += (s[u] + seats - 1) / seats;
            return s[u];
        };

        dfs(0,-1);
       

        return ans;
    }
};

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net