论文参考信号处理中提升方案提出双向池化操作LiftPool,不仅下采样时能保留尽可能多的细节,上采样时也能恢复更多的细节。从实验结果来看,LiftPool对图像分类能的准确率和鲁棒性都有不错的提升,而对语义分割的准确性更能有可观的提升。不过目前论文还在准备开源阶段,期待开源后的复现,特别是在速度和显存方面结果
来源:晓飞的算法工程笔记 公众号
论文: LiftPool: Bidirectional ConvNet Pooling

- 论文地址:https://arxiv.org/abs/2104.00996
- 论文代码:https://github.com/jiaozizhao/LiftPool/
Introduction
空服务器托管间池化是卷积网络中很重要的操作,关键在于缩小分辨率的同时保留最重要的特征值,方便后续的模型辨别。简单的池化操作,如最大池化和平均池化,不仅池化时忽略了局部特性,还不支持逆向恢复丢失的信息。为此,论文提出了双向池化层LiftPool,包含保留细节特征的下采样操作LiftDownPool以及产生精细特征图的上采样操作LiftUpPool。

LiftPool的灵感来自于信号处理中的提升方案(Lifting Scheme),下采样时将输入分解成多个次频带(sub-band),上采样时能够完美地逆向恢复。如图1所示,LiftDownPool产生四个次频带,其中LL次频带是去掉细节的输入近似,LH、HL和HH则分别包含水平、垂直和对角方向的细节信息。用户可以选择一个或多个次频带作为输出,保留其它次频带用于恢复。LiftUpPool根据次频带恢复上采样输入,对比MaxUpPool的效果,LiftUpPool则能产生更精细的输出。
Methods
下采样特征图时,池化操作核心在于减少下采样造成的信息损失,而信号处理中的提升方案(Lift Scheme)恰好能满足这一需求。提升方案利用信号的相关结构,在空间域构造其下采样的近似信号以及多个包含细节信息的次频带(sub-band),在逆转换时能完美重构输入信号。借用提升方案,论文提出了双向池化层LiftPool。
LiftDownPool
-
LiftDownPool-1D
以一维信号(x=[x_1, x_2, x_3, cdots, x_n], x_ninmathbb{R})为例,LiftDownPool将其分解成下采样近似信号(s)和差分信号(d):
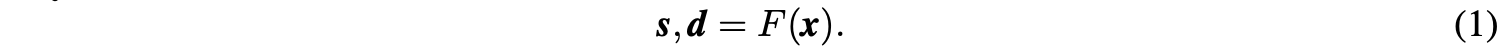
其中(F(cdot)=f_{update}circ f_{predict}circ f_{split}(cdot))包含3个函数,(circ)表示函数组合。

LiftDownPool-1D的整体过程如图2所示,包含以下步骤:
- Split操作(f_{split}:xto (x^e, x^o)):将信号(x)分成偶数下标组(x^e=[x_2, x_4, cdots, x_{2k}])和奇数下标组(x^o=[x_1, x_3, cdots, x_{2k+1}]),这两组信号是密接相关的。
- Predict操作(f_{predict}:(x^e, x^o)to d):给定信号集(x^e)和(x^o),设想的是(x服务器托管^e)可通过预测器(mathcal{P}(cdot))转换得到(x^o)。这里不要求预测器是完全准确的,定义两者间的差分信号(d)为:
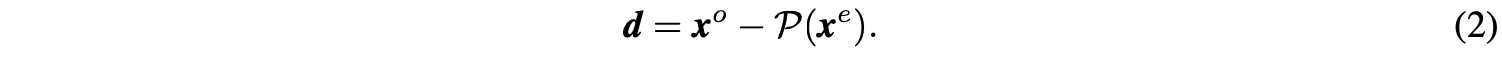
公式2只保留了少量的细节差异信息,功能等价于对(x)进行了高通滤波。 - Update操作(f_{update}:(x^e, d)to s):因为(x^e)是从(x)简单下采样而来的,直接将(x^e)作为(x)的近似会有严重的混叠现象(采样导致信号减弱,具体可见原文附录),而且(x^e)的均值与(x)的均值也不一样。为此,可通过对(x^e)加上(mathcal{U}(d))得到平滑版本(s):
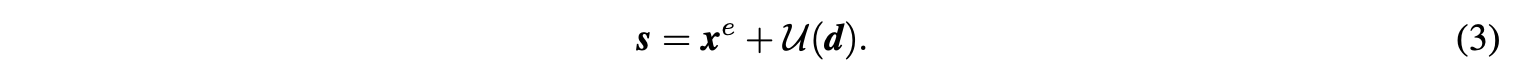
公式3保留了尽可能多的输入信息,功能等价于对(x)进行低通滤波,因此可将低通过滤后的(s)作为原信号的近似。
实际上,经典的提升方案就是由低通滤波和高通滤波来完成的,通过预设的滤波器将图片分解成四个次频带。但一般来说,以预设滤波器的形式定义(mathcal{P}(cdot))和(mathcal{U}(cdot))是很难的。为此,Zheng等人提出通过网络的反向传播来学习滤波器。借用此思路,论文通过1D卷积+非线性激活来实现LiftDownPool中的(mathcal{P}(cdot))和(mathcal{U}(cdot))功能:
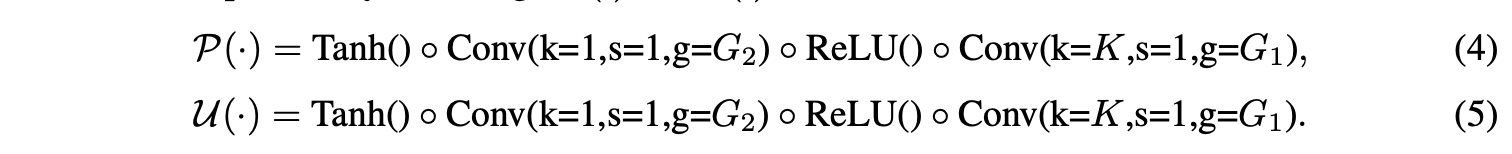
为了能够更好地进行端到端地训练,需要对最终的损失函数添加两个约束。首先,(s)是从(x^e)变化得到的,基本上要跟(x^e)相似,添加正则项(c_u)最小化(s)和(x^o)的L2-norm距离:

另外,(mathcal{P}(cdot))的设想是将(x^e)转换为(x^o),所以添加正则项(c_p)最小化细节差异(d):

完整的损失函数为:
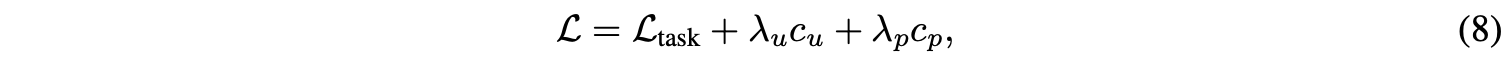
(mathcal{L}_{task})为特定任务的损失函数,如分类或语义分割损失。设置(lambda_u=0.01)和(lambda_p=0.1),能够给模型带来不错的正则化效果。
-
LiftDownPool-2D
LiftDownPool-2D可分解成几个LiftDownPool-1D操作。根据标准提升方案,先在水平方向执行LiftDownPool-1D获得(s)(水平方向的低频)以及(d)(水平方向的高频)。随后对这两部分分别执行垂直方向的LiftDownPool-1D,(s)被进一步分解成LL(垂直和水平方向的低频)和LH(垂直方向的低频和水平方向的高频),而(d)则被进一步分解成HL(垂直方向的高频和水平方向的低频)和HH(垂直和水平方向的高频)。
用户可灵活选择其中一个或多个次频带作为结果,保留其它次频带用于恢复。一般来说,LiftDownPool-1D可以进一步泛化到n维信号。

图3为VGG13的首个LiftDownPool层的几个特征输出,LL特征更平滑,细节较少,LH、HL和HH则分别捕捉了水平方向、垂直方向和对角方向的细节。
LiftUpPool
LiftUpPool继承了提升方案的可逆性。继续以1D信号为例,LiftUpPool可从(s,d)中恢复上采样信号(x):
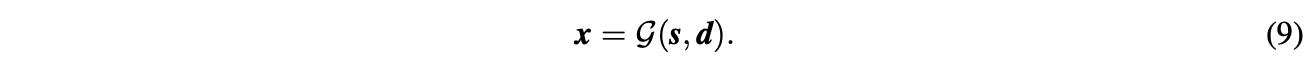
(mathcal{G}(cdot)=f_{merge}circ f_{predict}circ f_{update}(cdot))包含update、predict、merge函数,即(s,dto x^e,dto x^e,x^oto x):
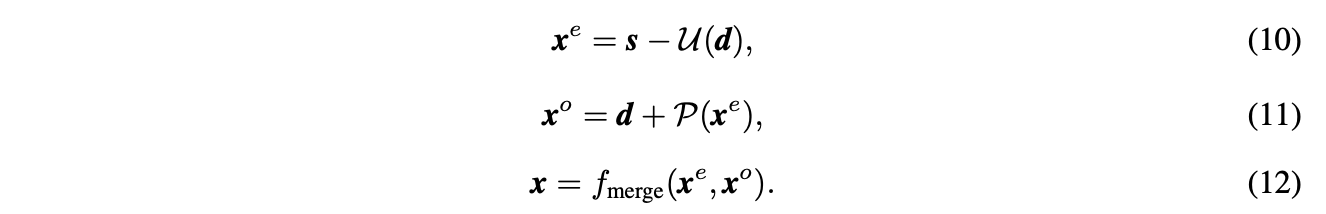
通过上述公式获得(x^e)和(x^o),进而合成(x),得到包含丰富信息的上采样特征图。
上采样在image-to-image转换中经常使用,比如语义分割,超分辨率和图片上色等任务。但目前大多数池化操作是不可逆的,比如MaxPool上采样的输出较为稀疏且损失大部分的结构信息。而LiftUpPool能对LiftDownPool的输出进行逆转换,借助次频带产出更好的输出。
Compare with MaxPool
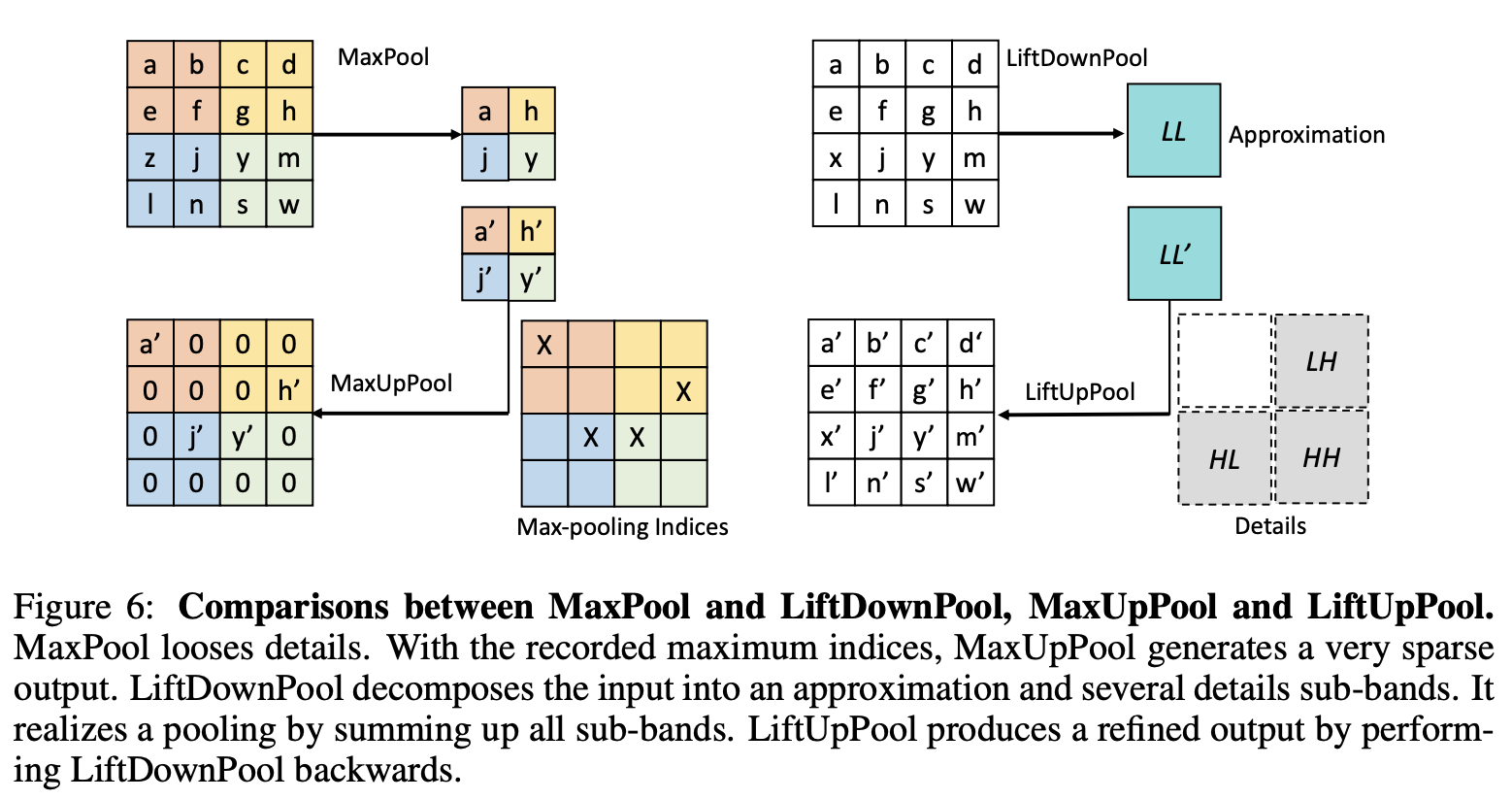
以kernel size=2、stride=2的池化为例,LiftPool和MaxPool的逻辑如图6所示。
-
LiftDownPool vs. MaxPool
Maxpool选择局部最大值作为输出,会丢失75%的信息,这其中很可能包含了跟图像识别相关的重要信息。
LiftDownPool将特征图分解成次频带LL、LH、HL和HH,其中LL为输入的近似,其它为不同方向的细节信息。LiftDownPool将所有次频带相加作为输出,包含了近似信息和细节信息,能够更高效地用于图像分类。
-
LiftUpPool vs. MaxUpPool
MaxPool是不可逆的,通过记录的的最大值下标进行MaxUpPool。MaxUpPool将输出的特征图的特征值对应回下标位置,其余均为零,所以恢复的特征图十分稀疏。
LiftDownPool是可逆的,根据提升方案的属性对LiftDownPool进行反向恢复,而且LiftUpPool能生成包含记录的细节的高质量结果。
Experiment

在CIFAR-100上对比次频带和正则项效果。
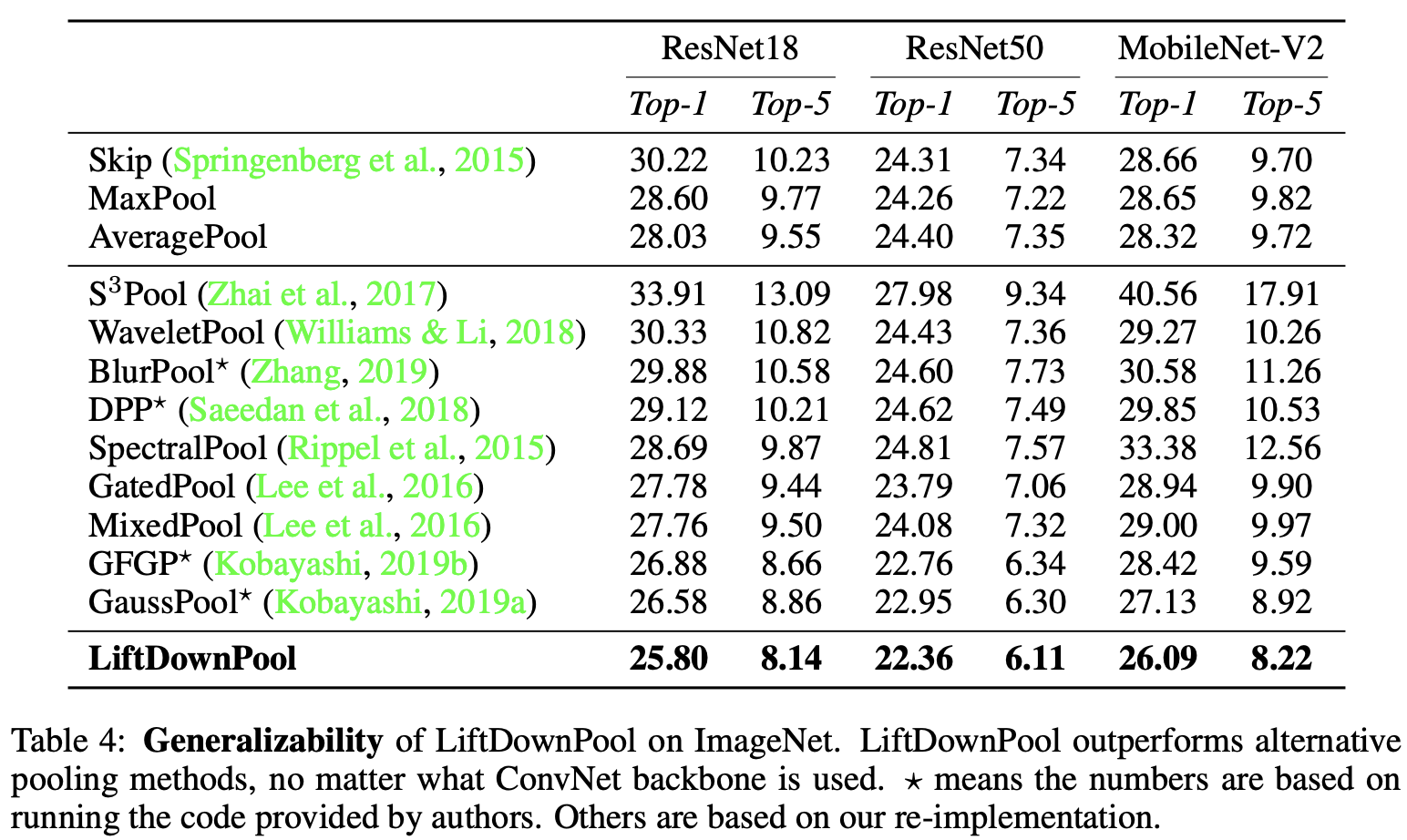
在ImageNet上,搭配不同主干网络上进行对比。

进行抗干扰数据集测试对比。

不同数据集上的语义分割性能对比。

语义分割上采样结果对比。
Conclusion
论文参考信号处理中提升方案提出双向池化操作LiftPool,不仅下采样时能保留尽可能多的细节,上采样时也能恢复更多的细节。从实验结果来看,LiftPool对图像分类能的准确率和鲁棒性都有不错的提升,而对语义分割的准确性更能有可观的提升。不过目前论文还在准备开源阶段,期待开源后的复现,特别是在速度和显存方面结果。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】

服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net

