MATLAB强大的符号运算基于符号运算工具箱,具体请见其官方文档.
创建符号变量
创建符号数字
使用sym函数可以创建符号数字.使用符号数字可以精确地保存无理数,不会产生误差.
sym(1/3) % 得到 1/3
1/3 % 得到 0.3333将无理数保存为符号数字可以避免将其转换为浮点数的误差:
- 使用符号数字计算sin ( ) sin(pi)sin()
sin(sym(pi)) % 得到 0
sin(pi) % 得到 1.2246e-16- 使用符号数字计算 = 1 + 5 2 phi = frac{1+sqrt{5}}{2}=21+5
symphi = (1 + sqrt(sym(5)))/2; % 得到 5^(1/2)/2 + 1/2
symf = symphi^2 - symphi - 1; % 得到 (5^(1/2)/2 + 1/2)^2 - 5^(1/2)/2 - 3/2
numphi = (1 + sqrt(5))/2; % 得到 1.6180
numf = numphi^2 - numphi - 1; % 得到 0创建符号变量
使用sym和syms可以创建符号变量,区别在于:
-
sym每次只能创建一个符号变量,而syms一次可以创建多个符号变量.
syms a % sym命令只能创建一个符号变量
syms b c d % syms命令可以创建多个符号变量- 若所指定的符号变量已存在,
sym不会保留其原有的值,而syms会清空其值.
syms x y
f = x+y; % 隐式创建符号变量f
sym f % 不清空变量f原有的值,即f = x + ysyms x y
f = x+y; % 隐式创建符号变量f
syms f % 清空变量f原有的值,即f = f- 使用
sym可以创建符号变量矩阵.
A = sym('a', [2 5]) % 创建一个2*5的符号变量矩阵
whos得到的输出如下:
A =
[ a1_1, a1_2, a1_3, a1_4, a1_5]
[ a2_1, a2_2, a2_3, a2_4, a2_5]
Name Size Bytes Class Attributes
A 2x5 112 sym联合使用sym和syms可以快速创建一系列带下标的变量
clear all
syms(sym('a', [1 5]))
whos得到输出如下:
Name Size Bytes Class Attributes
a1 1x1 8 sym
a2 1x1 8 sym
a3 1x1 8 sym
a4 1x1 8 sym
a5 1x1 8 sym符号运算
符号表达式的化简与代入
符号表达式的化简
使用simplify()函数可以化简符号表达式.
syms x a b c
simplify(sin(x)^2 + cos(x)^2); % 得到 1
simplify(exp(c*log(sqrt(a+b)))); % 得到 (a + b)^(c/2)表达式化简的标准是不确定的,下面三个函数分别按照不同标准化简表达式:
-
expand()函数可以展开表达式
syms x
f = (x ^2- 1)*(x^4 + x^3 + x^2 + x + 1)*(x^4 - x^3 + x^2 - x + 1);
expand(f); % 得到 x^10 - 1-
factor()函数可以分解因式
syms x
g = x^3 + 6*x^2 + 11*x + 6;
factor(g); % 得到 (x + 3)*(x + 2)*(x + 1)-
horner()函数可以将多项式变为嵌套形式
syms x
h = x^5 + x^4 + x^3 + x^2 + x;
horner(h); % 得到 x*(x*(x*(x*(x + 1) + 1) + 1) + 1)符号表达式的代入
使用sub(expr, old, new)函数可以将符号表达式expr中的old替换为new.
syms x
f = 2*x^2 - 3*x + 1;
subs(f, 1/3) % 得到 2/9syms x y
f = x^2*y +服务器托管网 5*x*sqrt(y);
subs(f, x, 3); % 得到 9*y + 15*y^(1/2)求方程的解析解
使用solve(eqn,var)和solve(eqns,vars)可以求取方程式的解析解.
解单变量方程
使用==定义一个方程,并对其调用solve函数求解.
syms x
eqn = x^3 - 6*x^2 == 6 - 11*x;
solve(eqn); % 得到 [1 2 3]若不指定==符号右边的值,则默认等式右边为0.
syms x
eqn = x^3 - 6*x^2 + 11*x - 6;
solve(eqn); % 得到 [1 2 服务器托管网3]解多变量方程
对于多变量方程,我们需要指定针对哪个变量进行求解.
syms x y
eqn = [6*x^2 - 6*x^2*y + x*y^2 - x*y + y^3 - y^2 == 0];
solve(eqn, y); % 得到 [1, 2*x, -3*x]解方程组
向solve()函数传入方程组可以解方程.
syms u v
eqns = [2*u + v == 0, u - v == 1];
S = solve(eqns,[u v]);可以通过变量名索引方程的解,并可以将该解代入其他表达式中.
S.u; % 得到 1/3
S.v; % 得到 -2/3
subs(3*v + u, S); % 得到 -5/3符号微积分运算
求极限
使用limit(expr, var, a)函数可以求取符号表达式expr在变量var趋近于a时的极限,添加参数'left'或'right'可以指定左极限或右极限.
syms x;
expr = 1/x;
limit(expr,x,0); % 得到NaN
limit(expr,x,0,'left'); % 得到-Inf
limit(expr,x,0,'right'); % 得到Inf微分
使用diff(expr, var, n)函数可以求取符号表达式expr对变量var的n阶微分.
syms a b c x;
expr = a*x^2 + b*x + c;
diff(expr, a); % 得到 x^2
diff(expr, b); % 得到 x
diff(expr, x); % 得到 b + 2*a*x
diff(expr, x, 2); % 得到 2*a积分
使用int(expr, var)函数可以求取符号表达式expr对变量var的不定积分.使用int(expr, var, [a, b])函数可以指定上下限求定积分,a和b可以是符号表达式.
syms x a b
expr = -2*x/(1+x^2)^2;
int(expr, x); % 得到 1/(x^2 + 1)
int(expr, x, [1, 2]); % 得到 -0.3
int(expr, x, [1, Inf]); % 得到 -0.5
int(expr, x, [a, b]); % 得到 1/(b^2 + 1) - 1/(a^2 + 1)对于一些函数,MATLAB不能求出其积分,这时MATLAB会返回一个未解析(unsolved)的积分形式.
syms x
int(sin(sinh(x))); % 一个无解的积分,MATLAB返回 int(sin(sinh(x)), x)级数求和
使用symsum(expr, k, [a b])计算级数expr的索引k从a到b的加和.
syms k x
symsum(k^2, k) % 得到 k^3/3 - k^2/2 + k/6
symsum(k^2, k, [0 10]) % 得到 385
symsum(x^k/factorial(k),k,1,Inf) % 得到 exp(x) - 1泰勒展开
使用taylor(expr,var,a)计算表达式expr在var=a处的泰勒级数.
syms x
taylor(exp(x)) % 得到 x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1
taylor(sin(x)) % 得到 x^5/120 - x^3/6 + x
taylor(cos(x)) % 得到 x^4/24 - x^2/2 + 1绘制图像
可以对符号表达式绘制图像,常用的绘图函数如下:
|
函数 |
作用 |
|
|
绘制符号表达式的二维线图像 |
|
|
绘制符号表达式的三维线图像 |
|
|
绘制符号表达式的极坐标线图像 |
|
|
绘制网状面图像 |
|
|
绘制带颜色的面图像 |
|
|
绘制轮廓图像 |
|
|
绘制隐含函数关系的图像 |
- 下面例子展示二维和三维线图像的绘制
subplot(1, 2, 1)
syms x
f = x^3 - 6*x^2 + 11*x - 6;
fplot(f, x)
subplot(1, 2, 2)
syms t
fplot3(t^2*sin(10*t), t^2*cos(10*t), t)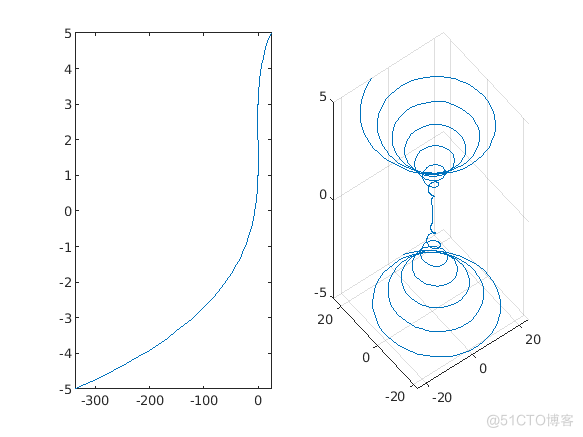
- 下面例子演示三维面的绘制
syms x y
fsurf(x^2 + y^2)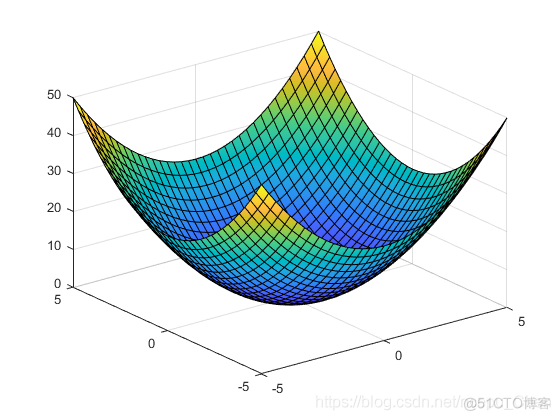
- 下面例子演示隐含函数关系图像的绘制
syms x y
eqn = (x^2 + y^2)^4 == (x^2 - y^2)^2;
fimplicit(eqn, [-1 1])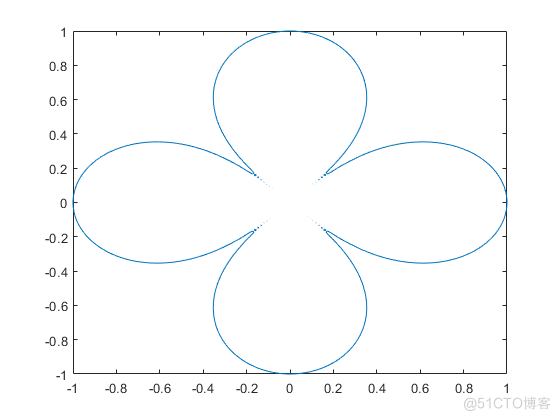
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: 多账号管理:如何保护多个Wish店铺免受关联风险
在如今的电商市场上,开设多个Wish店铺已成为许多商家实现成功的策略之一。Wish作为全球知名的电商平台,拥有庞大的用户群体,为商家提供了一个广阔的销售平台。然而,随之而来的是开店铺的风险,特别是关联风险。在这篇博客中,将分享一些方法和技巧,帮助商家提高Wis…

