导言:
在使用MySQL数据库的时候,我们知道了它有两种物理存储结构,hash存储和B+树存储,由于hash存储使用的少,而B+树存储使用的范围就多些,如 InnoDB和MYISAM引擎都是使用的B+树作为存储结构,
B+树,顾名思义,它还是树形结构,那么它是怎么演变过来的,那么就需要从数据结构的角度来分析了
一.顺序查找
无序线性表
在计算机发展之初,使用什么来存储数据,一般都是使用顺序存储来做的,比如链表或者数据,它们有很明显的特点就是线性结构
当一些数据存储在数组中后,每次查找都需要从前往后,或者从后往前,在算法中可以叫它蛮力法,一次一次的对比找到结果,效率十分低下

使用线性数据表搜索查询效率很不稳定,运气好的时候可能一下就找到了结果,运气不好又要找到最后,当然在小范围的查询或者临时存储是由用的
那么继续基于线性查询,我们很快就发现普通的顺序表查询是可优化的,
我们现在查询的数据都是未排序的,如果我们在插入或者说构造数据结构的时候就先排序,再按要求查询会怎么样呢?
有序线性表

这种优化以后的查找,我们称之为折半查找,在排好序的有序序列中,通过key值和当前顺序结构的中间元素对比,如果比此元素大,说明key值在后面部分,如果比此元素小,说明key值在前面部分,否则运气很好直接返回
折半查找就伴随着大量的剪枝操作,每次比较都会裁去一般的元素不用继续比较了,这样效率就高了起来,但是相对应的是我们插入数据就麻烦了,可能插入新数据都需要伴随大量的移动
其实这种思想我们早就在树结构中体现了,既然线性表中不好插入新数据,那么非线性结构能否优化这个问题呢?
二.非线性结构查找
二叉搜索树
使用树的方式查找,它天生的优势就是自带二分查找的功能,基本的树定义我们就不用介绍了,主要是基于二叉查找树的特性
它是自带折半查找,每次查找也是剪枝
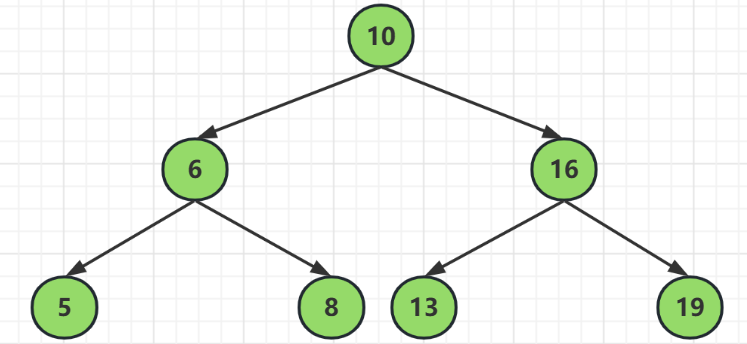
二叉查找树的特点就是以父节点为基准,总有左子树小于父节点,右子树大于父节点
我们在查找的时候和折半查找都是差不多的时间复杂度,并且每次查询都会减少一半的待比较的元素,那么二叉查找树的插入数据的效率如何呢
很显然,对于单凭数据插入,其实每个新加入的元素都能在最后一层找到自己的位置,不会有元素移动的情况
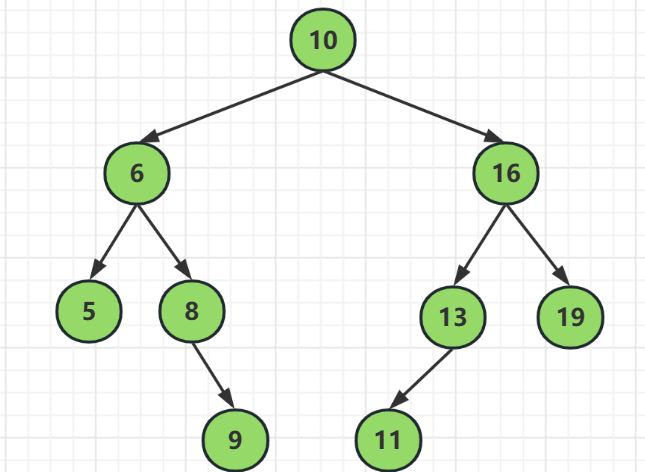
这是比较好的情况了,其实在一棵合理的树的基础上,我们进行增加数据或者删除数据是很方便的,所以二叉查找树的特性在建树的过程中序列很重要
如果一个序列的区间是连续变化很大,或者直接是递增或递减序列的时候,二叉查找树的优势就会退化成线性结构,后期新数据的插入和删除旧数据也是一样的会退化成线性结构
比如我们给定一个递增的序列:5,6,8,9,10,11,13,16,19
这个序列直接使用二叉搜索树的特性去建树会发生什么呢?
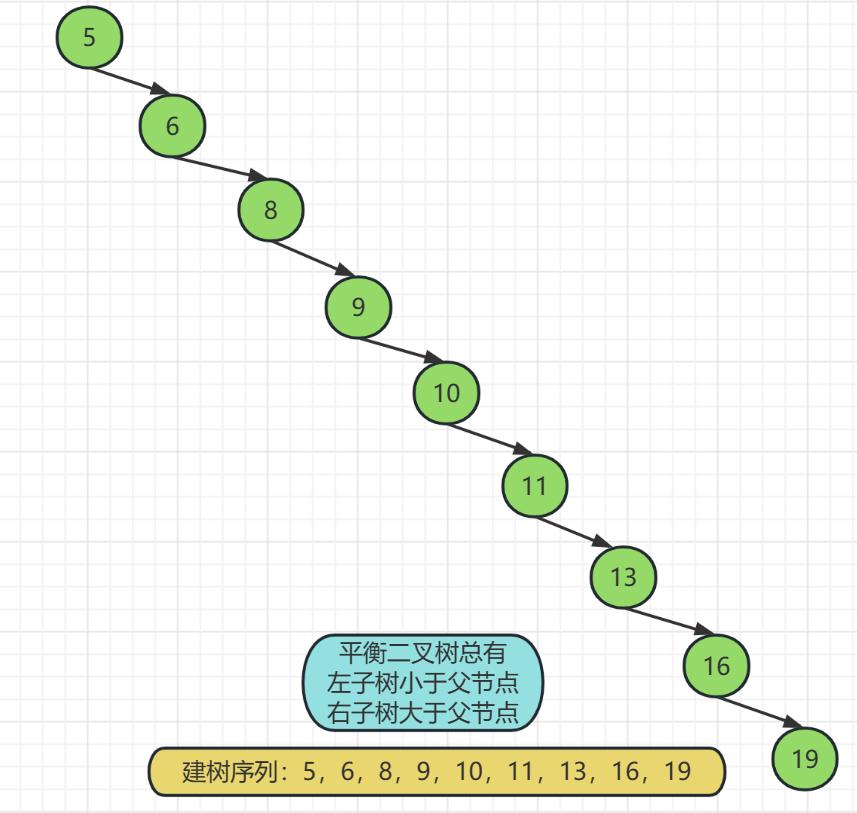
如上图,如果一个序列是连续的,使用二叉搜索树的特性直接建树是很不合理的,上面的树看起来和线性结构都是一样的,换而言之它就是一个线性结构,我们说过线性结构对于大量的插入删除操作十分不便
所以使用二叉收索树直接建树是非常不方便的,所以要更换建树的方式
平衡二叉树(AVL)
平衡二叉树是基于二叉查找树的特性,对于插入数据进行调整的
它的要求是除了要满足二叉查找树的特点,还需要满足左子树高度 – 右子树的高度 小于等于 1,也就是左右子树的层数最多相差一层,在上面的例图中,一个连续的序列导致树的右子树明显大于左子树,所以它肯定不是平衡二叉树
平衡二叉树是通过旋转得到的稳定的二叉树
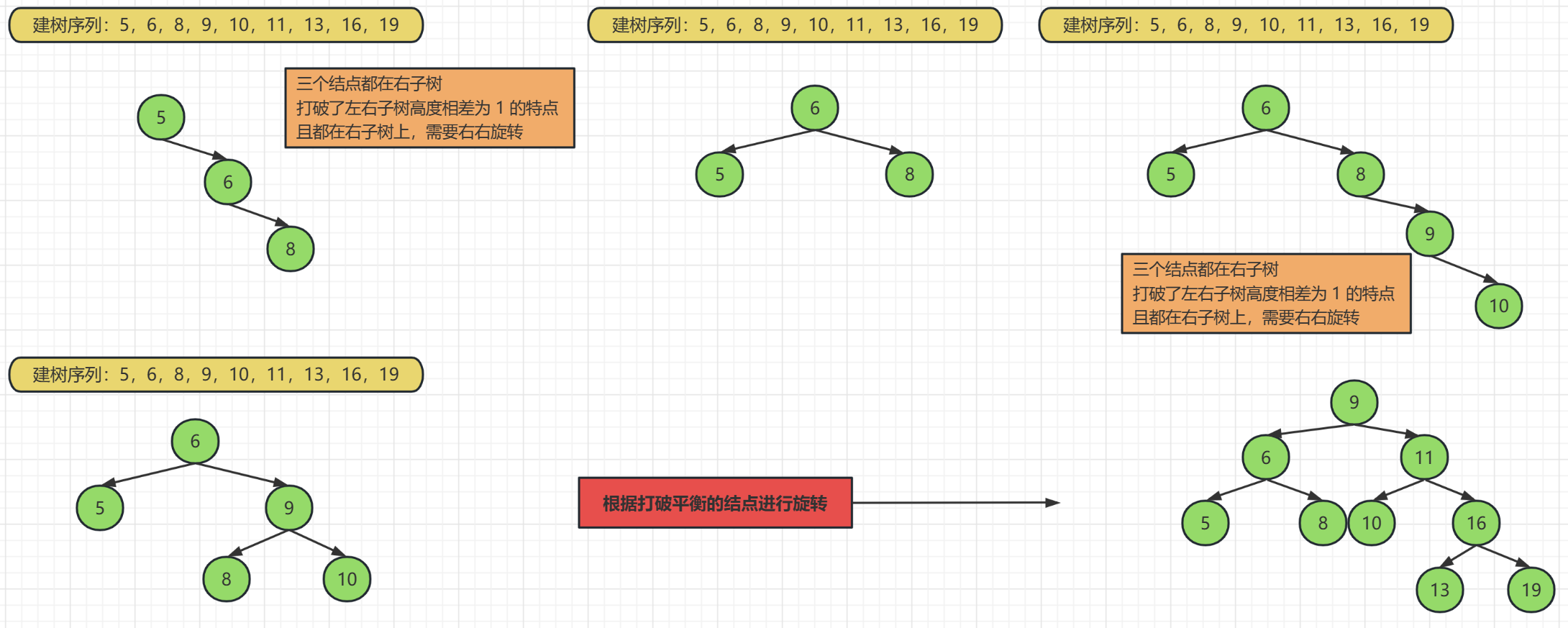
通过平衡二叉树的旋转规则,我们可以很快的构造出一棵平衡二叉树,
这样的构造方式就不存在插入新数据的时候会导致树形结构退化成线性结构的可能性了
对于平衡二叉树的旋转规则,一共有四种,可以看看我以前写的博客 二叉树补充 中有详细的介绍
当使用了平衡二叉树解决了新增数据和建树的难题,有具有二叉查找树的特性,对于小范围的查找已经不是问题了,
问题是MySQL是一个大型的数据管理系统,它内部的存储数据都是非常多的,如果说我有100个数据,交给平衡二叉树来查找,它有7层,也就是说它最坏的请款要查找7次才能找到数据
那要是10000条数据呢,就需要14层,对于14次磁盘操作是很费时间的,数据库是多人共享系统,也就是所每个人都需要14次磁盘操作,肯定是不合算的,
基于上面的分析,我们可以发现一个很明显的特征,那就是查找次数和树的层数是有关系的,如果层数低了,那么查找效率就高了
就比如我如果把100条数据为7层的树,构造成6层,5层等等,是不是查询效率就高起来了,
那么怎么优化呢?其实很简单,原来平衡二叉树不是结点只存一个元素吗?我们就要打破它,多存几个数据
这就是平衡多路查找树
B树(平衡多路查找树)
B树的是多路查找树,这就意味着其实它的结点可能不止一个元素,大多数情况都是多元素的
当多路和查找树合在在一起后我们可以知道,它满足二叉查找树的特点,也就是左子树小于根节点,右子树大于根结点
多路有表示每个结点不再存放单一的元素,而是一个有序的序列
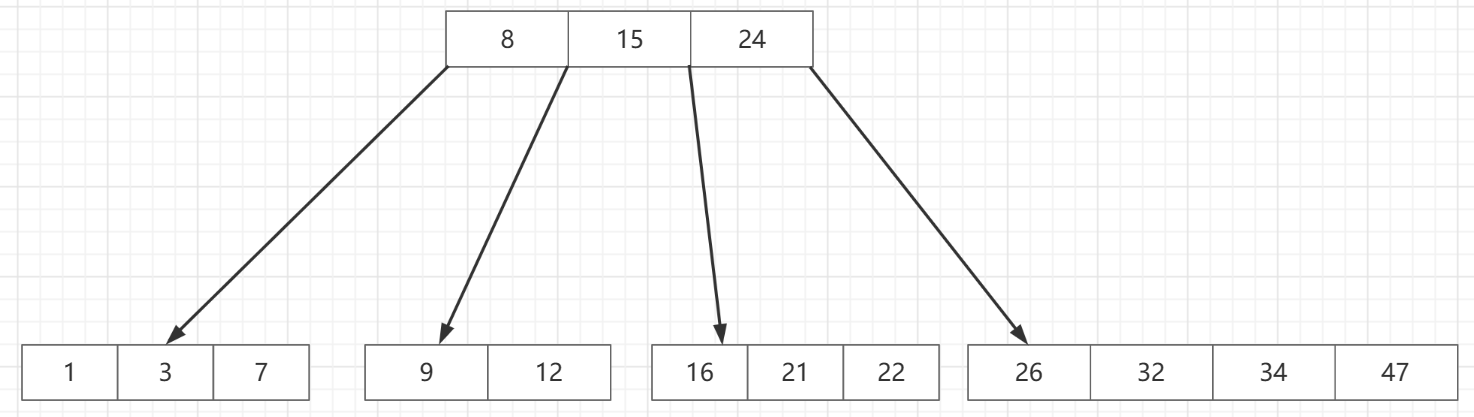
如上图,就是一棵B树,
多路,根结点到子结点有多条路可以走
查找树,始终满足左子树小于根节点,右子树大于根节点
对于B树的结点,在这里好像元素个数都是不一样的,其实这是根据234树的一个拓展,因为B树的结点都是通过上溢得来的,而每个结点插入数据不一样,上溢的次数不一样
我们可以简单的了解一下234树的上溢方式:

在B树中由于是多结点,所以上溢的地方不同,也就导致各个结点不一致
上面的描述只是介绍了基本的B树结构,其实在真正的B树存储中,它的结点是即存储索引,也存储数据的
B树的存储其实已经很优了,但是对于数据库系统来说,使用B树来做存储结构有不足,其中包括非叶子结点中即存数据又存储索引,查找不稳定,存在有些查找一次就可以拿到结果,而有些查找却需要其最底层,其中其它层都有可能,所以查找数据的频率不稳定
其二它不符合数据库的查询准则,那就是大范围查询,由于数据分布在磁盘的各个扇区内,一旦一个扇区取值没到范围,就需要重新磁头定位,十分麻烦
所以,为了符合数据库自身的特点,B+树就诞生了
B+树
B+树的其它特性都是和B树一样的,我们重点讲一下它们的不同点
B+树在非叶子结点都不在存储数据,而是都存储索引,而叶子结点都存储数据,关于B+树索引部分可以参考 MySQL存储之B+树中索引部分
这样改装以后有什么好处呢?
- 非叶子结点都存索引,索引一多,指向的数据也会变多,叶子结点的数据就会变多,整个树的树高就会变低,层数低了,查询效率就高了
- 数据都在叶子结点,所以说每次查询都需要在最底层去,不存在根节点就返回数据的情况,查询数据的稳定性就高了

B+树的第二个特特点就是在数据库查询的时候,我们有很多情况下都需要取一片连续的区域
如果使用B树来定位的话一旦在叶子结点没有取完,那么就会重新从头结点开始进行磁头定位,十分影响效率,所以在B+树中,在叶子结点的尾部增加了指针,用于指向下一片区域,用于磁头的连续取值
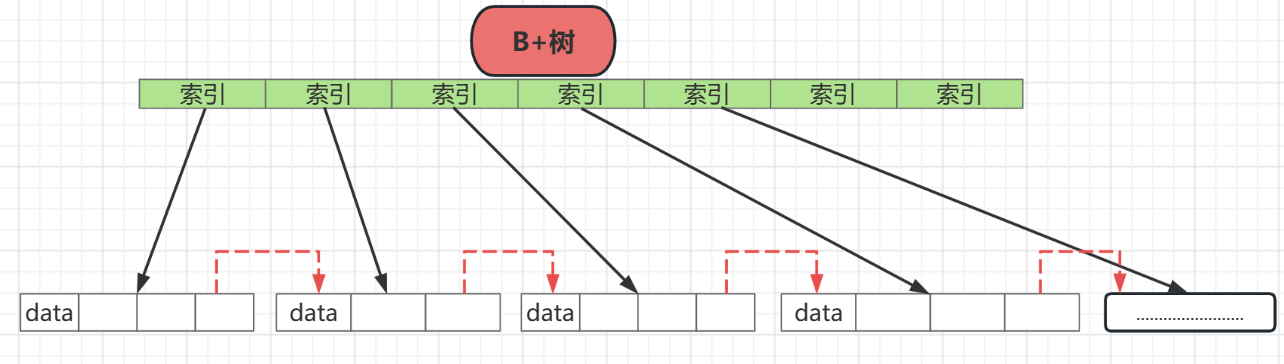
如上图,正是这些尾部指针,才能使得B+树在连续取值的时候效率高,这也贴合数据库查询操作多的特点
所以B+树的优势在于查询稳定,且连续取值效率高
至于MySQL为什么不适用红黑树而使用B+树这类问题,很重要要的一点就是查询效率
红黑树的平衡条件是左子树和右子树高度可以相差一倍,一旦数据量一多,效率就太不稳定了
但是红黑树宽泛的平衡条件,在程序运行的堆空间是很高效的,宽泛的平衡代表不需要过多的旋转
所以,各自在各自的领域有各自的优势,就目前来看B+树比红黑树更适合数据库的存储,
大家也可以去深入了解一下红黑树,我所描述的就这么多,希望学术同仁不吝赐教。
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
机房租用,北京机房租用,IDC机房托管, http://www.fwqtg.net
相关推荐: [Java 实现水平分表 2]前言:常见的策略包括:
目录 前言: 常见的策略包括: Java实现哈希分表策略是一种常见的分表策略: 配置分表策略 使用分表 插入数据需要按照分表策略将数据插入到对应的分表: 定义分表Mapper接口 插入数据 哈希算法分表涉及到的代码讲解: 分表查询讲解: IN分表策略和BETW…

