NEFU OJ Problem1485 贪吃蛇大作战题解 - 服务器托管|北京服务器租用|机房托管租用|IDC托管租用|机房机柜带宽租用-价格及费用咨询

Problem:F
Time Limit:1000ms
Memory Limit:65535K

题目

Description

贪吃蛇大家一定都玩过吧，现在宋哥也要玩这个游戏，最初的时候贪吃蛇从屏幕的左下角出发，但是有一个非常不幸的事情，就是宋哥的游戏机的左键和下键坏掉了，这意味着什么？没错！他只能操控他的蛇向右或向上走了，假设屏幕被划分为10^9*109的格子，而贪吃蛇从坐标为(1,1)的格子出发，每次操作可以从坐标为(x,y)的格子前往服务器托管网坐标为(x+1,y)或(x,y+1)的格子，在所有格子中有一些格子中有一些食物，宋哥现在想知道，他的贪吃蛇最多能吃到多少食物呢？

Input

输入的第一行包含一个数字T(19),yi(1<=xi&服务器托管网lt;=109),pi(1

Output

输出T行，第i行为第i组数据的答案。

Sample Input

2
3
1 1 1
2 2 2
3 3 3
3
1 3 1
2 2 2
3 1 3

Sample Output

6
3

Hint

Source

MGH

思路

看起来像很经典的dp问题，但是区别是点很稀疏，只有1e3的点，却有1e9*1e9的棋盘，考虑将点位置重新紧密排布, 建立一个映射将稀疏点集(S)映射到紧密点集(P’)即 (f:{P_i = (X_i,Y_i)in S}rightarrow {P’_i=(X’_i,Y’_i)in S’})使得(S’)方便使用dp。

需要保证重新排布后性质不变，分析后得知需要满足保持原本的横纵坐标的大小关系即

[forall P_i, P_jin S
left{
begin{array}{c}
x_i x_j rightarrow x’_i > x’_j\
end{array}
right.
]

[forall P_i, P_jin S
left{
begin{array}{c}
y_i y_j rightarrow y’_i > y’_j\
end{array}
right.
]

如下图所示方法，删除所有空行和空列可以实现。

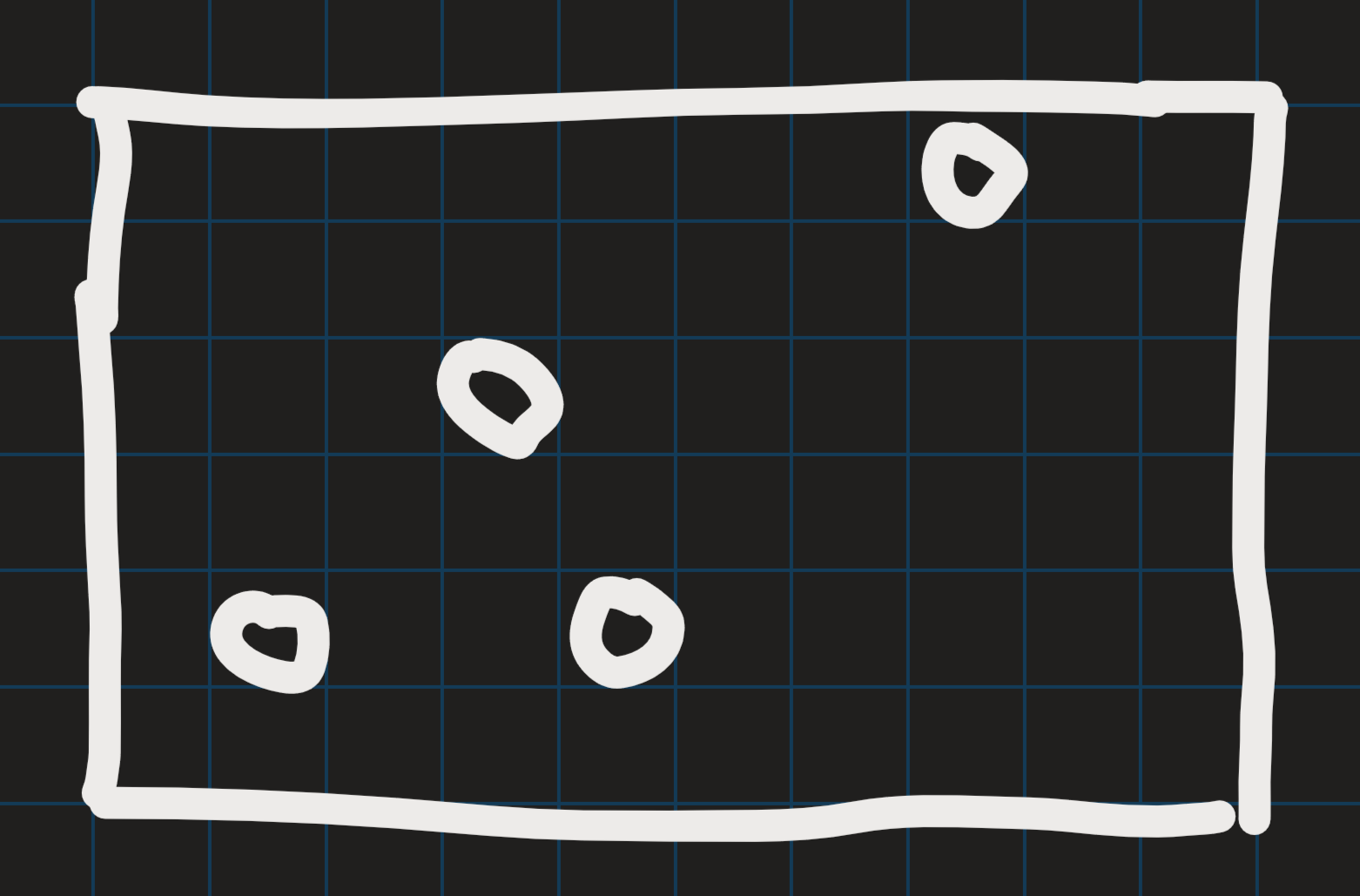
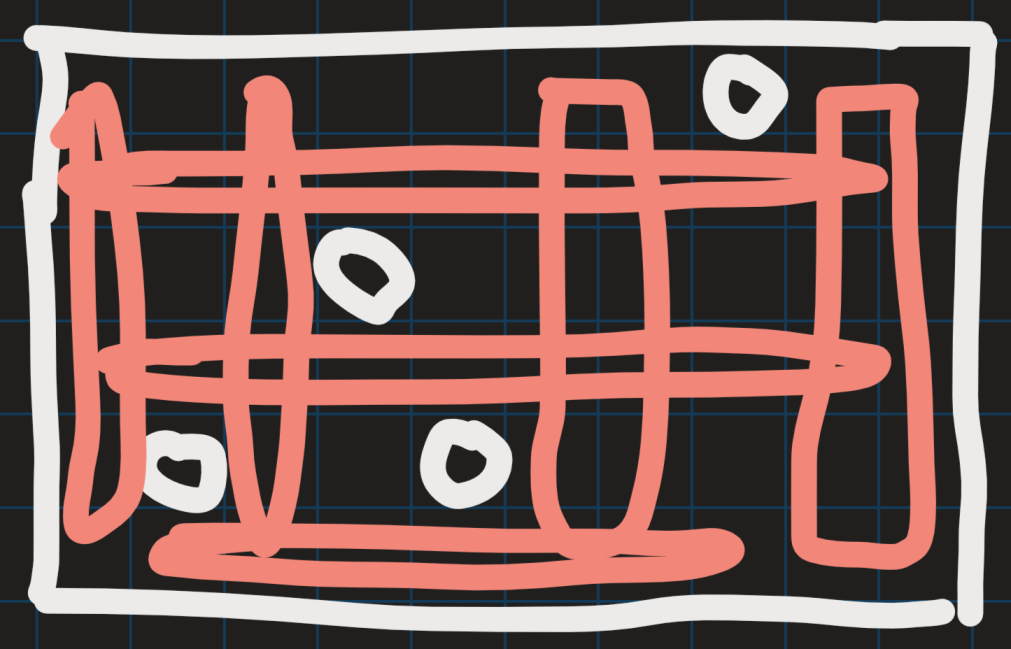
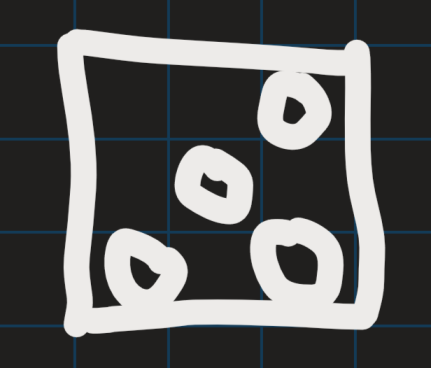
算法实现

对(x)坐标由小到大排序
对于每个点遍历从0开始分配新的(x’)坐标，如果某个点(x)坐标与上一个点相同，则分配相同的(x’)坐标，而不递增(x’)。

之后再对(y)坐标进行同样的操作。

完成后对(S’)点集进行DP即可

代码如下

#include 

using namespace std;

struct Food
{
    int x, y, v, _x, _y;//_x和_y代表映射后坐标
} food[1020];

int mp[1020][1020], dp[1020][1020];

bool Cmp1(Food f1, Food f2)//x排序
{
    return f1.x = 0)
        res = max(res, Find(x-1,y));
    if(y-1 >= 0)
        res = max(res, Find(x,y-1));
    return dp[x][y] = res + mp[x][y];
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        int n;
        cin >> n;
        for (int i = 0; i

服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.fwqtg.net

题目