本篇为RSA进阶篇，继RSA入门
[RSA3]P1（扩展欧几里得）
题目
from Crypto.Util.number import *
flag = b'******'
m1 = bytes_to_long(flag[:len(flag)//2])
m2 = bytes_to_long(flag[len(flag)//2:])
assert 18608629446895353521310408885845687520013234781800558*m1-14258810472138345414555137649316815272478951117940067*m2 == 1我的解答：
本题非常直白，将flag分成两部分后给了一个约束式，让我们求解flag。
约束是一个二元一次方程，显然我们知道二元一次方程在实数域上会有无数个解，但注意我们很少会在实数域上进行运算，如之前所说，我们所有的操作都是在一个整数域或者有限域（可以理解为取模的域）中进行运算。而这里我们便有一个非常常用的裴蜀定理
裴蜀定理：对于整数域中的不定方程 ax + by = m 其有解的充要条件为gcd(a,b)∣m
显然我们可以计算发现题目中约束的两个值其最大公因数为1，所以我们是可以算出未知数的，我们可以利用扩展欧几里得算法进行该约束方程
import gmpy2
from Crypto.Util.number import *
a = 18608629446895353521310408885845687520013234781800558
b = 14258810472138345414555137649316815272478951117940067
print(gmpy2.gcd(a,b))
#1之前我们都是将extgcd作为黑盒来进行使用，现在我们便要学习其原理，而要明白扩展欧几里得我们则需要先了解欧几里得算法，即用来求解最大公因数的辗转相除法
def gcd(a, b):
return a if b == 0 else gcd(b, a%b)举个例子：a=2 b=1 如果b==0那么返回a否则一直返回gcd()函数辗转下去直到b==0。 其实2和1的最大公因数是1 因此a%b=0 b=1 返回gcd(1,0)再次带入函数满足if b==0 因此返回1即为所求。就这么个意思。。也是很好理解。
以上是欧几里得算法的一个Python实现，其原理利用了递归的思想，这是编程中常用的一种思想手段
- 设立一个边界值。
- 设立递归量，并且不断的归约。
递归的本质思想还是归约，即把一个问题转化为另一个较简单的问题，如果那个较简单的问题还是问题本身则我们就可以称为递归，在这里边界条件是gcd(a, 0) = a，而归约过程则是当不为边界值时，设最大共因数为g，并设a>b此时有
a=k1b+r1
则可以将问题转化为gcd(b, a%b)，即
a=b
b=r1
因为g∣b,g∣a，则有r1/g=a/g−k1b/g，即说明r1/g是整数，有g∣r1，到这里我们证明了b,a%b的最大公因数还是g，也就说明了计算gcd(a,b)和计算gcd(b,a%b)等价，所以我们便可以按照此方式不断的进行归约最终直到到达边界值即r1=0时，则说明此时的b就是原式的最大公因数。
现在来考虑扩展欧几里得，在刚才我们所说的边界值(a=g,b=0)时有
a⋅1+b⋅0=gcd(a,b)
即此时解为x=1,y=0，这同样也是扩欧的边界条件，那么我们从边界值往回看代入上面我们所述的等价关系中可以得到
ax1+by1=gcd(a,b)
b⋅x2+(a%b)y2=gcd(b,a%b)
那么现在我们要做的就是寻找这两个式子中的转移关系，从而找到x1和x2的联系，y1和y2的联系，从而和欧几里得一样写出转移式便可以得到完整实现了。
我们知道a mod b=a−(a/b)b，代入上述关系中则有
g=bx2+(a−(a/b)b)y2
=bx2+ay2−(a/b)by2
=ay2+b(x2−(a/b)y2)
显然我们便得到了关系式
x1=y2
y1=x2−(a/b)y2
代码实现为
def extgcd(a, b):
if b == 0:
return a, 1, 0
g, x, y = extgcd(b, a%b)
return g, y, x - (a//b)*y本文大费篇幅的讲解扩展欧几里得的作用是希望大家能了解这种编程思维，了解其算法的本质，随着学习越来越深，我们会发现很多问题都是通过找到其关系式归约成较为简单的问题进行计算，而计算的核心便是边界条件和转移方程。
后面的过程便很简单了，我们通过extgcd直接求解即可。不过这里还有个值得注意的是你会发现得到的值不是flag，因为(x+kb,y+ka)依然是原方程的解，所以我们得到的只是一组解，后续我们可以通过遍历的手段找到我们想要的那一组即可。
exp:
from Crypto.Util.number import *
def extgcd(a, b):
if b == 0:
return a, 1, 0
g, x, y = extgcd(b, a%b)
return g, y, x - (a//b)*y
solve = extgcd(18608629446895353521310408885845687520013234781800558,14258810472138345414555137649316815272478951117940067)
a = abs(solve[1])
b = abs(solve[2])
for _ in range(10):
b += 18608629446895353521310408885845687520013234781800558
a += 14258810472138345414555137649316815272478951117940067
if b'NSSCTF' in long_to_bytes(a):
print(long_to_bytes(a)+long_to_bytes(b))
break
#NSSCTF{4cdc3370-b5db-4f88-bd95-a43d232a9af9}[RSA3]P2（高次Rabin）
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
p = getPrime(256)
q = getPrime(256)
assert p%4 == 3 and q%4 == 3
n = p*q
e = 4
m = bytes_to_long(flag)
c = powmod(m, e, n)
print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')
'''
p = 59146104467364373868799971411233588834178779836823785905639649355194168174467
q = 78458230412463183024731868185916348923227701568297699614451375213784918571587
e = 4
c = 1203393285445255679455330581174083350744414151272999693874069337386260499408999133487149585390696161509841251500970131235102423165932460197848215104528310
'''我的解答：
本题是Rabin攻击的进阶题目，e从普通Rabin攻击中的2变成了4
其实很简单，我们要的是e=2，那么就把m4看成(m2)2即可，然后我们需要解两次Rabin一共会得到16组解，当然这里面只有一组解是我们想要的
from Crypto.Util.number import *
p = 59146104467364373868799971411233588834178779836823785905639649355194168174467
q = 78458230412463183024731868185916348923227701568297699614451375213784918571587
e = 4
c = 1203393285445255679455330581174083350744414151272999693874069337386260499408999133487149585390696161509841251500970131235102423165932460197848215104528310
n = p*q
def rabin(c):
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
yp = inverse(p,q)
yq = inverse(q,p)
r = (yp * p * mq + yq * q * mp) % n
r_ = n - r
s = (yp * p * mq - yq * q * mp) % n
s_ = n - s
return r,r_,s,s_
c_list = rabin(c)
for c in c_list:
cc = rabin(c)
for c in cc:
flag = long_to_bytes(c)
if b'NSSCTF' in flag:
print(flag)完成本题后考虑完成[NSSRound#11 Basic]ez_signin，本题的e更大，需要更多次Rabin，但其思想依然一样，一层一层的剥开即可，主要是考察代码编写能力，再两层时我们可以手动两次rabin，但多层时则需要考虑将重复的过程变成循环调用。
练习题附件：
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
assert p > q
n = p*q
e = 65536
m = bytes_to_long(flag)
num1 = (pow(p,e,n)-pow(q,e,n)) % n
num2 = pow(p-q,e,n)
c = pow(m,e,n)
print("num1=",num1)
print("num2=",num2)
print("n=",n)
print("c=",c)我的解答：
看代码我们来分析一下：
num1 = pe – qe mod n
num2 = (p-q)e mod n
展开二项式，可消除有关pq的式子得到：
num2 = pe + qe mod n
num1 + num2可得：
num1 + num2 = 2 * pe mod n
可知num1 + num2与n存在最大公约数p，即
p = gmpy2.gcd(num1 + num2, n) q = n // p
根据上述信息可求出p，而我们还发现e = 65536 = 216 看看是否满足罗宾算法（p和q分别对4求余都余3），我们先打印出p和q，连接靶机获取数据
from Crypto.Util.number import *
import gmpy2
num1= 59840554996025694197419837189299767141940919715083637654590543115482567229570169968180333006737083033173640866902902364360226289191009120560048572276043297679698270018763241430670630221816123229643718524930305733411995058321246483012416783450164505404278181286375702214782638882589215047041540643751820438650
num2= 70301070373634513926049524952229729017142862474697524234482038124399214326930000632015602808726712181546092289090230189591723263274465552548769021531533175648839430913528523763760597918547982074144314182823302433073954446756980384446970832874273337024068865548607438142897707361226641950883893016125627317925
n= 83259153787408481802298172628070538063180243279118822048895436129104646961832489700344990509641075437593032619810941629193033330438750693874646304836611824526477669709259763560237509463402912800036782645033069044253256413587810472745029639201991765028462888276108946164222702893043130223954537803720769813961
c= 58268127136484324736541152689050543502588381405979475157975221269010580661696065122756953881557554545000538254945151815327795117708948096914509260945996365333557981515911235515197880724674416027760147441440391678566669385473579785994196434388385255047471922757636404487092029602174375073292006920000880956054
p = gmpy2.gcd(num1+num2,n)
q = n//p
print(p)
print(q)
p = 11163366577405559823179946410328743608623660246099475332229857780096673033301409127248470264100525259289819163831489656616010705381426665456453385258652459
q = 7458247761559977316768147289656358304802701515829268324407017064749170626211829946444531012079347474791382886095795760284151293736859044682373662227548379
pp = p%4
qq = q%4
print(pp)
print(qq)
#3
#3可以看出余数都是3，p和q都属于4k+3型素数。因此就好办了，直接16次罗宾算法即可
exp:
from Crypto.Util.number import *
import gmpy2
num1= 59840554996025694197419837189299767141940919715083637654590543115482567229570169968180333006737083033173640866902902364360226289191009120560048572276043297679698270018763241430670630221816123229643718524930305733411995058321246483012416783450164505404278181286375702214782638882589215047041540643751820438650
num2= 70301070373634513926049524952229729017142862474697524234482038124399214326930000632015602808726712181546092289090230189591723263274465552548769021531533175648839430913528523763760597918547982074144314182823302433073954446756980384446970832874273337024068865548607438142897707361226641950883893016125627317925
n= 83259153787408481802298172628070538063180243279118822048895436129104646961832489700344990509641075437593032619810941629193033330438750693874646304836611824526477669709259763560237509463402912800036782645033069044253256413587810472745029639201991765028462888276108946164222702893043130223954537803720769813961
c= 58268127136484324736541152689050543502588381405979475157975221269010580661696065122756953881557554545000538254945151815327795117708948096914509260945996365333557981515911235515197880724674416027760147441440391678566669385473579785994196434388385255047471922757636404487092029602174375073292006920000880956054
p = gmpy2.gcd(num1+num2,n)
q = n//p
#print(p)
#print(q)
#p = 11163366577405559823179946410328743608623660246099475332229857780096673033301409127248470264100525259289819163831489656616010705381426665456453385258652459
#q = 7458247761559977316768147289656358304802701515829268324407017064749170626211829946444531012079347474791382886095795760284151293736859044682373662227548379
#pp = p%4
#qq = q%4
#print(pp)
#print(qq)
#3
#3
p = 11163366577405559823179946410328743608623660246099475332229857780096673033301409127248470264100525259289819163831489656616010705381426665456453385258652459
q = 7458247761559977316768147289656358304802701515829268324407017064749170626211829946444531012079347474791382886095795760284151293736859044682373662227548379
e = 65536
c = 58268127136484324736541152689050543502588381405979475157975221269010580661696065122756953881557554545000538254945151815327795117708948096914509260945996365333557981515911235515197880724674416027760147441440391678566669385473579785994196434388385255047471922757636404487092029602174375073292006920000880956054
n = p*q
def rabin(c):
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
yp = inverse(p,q)
yq = inverse(q,p)
r = (yp * p * mq + yq * q * mp) % n
r_ = n - r
s = (yp * p * mq - yq * q * mp) % n
s_ = n - s
return r,r_,s,s_
cs = [c] #把c放入列表里面
#[58268127136484324736541152689050543502588381405979475157975221269010580661696065122756953881557554545000538254945151815327795117708948096914509260945996365333557981515911235515197880724674416027760147441440391678566669385473579785994196434388385255047471922757636404487092029602174375073292006920000880956054]
#循环16次罗宾算法
for i in range(16):
ps = [] #设置一个空列表用来存放最后结果
for c2 in cs:
r,r_,s,s_ = rabin(c2)
if r not in ps:
ps.append(r)
if r_ not in ps:
ps.append(r_)
if s not in ps:
ps.append(s)
if s_ not in ps:
ps.append(s_)
# print(ps)
cs = ps
for i in range(len(cs)):
print(long_to_bytes(cs[i]))
#NSSCTF{ec79d1a7-edf4-4814-8404-de681b8358db}[RSA3]P3（连分数利用）
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
m1 = bytes_to_long(flag[:len(flag)//2])
m2 = bytes_to_long(flag[len(flag)//2:])
p1 = getPrime(1024)
p2 = next_prime(p1)
q1 = getPrime(400)
q2 = getPrime(400)
n1 = p1 * p1 * q1
n2 = p2 * p2 * q2
e1 = getPrime(128)
e2 = getPrime(128)
c1 = pow(m1, e1, n1)
c2 = pow(m2, e2, n2)
print(f'n1 = {n1}')
print(f'e1 = {e1}')
print(f'c1 = {c1}')
print(f'n2 = {n2}')
print(f'e2 = {e2}')
print(f'c2 = {c2}')
'''
n1 = 45965238261145848306223556876775641787109249067253988455950651872774381183888979035386577960806305813634216583223483001245996467366520071511779063266315692543617195166613592991812117446772937889819643718423377609566597230873623011099295202599905646652692946273375405832062164263711151844949794774229886016858313299259387152937467743637367261734624060321171598033647661809876890249035267180368762739600552966699295210431508056693524383116052539072065535970720901196322942269916455391238409489616842687658335666652878840458263998780783865062993401055465701207886230787204008073260653659510197069116237460322442433331870944968133645513020531983926180514313028320422449103156746225574626841023639595418255472716267486241462968101152032898749
e1 = 279586443815379026299414729432860797623
c1 = 11515318475856179010858377918435934663304239594599788732135470038988222237790835017056954077794506499559722814863240838882673078330335616745578747265404229105473136943188301293198548838105990504750972653445744347121859396823995101611868191609259910876207038154174100742978387355304521374228562928260479446249263909934393657537918407756957032700052269827171045167752168509783885071211516601218892308228572735545579606908430615218499620619028799140945676768341492724044499209913045110359935325510223652935426973411960865908064824205626343685369866932545651037748553442488682593143020861196339307665638704485958986411837014559504992818255506454051842453553265179370878637153602580071152915165775491633322055360737581203750897698007951117808
n2 = 25459365600568360055376316722846535809281537088824978187355135247184417413329012865221456308642116409716822227032113740366024809533942721286337697830775221199570509665320400376959076685728357107457862901087218522281771857981155239522807950207375964963527837592797198372303427082343684305143238075402697262610809363109748984974325271762535573995993132076293275456692621516174749076897962348000698039074721998780555541905706268579496243099763776676950336105074846695227221690550755501320117554250942600626927600558489780841103863110357615957088709321079080707735028039675102383525496673233697130053936053431067133520717494376952763684807635780416860233261892013531534059267366382617635000415723745274490604551078385404286689447761642713963
e2 = 249615977162294580923494787210301891647
c2 = 24544357952213952357056140974408354173440635791397720610932999473703241918398814255275362994811954064820912468224131892551724930677715676493892869921426790840199600798807085779112854131346378899855545138289836687048918660685766286852276199524789699567994154833159365800848535248059731927121269157841084905465048764152977389352561685340108834453730139893330210765986258703154334901509553990091592209268471594519326651914685843021165854654380119091009831071244459145750976193183411590207529489774630266528538380011000213950174694472355034075543687572037516433204151217601537869823709241020510051494619335852686100897182065588340025334679570763716458250649152257797833022586793526594784648938165537701256313728194521212887453997160504204832
'''我的解答：
本题给了两组公钥和密文，之前我们学习过多组公钥时可以考虑共享素数，但从代码上来看可以发现他们使用的都是不一样的素数，但我们又会发现这些素数之间并不是完全独立的。
p2是p1的下一个素数，或者换种说法说，他们离得非常近，在考虑一下我们曾经所学过的攻击关于非常近的无外乎是p-q过小，我们可以利用费马分解进行操作，但这里两个非常近的素数并没有进行乘积，而是分开和其他数进行乘积。还有一种情况便是维纳攻击，在维纳攻击中我们说是当e和n非常接近时便可以使用，那这里和维纳攻击有什么关系呢？
实际上我们这里将要了解维纳攻击的核心：连分数定理
连分数定理：当a和b满足
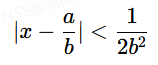
时，则a/b是x的一个连分数近似。
连分数近似则代表我们可以对x进行连分数展开，其中的某个近似数便是a/b。
本定理便是我们的理论支撑，那么现在我们有了两个很近的数n1和n2，如果我们对这两个数进行连分数展开，我们的预期结果便是可以在展开的过程中得到p1和p2。当然我们现在还无法判断他们之间的关系是否符合上式，我们只能先进行展开，随后进行验证
from Crypto.Util import number
import gmpy2
n1 = 45965238261145848306223556876775641787109249067253988455950651872774381183888979035386577960806305813634216583223483001245996467366520071511779063266315692543617195166613592991812117446772937889819643718423377609566597230873623011099295202599905646652692946273375405832062164263711151844949794774229886016858313299259387152937467743637367261734624060321171598033647661809876890249035267180368762739600552966699295210431508056693524383116052539072065535970720901196322942269916455391238409489616842687658335666652878840458263998780783865062993401055465701207886230787204008073260653659510197069116237460322442433331870944968133645513020531983926180514313028320422449103156746225574626841023639595418255472716267486241462968101152032898749
e1 = 279586443815379026299414729432860797623
c1 = 11515318475856179010858377918435934663304239594599788732135470038988222237790835017056954077794506499559722814863240838882673078330335616745578747265404229105473136943188301293198548838105990504750972653445744347121859396823995101611868191609259910876207038154174100742978387355304521374228562928260479446249263909934393657537918407756957032700052269827171045167752168509783885071211516601218892308228572735545579606908430615218499620619028799140945676768341492724044499209913045110359935325510223652935426973411960865908064824205626343685369866932545651037748553442488682593143020861196339307665638704485958986411837014559504992818255506454051842453553265179370878637153602580071152915165775491633322055360737581203750897698007951117808
n2 = 25459365600568360055376316722846535809281537088824978187355135247184417413329012865221456308642116409716822227032113740366024809533942721286337697830775221199570509665320400376959076685728357107457862901087218522281771857981155239522807950207375964963527837592797198372303427082343684305143238075402697262610809363109748984974325271762535573995993132076293275456692621516174749076897962348000698039074721998780555541905706268579496243099763776676950336105074846695227221690550755501320117554250942600626927600558489780841103863110357615957088709321079080707735028039675102383525496673233697130053936053431067133520717494376952763684807635780416860233261892013531534059267366382617635000415723745274490604551078385404286689447761642713963
e2 = 249615977162294580923494787210301891647
c2 = 24544357952213952357056140974408354173440635791397720610932999473703241918398814255275362994811954064820912468224131892551724930677715676493892869921426790840199600798807085779112854131346378899855545138289836687048918660685766286852276199524789699567994154833159365800848535248059731927121269157841084905465048764152977389352561685340108834453730139893330210765986258703154334901509553990091592209268471594519326651914685843021165854654380119091009831071244459145750976193183411590207529489774630266528538380011000213950174694472355034075543687572037516433204151217601537869823709241020510051494619335852686100897182065588340025334679570763716458250649152257797833022586793526594784648938165537701256313728194521212887453997160504204832
def continuedFra(x, y):
cF = []
while y:
cF += [x // y]
x, y = y, x % y
return cF
def Simplify(ctnf):
numerator = 0
denominator = 1
for x in ctnf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return (numerator, denominator)
def getit(c):
cf = []
for i in range(1, len(c)):
cf.append(Simplify(c[:i]))
return cf
def attack(e, n):
cf = continuedFra(e, n)
for (p2, p1) in getit(cf):
if p1 == 0:
continue
if n1 % p1 == 0 and p1 != 1:
return p1, p2
print('not find!')
q1, q2 = attack(n1, n2)
p1 = gmpy2.iroot(n1//q1, 2)[0]
p2 = gmpy2.iroot(n2//q2, 2)[0]
phi1 = p1*(p1-1)*(q1-1)
phi2 = p2*(p2-1)*(q2-1)
d1 = gmpy2.invert(e1, phi1)
d2 = gmpy2.invert(e2, phi2)
m1 = number.long_to_bytes(gmpy2.powmod(c1, d1, n1))
m2 = number.long_to_bytes(gmpy2.powmod(c2, d2, n2))
print(m1+m2)
#NSSCTF{ee5cb1a5-257a-48b0-9d62-9ef56ff0651a}上面是完整的WP，在中间我们可以插入一行
assert n1/n2 - q1/q2
会发现他也是显然满足的。
连分数展开之后的内容便是常规RSA界面操作，不在赘述。
这里我们可以发现，只要发现题目中有差不多大的数，便可以寻找是否还有另外两个差不多大的数，并且这些数之间都是有联系的，只要能够找到这样的关系我们便可以考虑对较大的两个数进行连分数展开得到近似数，便有可能得到想要的值。
[RSA3]P4（连分数进阶）
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'******'
flag = bytes_to_long(flag)
p = getPrime(1024)
r = getPrime(175)
a = inverse(r, p)
a = (a*flag) % p
print(f'a = {a}')
print(f'p = {p}')
'''
a = 79047880584807269054505204752966875903807058486141783766561521134845058071995038638934174701175782152417081883728635655442964823110171015637136681101856684888576194849310180873104729087883030291173114003115983405311162152717385429179852150760696213217464522070759438318396222163013306629318041233934326478247
p = 90596199661954314748094754376367411728681431234103196427120607507149461190520498120433570647077910673128371876546100672985278698226714483847201363857703757534255187784953078548908192496602029047268538065300238964884068500561488409356401505220814317044301436585177722826939067622852763442884505234084274439591
'''我的解答：
上一题理解之后再看这一题就简单很多了
我们把代码中的式子捋一捋
mr−1 ≡ a (mod p)
现在我们已知a和p，求解m，咦我们会发现这和之前说的不一样啊，虽然a和p很接近，但是哪里存在另外两个数呢？
我们将上面的式子变变形状，从有限域（取模的整数域）变成实数域
m = ar + kp
则有
m/rp – a/p = k/r
因为m相对于rp来说是一个非常小的数，所以我们得到近似关系
a/p ≈ k/r
找到了近似关系后，后面的做法便很简单了，展开后得到(r,k)，就可以进一步求解m了。
exp:
from Crypto.Util.number import *
import gmpy2
a = 79047880584807269054505204752966875903807058486141783766561521134845058071995038638934174701175782152417081883728635655442964823110171015637136681101856684888576194849310180873104729087883030291173114003115983405311162152717385429179852150760696213217464522070759438318396222163013306629318041233934326478247
p = 90596199661954314748094754376367411728681431234103196427120607507149461190520498120433570647077910673128371876546100672985278698226714483847201363857703757534255187784953078548908192496602029047268538065300238964884068500561488409356401505220814317044301436585177722826939067622852763442884505234084274439591
def continuedFra(x, y):
cF = []
while y:
cF += [x // y]
x, y = y, x % y
return cF
def Simplify(ctnf):
numerator = 0
denominator = 1
for x in ctnf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return (numerator, denominator)
def getit(c):
cf = []
for i in range(1, len(c)):
cf.append(Simplify(c[:i]))
return cf
cf = continuedFra(a, p)
for (r, k) in getit(cf):
if r == 0:
continue
y = abs(a*r - k*p)
flag = long_to_bytes(y)
if b'NSS' in flag:
print(flag)
#NSSCTF{e572546b-abb5-4358-8970-471abc12b7ef}其实我们也可以发现真实比赛时，看到近似值可以先不用找具体的关系，展开就对了，再假定展开得到的值就是某个需要的值进行进一步计算，一般都是可以得到结果的：）
实际上本题可以用格密码转化成SVP进行求解.
[RSA3]P5（再探CRT）
题目
from Crypto.Util.number import *
from gmpy2 import *
import random
flag = b'******'
flag = bytes_to_long(flag)
nl = []
cl = []
def getn(bits):
n = 1
while n.bit_length() 我的解答：
本题依然还是一个广播攻击的题目
我们知道广播攻击就是给了多组同余方程，我们利用中国剩余定理CRT便可以得到通解，但是在本题直接套用之前的exp你会发现报错了，你会得到提示逆元不存在，这便是本题的考点，不互素的CRT。
回顾CRT我们有：
我们发现这里面是需要求解逆元得到ti的，当我们遇到不互素即
gcd(ni,nj)≠1
时，实际上我们有一种朴素的做法，设gcd(ni,nj)=g
则
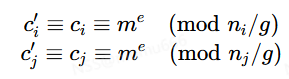
这样我们便得到了两个新的同余方程，并且他们的模(ni/g,nj/g)是互素的，这种做法是没有问题的但多组模数互相包含多个因子时，这种做法便变得非常繁琐，因为只得到上述式子的话实际上是丢失信息的，你还需要得到对于pi∣g的每个同余式
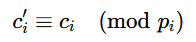
这样得到的所有式子做CRT才能够得到足够多的有效值。
-
因为只得到上述式子的话实际上是丢失信息的，你还需要得到对于pi∣g的每个同余式，关于上面这句的含义可以自行用具体值进行测试理解，有很多内容如果将其展开的非常平坦的话会显得非常的枯燥，所以希望大家能够自己动手来理解一些内容，这比看一百遍资料还要有效。对于足够多实际上就是能够得到原始值就是足够多，得不到便是不够多，这也是本题为什么给了8组而不是7组的原因，因为不互素的因子会产生一些无效信息，比如补充其他额外信息才能够得到有效的信息。
-
那么我们介绍了朴素的方案之后我们希望寻找一种和CRT一样的通解手段而不是预处理，这里我们先考虑两个方程的情况
其中gcd(n1,n2)=g=1，则有
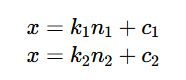
即k1n1+c1=k2n2+c2，移项得到
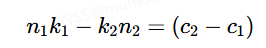
我们现在要应该对这个式子非常眼熟，此等式成立则说明gcd(n1,n2)∣(c2−c1)(翡镯定理)，则有
即
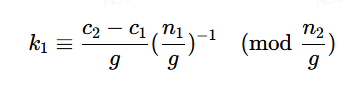
有
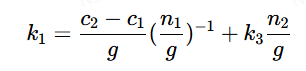
代入最初和x的式子得
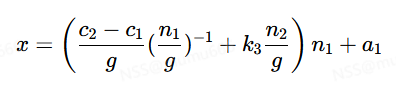
整理得
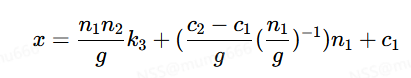
即
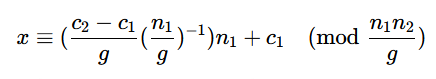
这样我们便合并了两个模不互素的同余式得到了一个方程。
部分同学可能会看的迷迷糊糊，我这里总结两个可能会看不懂的点
1.绕来绕去是在干嘛？为什么不直接用k1，k2
我们知道k1,k2包括k3都是存在的，但是我们求不出它们来（能求出来就直接得到x了），所以我们必须通过已知值来进行替换。
2.
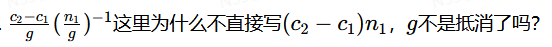
这个问题大家可能会经常犯错，在实数运算中我们确实可以这样做，但是这里要注意如果整个运算过程都是在同余的情况下我们确实可以进行抵消，但是实际上我们进行逆元的操作时的模是n2/g，而最后的模是n1n2/g，所以实际上这里是
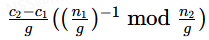
是不能够直接进行抵消的。在其他地方涉及逆元运算时也一定要小心模数是否改变。
有了这层关系之后我们便可以将上式和n3操作进行转化，最终得到一个包含所有模数的通式，余数便是我们所需的原始值。
实际上上述过程也就是CRT的操作过程，只是我们在运算过程中进行了除g的操作，使得计算过程中的逆元是存在的。
其实CRT的本质就是利用同余式
而这里我们便可以通过扩展欧几里得进行求解，因为上式本质便是
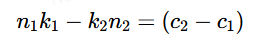
最后得到k1,k2从而得到一个解x0，只是因为取模导致我们得到的是
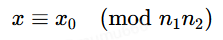
最终我们凑齐足够多的ni得到
如果xi，则 x0便是原始值x。这便是CRT的本质运算。现在你应该知道为什么我们在P1中花了很大的篇幅来介绍扩欧和归约的思想，因为它们应用的非常广泛，很多定理及推广中都有它们的身影或思想。
exp:
from Crypto.Util.number import *
from gmpy2 import *
nl = [48900330639594979739701067783234903348599405413588466525574910520196852415104874636276388006189258357683981763, 52184798260918956005878710130354843122927544013692595240956998112200987084814453592388074200951779840156511, 57591305346419909943538345276263585821186563609432856462492112562586368230163591993342956384688555395772999, 1391052858660682537388264601016075339528373211889618359237336378385137832855656756800539626220549334300176727, 8401669052993451281764489325068020625937224410830694438332016050030698435746929661939302694116817188225591, 66809775375777747860816961274643428927028556487820183599747024350362932190079439298182707730302976119988715497, 41209230281867957743385705727577318625405890894626062454495908709761427062490881938652489884059847194603237277, 31140089821370202352241944402736292072447365626312703496944186462246895695650729682254970622208848300946861]
cl = [26617913696414745819584063604277199673357890677059949687794606743781436349829925794253672010780125661705587071, 6332739614121961923948917957498597962902897015582697635859365080803944882904908423983706426654363433337197, 46154051334276357655176765655327305918368830821288083739892570534253190653909520953027859629573215723954424, 2800905135165447908315158053695706832127646195243072751493365013371469263897970241141686022109978485359114, 3597083928897756955519089479028751799504001377334447013725903377254761160933418420625119547713455139382114, 17032086144873551648611964054579542303630306316746409528107026138674853298939194425805809444921339677455174485, 36111201824253386572496248461433786832561483450731317363761227351689971628309683994429845284904292821369745345, 28548175317543234723297895187238113463350377151401226415566179373530461612253257137535830491771909906093171]
def excrt(m, r):
lcm = m[0]
R = r[0]
for i in range(1, len(m)):
d, x, y = gcdext(lcm, m[i])
c = R - r[i]
if c % d:
return -1
x = x * c // d % (m[i] // d)
R -= lcm * x
lcm = lcm * m[i] // d
R %= lcm
return (R + lcm) % lcm
m = excrt(nl, cl)
print(m.bit_length()//7)
print(long_to_bytes(iroot(m, 7)[0]))
#NSSCTF{6ff0651a-48b0-257a-9d62-9ef5ee5cb1a5}[RSA3]P6（限定范围的p-1）
题目
from Crypto.Util.number import *
import random
primes = []
for i in range(1000):
primes.append(getPrime(64))
def getMyPrime(nbits: int):
while True:
n = 2
while n.bit_length() 我的解答：
本题属于P-1光滑攻击得进阶题型之一，这里我们很容易发现P是从primes里面随机选取一些素数相乘后得到的，对于传统的光滑攻击我们的做法是不断的执行
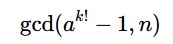
直到k!覆盖了p-1下的所有素因子为止，但这里我们发现primes里面的素数都是64位的，从1开始遍历很显然需要很长很长的时间才能覆盖，所以我们直接套用之前的脚本是不能得到答案的。
刚才我们说了在P-1光滑攻击中我们要做的就是得到一个可以覆盖所有素因子的数，显然在这里我们已经知道了P-1是由这些素数构成的，所以我们可以直接从primes中选取每个pi进行计算即可，即
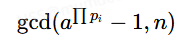
明白了我们要做什么便可以轻松写出exp了
from Crypto.Util.number import *
from gmpy2 import *
n = 210488679270475701976181947365152313699517734264122394812492020724654505220623065289117447808270300405893088216711827935540458944042230307295703758023289811232234667671779565383964487868833609515040373751117785890923111021052281871560758159098018301948230396406718130378740957192704249130990473406094468375190967933383609736557
c = 136071043914570532351840574748667342595827512223368889758030473691165475344493240895540489846178990095609930878050872170334417124306746585253763197947342333489768575699470163018093386136808345465103492262428343569799463896437045282842447134475696863670001725029430508792000363373891006638520238615750531296612676072986388618657
primes = [12817836240916621099, 9796955111076276721, 14260192631353157767, 11331104417992923271, 9514036759383573643, 12830010251405547647, 13614319430115788837, 13292666469666083977, 14743386631123002553, 14117202746451676457, 13269748845129713117, 12168813134511397211, 17228879457544885133, 11476468574713278067, 11946685680111967199, 18345865007923209077, 18303664985620995833, 9822277703479114283, 15178066358256569473, 17098068971695098757, 13618686975649185601, 11744366650084293437, 14752193726031278261, 17843527472060726393, 12389668794044063273, 10376034649713785869, 12238540175552034637, 17132154884907233137, 11734611387998570581, 17011805096670339443, 11625121908845289409, 10757305216406425577, 12462221960790002209, 16018515046461158299, 13961897238779389541, 11607654254039926417, 14764422702778633637, 15889835560738915411, 13067226817787067883, 15887483815693916443, 17641812946382237687, 17751437011380057229, 18384735831631526519, 16918144377393116651, 14150464978154164637, 13178350295174895967, 17995769690138536847, 16340079015339247603, 9398681247575712871, 13634353827184119163, 9611544156521225383, 13453176756459641471, 11303353946688525031, 18109038864474076559, 15045485267231590583, 10972199753934977179, 17574722479092926033, 18278068689901766303, 16948848653119121327, 11758909188247026433, 15665449198029497387, 10901691956952449753, 10584519935735226743, 16912467675047183959, 14327261172669596407, 15097367563320670549, 12297273221784672769, 15947284817142437047, 16781387148892629007, 15881303895526705733, 13045061948663850751, 18436681745005029761, 9233724300944854859, 13047527195762392259, 14723757760242013169, 11741005205965231159, 16408614260735211923, 13814776270447837021, 15906163142517891569, 14423435831173412623, 14612928719996598469, 10885120118770555303, 13368686720584342981, 14068267570818591737, 9868356740416745089, 12406920698251977319, 9286022127447238097, 18023608417081960717, 14923516882492986133, 13823678708930659963, 12857551861722029083, 13230742121296437271, 12729591066572154191, 15849174322092304703, 11085431171727680393, 14068906847806320077, 13851658642377888133, 12875459865393464869, 16373459542443249833, 15042636961965421789, 17804579165451279653, 13220312902184268113, 15150287797243551839, 12346428755895098357, 17020549628614536703, 16886745404527188301, 18375430790398618129, 13224710597451808487, 13359444437510262103, 11873826262101064243, 11965351035977107903, 11235458928878258717, 12997583502966109111, 13789872877795337753, 9410284081150637203, 18303250922016774599, 12282563435683491241, 14305213835649582409, 11918623460221018469, 10943597593864147127, 13038337723454095519, 15455421326799165353, 14062369863925079513, 18367836708310870171, 10613492300802961321, 14459256689604923461, 11706673732895890387, 14382736049526145057, 16655509777788355597, 14000284683606298529, 11290821241077537707, 12847958971987427681, 13809253826547615959, 14684126452952111143, 11855586041954042173, 12714825000812576869, 9459493996196289107, 9842932973342874239, 10570590695078468843, 14410685183194015117, 16898517162308994587, 15220517599820119309, 17333608782273432163, 10377521770815190027, 13122631859485901471, 11571227468583314827, 11817889822931972323, 14228001997887128497, 14456085940081475863, 10270130489745680131, 17517555821987735831, 15429383763760026979, 11108995892538667811, 17911418867778656821, 17139731172232986937, 13426013319525942679, 14562642807139379233, 14531693252415486269, 15631238547467725579, 10320658119201020257, 11575894205699157263, 15384475741355621261, 10764073960673003609, 11153595693401172317, 14790585109191523507, 10690672323080867881, 10357625576156190589, 16431064857205643717, 12130023867007235381, 13564898535871926389, 16337575470726771133, 9618083378800557767, 17232134619106506173, 16342365536104729669, 17290061582737251799, 16670033868010116101, 16394458575620757607, 13679014824205066283, 17991831450196114597, 12317978714944305947, 11632115207816943743, 15797700688884441463, 11075555837128820431, 14881723251235989661, 10010880757411909987, 18270144545531928449, 9465870609311716069, 12582412206542381803, 14662660113361450837, 16112922901618122901, 15363650898935547023, 12533640949094063143, 9470733380298789667, 10096457749634891777, 14406227249889370421, 12890530725415748549, 17792709587851953943, 10409603150957944463, 16280446889224274527, 11347835861520223063, 17984512079289457829, 13366696032094869983, 15399033257453518289, 12925451097314982419, 10778713773001593313, 17284945985665888051, 13402816621446294619, 15528594004221819047, 15809192880967976213, 13251703483278993869, 12208007531464953347, 14651975501449610809, 10384298003710994317, 15330372718569145519, 17248847366496290681, 11854891655415812011, 17751134388906831949, 10124732408491652509, 13625466395305938587, 18200378429690571427, 17452972356845950849, 14900945233126132883, 11436315090796776343, 16581798874532357771, 15111242773400135623, 17641315625748809411, 10450595023153090573, 13264757738530097911, 14485829224324514741, 13330871005549345411, 17136650784851341057, 14910153824569971467, 11210011057574992181, 11177037566749571093, 11567028438251098903, 13198253645284080859, 9785835301058295319, 11870911273186997459, 17086899150352287461, 12688798468940186353, 12829816797037704869, 13850020717472465033, 13962611682980549657, 11101821698837041481, 11707465921615682923, 12959209007506476811, 16644144509323715441, 10367003935119200813, 15453978273858403009, 15167350154202134803, 9368800879722378161, 11455175913776290139, 12851750838491254999, 17944785619839501011, 15794784996188333269, 11020878345656646503, 12895215750829198793, 16875096766698669563, 14118851151285954833, 14838789173869952831, 13751766063230858977, 17320191755949110401, 12060022464165785371, 16746856058764394767, 11340262053390390623, 18063813798829005593, 17301743539019024441, 14582876446851166253, 13522319333542791731, 17645483968819162681, 9674664037282811197, 15042492503708901197, 13403260615183814477, 15357650346222449437, 13587415537998132773, 17790598348568475959, 14937073879575692303, 16946217240852764177, 16406234190000264941, 11235987239543284367, 12490317539195443457, 10442876360637230507, 16417744334203076861, 12058149621525280003, 13299492327856068067, 11314451949936901933, 12580137629414492233, 17187303597929461189, 11472019543632605501, 10358023847683468963, 17655020163619780043, 9551405925019296407, 12313496295674301209, 10693093530328277813, 13024645634541678097, 9897976814256674623, 12205181340503455921, 11417228617170103249, 12826004690606531803, 13639934695225511677, 14590472153531475251, 17909159724817643663, 15533310761093773937, 14386571855319704297, 9316892936362161067, 17993944869296641759, 14759692394249822753, 18270460879245227951, 11182120139434421927, 16177012907245614719, 18028663420331019887, 18139576777474000879, 11213134310805448589, 17936183694734803343, 17975442509209584199, 15559262723302226837, 10180836740719706297, 18197598310364802337, 16827523931763080353, 18214986373700605081, 17585494217763004861, 11448026570948864933, 10900056287904330073, 17166645406697902543, 17570484141533117293, 12398389280142315301, 14630567076893376083, 10833999841227994577, 13299004526654333801, 10244054538116403871, 12907824831930739939, 16885467716977238273, 13880284027516293029, 10887546467303319323, 18068389832047177387, 10450635565653187523, 14726030363122148237, 16768133481946424951, 10301298929545489007, 15415018517648901401, 16206238099391413103, 16263750958615351591, 10054000098803084741, 17081860428453965453, 17951459452539869287, 11892815832324644093, 13775418173952588841, 11507176664859257743, 12436316449453831829, 11373445294062449503, 12707349516508026313, 17304366121752246923, 15088976801734008287, 14882686898562658859, 13312883733509401117, 11175338376664870423, 14995241990449050829, 13984129139378165623, 18263293614524334931, 10991047462031450617, 12865816467095731189, 12198009780829783649, 16748296422094146653, 17904593640666707729, 13792268569149446983, 13853849612423089637, 11546534301480400423, 17137023443158040753, 17905444488998063857, 11980813095592929253, 17915972690674748693, 12451065502875272893, 15286203704429102609, 15961659110687401169, 16879684083254701141, 11466389710715075681, 9862223709098321893, 13427540762341339663, 17120171216590076191, 11328200399967258851, 10181508980912484023, 15114850231267812229, 13401368952119603083, 17310327686592116461, 10812290766823212593, 13321530124771363837, 16916384745420105733, 13158876505531892249, 12781125756513915947, 11177172300491135033, 15192519949009579177, 11107570709578280603, 15790871007179692423, 14673525326882261659, 16625393027047576363, 12208173252153948521, 18151011223033756559, 14150927812081733711, 9962724536266278113, 13883267417298402779, 12239907647067385063, 17851351494511502753, 16218780803683512137, 9231060907590526171, 12561800952561489217, 13912140573946770893, 13149132600571773931, 18113853656519618927, 18288722620221293333, 16238398234781792947, 15646176443969341973, 11480617125273259589, 14298265531428974159, 18152443754281945309, 15382191810022993691, 13677302948532689779, 13044467560942628911, 14180490201042674161, 17699382878024999029, 17295445764705446263, 16639917043083590129, 18119370341032732567, 12154128334903051433, 13164685890717792107, 16936772055385035967, 15096483065553525473, 13471209141541779203, 17378837190351254407, 17426974534141344883, 17959141780827119891, 15016498199784708659, 14421160967688875941, 16740532654485547157, 14936157018002326123, 13256118391055166017, 18174072117119534467, 12090575013064577347, 13006876700311968451, 9238945670292014191, 14213473652368499983, 14243331673872027131, 15857539045385929681, 13412686116627591491, 11592325887070165747, 15608925272834295691, 14666236964631839891, 13540685243058340663, 18270373973909961613, 13828282470103450277, 17892440011286210501, 16870901545940692091, 12413729884613628023, 9266844013399220221, 9745512147631925389, 16387537652784438451, 16570045942363855537, 10568791466436873997, 10182396317953610903, 12853823905502858353, 11851841417409724277, 14115519128426356727, 12881420948009143253, 13130088098325861749, 11721786782351310083, 11236214958267547553, 16702899637167067903, 13501762358014708543, 17462031538915936859, 17276389012007923211, 10644899384346664337, 14027005255127061913, 13530526660154644807, 9844415966928882743, 11249128120835910791, 16777866679514313817, 14453045993106743699, 10996863066540575321, 12283642992171368333, 11404591589887867667, 13677761664265732687, 13110578735652791741, 16010046184639114171, 12753941270332721647, 15772567772565704131, 11831712320633880293, 13319727865432694257, 10771551848090338763, 13480980853991727469, 14248794265347244051, 10664170815864253153, 18371374206685581661, 16482126216840379091, 15311554751751063719, 11347740685464268973, 11911625562195859271, 15948182894664837227, 15833902828630883027, 10628744258695587949, 12242229966886189549, 15729900088141513717, 10331962319086103687, 17739760722083508421, 12122206963635673601, 13444533154829926777, 16919840780438603417, 14181132415499287453, 15832764916978218089, 11107329810687234827, 12537867916219452571, 15179335658283523219, 18157750076527384319, 11335208638879830449, 12778309804903027751, 12331094589527085751, 16517169709337458391, 16074354330760224817, 11121010187417970569, 17541225150843770231, 13072072021644732583, 10683918634042372291, 17818396544323153021, 18097213311786551693, 17377696366492674853, 17840289332463757343, 12300868091354913911, 12110148694323274373, 18183424490112093451, 14470426956322731539, 11537900791630973609, 12288308024287816769, 9416608386548247127, 16142185824626408983, 15319391474385481709, 17427093242388654611, 15757681760350596491, 9375203980011408289, 15281050099968592837, 13962807632993334377, 15641960043003280541, 15857385507932475607, 11328494963300401669, 18165773294104417547, 14012380629632910359, 15541214952410221769, 17008189780920470053, 14632891822044772337, 12404052309147249313, 17208994155033269833, 10635749760511488169, 12320122505182031957, 14796692998214399561, 9673910288177915309, 10047903793961297059, 11326483999844129969, 14635083490823091097, 18071773072169124043, 11341815024873111347, 9438792655485507689, 10008152749575925909, 17567654747849893279, 17061517364811209911, 17221503802511195443, 16695681584397997897, 13081948422266488091, 14625725701559358637, 17169462066133068869, 15709579351595465593, 12209792348258846639, 12122275607677157911, 13807547725741290973, 15583160659433004293, 13396260775506371641, 18217020689915921843, 15619329053256302987, 14146270775635402231, 16863952377303204673, 14548776148506068719, 14529188722082059457, 17265380804141201681, 9776286763289778197, 12466859136109077443, 9772744223809808053, 14470786313269634927, 14607320696711471221, 12455737005988354019, 16637246382861080953, 15133708215096275683, 14847081677445301901, 10332654304000904033, 11159603116014973271, 15931004335130864743, 11477160443275710217, 9535586193995849951, 11293175983668556793, 9923153586904495507, 11933006027142853931, 11128574253134634017, 11076766797263201329, 13515870030341559941, 14622814541338434853, 17463892929742334407, 12615007904997547229, 18206100766716434933, 11455838674150852697, 17479338037013854559, 13360281258747049621, 10995035322560010517, 10928474912163737647, 17726175981976035227, 11704404121506907637, 17619146892908914121, 17704564527305769329, 11812175367635269621, 13416429352943032249, 12131563217847962351, 12183503097530938127, 13981143659247294641, 10634933508011331559, 11562423714401189239, 17688490613654951281, 16861173019672178969, 11053050244878979411, 14086304443079658787, 10578453109792325141, 11682151227114266497, 17000674853229930419, 12598355342131798913, 18392805884632295521, 18431468816652818879, 10874622447515914201, 9872938674493987793, 9744625343948785841, 11255274706725187783, 13530191079590038457, 16173365083190310629, 13224430590784162699, 15969778943599937653, 14043089726984416741, 13781348214896464493, 17182476995296609963, 12896436977884956841, 15077836731319621141, 10080593144973733229, 15891293339878516513, 16043377959654964921, 12784208144845810363, 11543219604826483837, 12024729597387644591, 9777324062326177771, 11527333015686779569, 11474993589954273647, 10182859812157362677, 11376680767502967977, 13996225568082222469, 15977867067599549579, 13655821277773358029, 13297113872058771941, 9897159622397740493, 10013043069023436713, 11531819115816693283, 13710715432898401733, 15195815565078492053, 15452255999389129147, 13604937934214924243, 10904911638935266651, 17580607694180244349, 10376618524272533669, 9571446041130564469, 9825683462733434701, 14468571684404171527, 12770922639680720219, 18167455477803076531, 11465084556247891097, 12746847720200807209, 12775769479808373047, 16393448046945064087, 11652620391412172563, 11478574931730042203, 12270257063042073917, 18023307951026693759, 13974408232745028701, 17780249113700985763, 11355073357007701631, 14471311142350516427, 17473300039363624031, 9777054399339418903, 17919523597873134539, 18378677639427969179, 16777121138942295433, 10168805248401432883, 12641872323183817099, 10116977178009093853, 12176766460209633133, 10318924588276162217, 15546400482337419701, 11832021544471242827, 11215298551637042363, 13865628369013960619, 11129154280835514367, 16222330145886628943, 10818887859000996101, 12468152598968308903, 13676585842283059039, 12921766523283173867, 12089564821140624607, 10225474175631159121, 15819547992851766347, 10182914408006996497, 17167878424092859061, 11514181842204916613, 18287116051767400657, 13272824243652359389, 16648019410746154129, 11920726101309487981, 12649244363524402771, 10550622175590275827, 16618529989972308329, 17515407948374854423, 14391969260138111129, 14759186383646463271, 10919403521211062401, 12185965786265832247, 12116710629039649439, 18433362234939139601, 15965694148547533529, 12974211820712657803, 13353321620267206573, 17096739903159443939, 16696518371292656759, 14462358883896548437, 11367744283307543293, 15323226004742755391, 11746436008806326197, 10920871861266559943, 11587724236478293867, 14992265004480347113, 15708312669494860931, 17916196036842304759, 12922134467647572521, 10454128140476511371, 16430520042575406421, 17076469495651100089, 17772189207011073799, 13384875880146838373, 13935012923273198147, 15240883815131987791, 9420660305133379817, 18240375964640868173, 14678307842794601773, 15288259585116606757, 16610633684634874867, 16486217839536541813, 11661546558365415463, 12152118203599876189, 11800253185351909913, 14374602260090605153, 10449913208502792287, 10009143259393434427, 13307738699651704159, 10654277669677635361, 15407444571115834129, 16834689677973985291, 15066169839778509209, 15475733561257809121, 16380412207874211983, 17194107447716508143, 12192621570297038107, 12240237512637106837, 10441056377505748681, 17495542058396571671, 18293106931869404749, 13865897548876531381, 14113466667785343973, 17525437199295255289, 17422068598489386241, 17287527045122701379, 9455908640325923213, 17335751448105539767, 13590715372748461303, 13209806666168836589, 10261162812051097369, 17733334183472849531, 13246213547584426837, 17766000084271444483, 14150582008333438807, 16133690731517495399, 14641711413776366441, 13022351466394992461, 9226681052162486651, 12760195383928077577, 17567872876849046111, 12340487597227543063, 15563748447258497573, 15318459465935920571, 14255243227091610833, 17062529558035843303, 16176535147083208321, 15827087675880312413, 17271698018463248329, 14142147620294354209, 13914535203046847609, 11613211706825082407, 12959862789560256293, 14016596084494475893, 11293492671321492157, 18421116955007051749, 16404448288688945063, 10841598730147032461, 10668072389421742417, 11551364596378565711, 13850029337813227861, 11516141636470693969, 15920496765925322419, 14276274249919823203, 9237568470631580119, 18381932334031688533, 17659877642674983931, 11159795358572892799, 18206258071410742637, 12280903436314972243, 16038761168382463333, 12461628152852020297, 12599866901700933119, 9503462554473103217, 11481782370632833811, 15766095164814323669, 13079723298271643593, 9272657104293910643, 14060047426801456841, 13335454529166743357, 15841992693734542661, 17764709418538501487, 12160915899913859321, 14713689640122062573, 13337663648949716537, 18211158405283472779, 15158622942577374571, 11407833997760128867, 10508929620338632321, 15961989193725497063, 10501876330362297371, 12364784867218660099, 10131314553714497933, 14441100812606959489, 14721325750202554117, 13167419766289684193, 11981676591145933817, 17913851093510662607, 11835488665953985127, 16780953686692778041, 15608609099671724267, 15664551105384515119, 12802145189741653877, 16805549931391100567, 18445301756468541301, 17655249735232734959, 9689891077025566237, 14840484494159775929, 10723334034602592439, 18386904850027413517, 12096629257610342447, 13067964115598968019, 12252109817674770679, 17369822671514623363, 13509155615162956807, 16855863641920860103, 14465746296157191683, 13544016597391911559, 12971969005041850273, 12280334067500075587, 15752570905864769503, 12113525236215732611, 11664013792437359831, 10228837640437031773, 12109791131521690777, 13624111940052646099, 12777090183758952047, 12426963274674728939, 11441470375408996129, 9257227171899364921, 10191312647768104939, 11865326812561002887, 13522604753854591261, 10249599313373359463, 16159615612202096369, 9836233098999799211, 14799557554105507697, 14042255386918619699, 16477871730966758129, 16642525196644416059, 12423008258752432981, 17273875260714952171, 9470913631654644977, 11887078253521363603, 16706376900014360707, 10304459396140054031, 17693305758580051121, 17214391436952288473, 13618743595320511073, 13169249530153192079, 12035858011919909029, 12860667847247804537, 13990854606273162281, 17035861733161781977, 14770109568091276793, 17949815755824751961, 12390337922014329203, 9595001010493198999, 14690160353746242721, 16314094344794415149, 15483233288782887491, 13061397420799425431, 12076045453514601679, 15407273036788472813, 11365402888927879361, 16668884373589636511, 13828335850402659011, 13284203923815359527, 17300809842931614721, 16947803187487136093, 18225750745362866369, 9284672876803885567, 14597852340551274989, 16473939500074387811, 14300584548546758897, 10466932272724101787, 14229473210374543483, 13248150377350757731, 9598039034657163599, 12586816162498814623, 11159150798363316113, 16077108181795072301, 11161401146827356863, 17852976451365316379, 16386970647736403383, 16568117397633516523, 17674878979814499799, 14520861146176965691, 10340053725357332591, 9799386102480704957, 16097477422918098601, 13239453234793950397, 17567007567243212159, 14136045876498729691, 11732340248501116493, 10470310463829179399, 12703325772051719383, 13035241397098055021, 17395156339749341267, 9668529469335994589, 14249010465960845651, 16914660786225731381, 12310520468883701851, 16246592021694289649, 13480017886196771549, 14219082481229344661, 11647439617192501739, 12765954006551032897, 10460413869136300141, 13716846676298104453, 14503448822338349359, 11041742165867028397, 11701704236558588467, 17606212925100148273, 12342707180459270959, 15360511526093354189, 11298030030747659447, 12872763047261841389, 18232938457364630449, 14660255297113325941, 11890851251611038169, 16792857595881777097, 11852378876588707279, 15357599751372293533, 17780342512970330669, 14195457757956580333, 10658400270468681989, 15387143294376736159, 10267219662942666551, 11046696135185833781, 13885088134451378279, 10645311967978806011, 17659494527222079353, 12862971250844658743, 15093229194999614917, 16241065349609244691, 17076182031924555031, 10410526641699080551, 14619036188529238943, 16435691426252481919, 17757270819329871647, 9244265187799778663, 18317093359569022523, 11159244222937462369, 12404088147132662621, 12503445554528532469, 11834507189075821319, 16399491741674305727, 17314200642630424609, 12461073769029981829]
def pollard(N):
a = 2
n = 2
for p in primes:
a = powmod(a, p, N)
p = gcd(a-1, N)
if p != 1 and p != N:
return p
p = pollard(n)
q = n // p
m = pow(c, inverse(65537, (p-1)*(q-1)), n)
print(long_to_bytes(m))
#NSSCTF{e9991e0b-ade8-498e-86a9-bf4af9770399}这里还需要注意的是，这里我们只遍历了一次便成功分解了，则说明再生成p时没有选取到重复的素因子，如果存在重复的素因子那么我们得到的数可能不会完美的覆盖所有因子，此时则需要增加遍历次数以求覆盖掉所有因子。即上述代表中的遍历需要改成
for p in primes+primes:
或者更多。总而言之不管题目如何变化，在p-1光滑攻击中我们的目的便是覆盖所有因子即可。
[RSA3]P7（限定范围的p+1）
题目
from Crypto.Util.number import *
import random
primes = []
for i in range(1000):
primes.append(getPrime(64))
def getMyPrime(nbits: int):
while True:
n = 2
while n.bit_length() 我的解答：
完成了P6再看此题你应该能明白该如何解题了，本题属于P+1光滑攻击进阶题目，和上题一样，本题的素因子被限定在了一个给定的集合中。
在之前我们并没有详细的介绍P+1光滑攻击，因为其中引入了扩展卢卡斯序列，涉及许多的引理和推论，故将P+1光滑攻击原理作为扩展资料自行学习。在这里我们稍微理解一下P+1光滑攻击的原理
我们将p看作
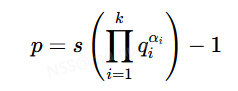
则我们有p∣Us(Pm)，而这里的Us(Pm)便涉及扩展卢卡斯序列，你会发现其实和p−1光滑攻击类似，只是p−1是利用费马小定理得到整除关系，而这里是利用扩展卢卡斯得到整除关系，我们只需要知道它也是和p+1的每个素因子有关即可。所以我们只需要替换p+1光滑攻击代码中涉及素因子部分的代码即可。
exp：
from itertools import count
from Crypto.Util.number import *
from gmpy2 import *
n = 345799778173748173773868120733939877012606206055022173086869626920649670201345540822551954372166638650313660302429331346299033954403991966160361903811355684857744142271007451931591141051285664283723609717718163872529480367508508005122335725499745970420634995317589843507796161899995004285340611933981932785753209168028330041659
c = 246232608531423461212845855125527519175008303736088113629990791124779986502745272419907699490375796645611551466345965328844415806242069890639077695943105766009969737068824735226917926112338655266209848386322013506145057902662138167248624945138207215690482597144303445656882230801297916736896978224496017358461492736283036138486
primes = [11400500846732211437, 15663612686729436797, 16146509422571674241, 10365633794353033223, 17764432204956231427, 10770086682509726701, 9363619846718624519, 9499148531156874869, 11870308229801920153, 9493684235948177053, 13439889213792762493, 13543824553169466691, 16784144744729574109, 10473345639906795589, 11686628555687269949, 13438006849184657287, 10304115634530565157, 14523860318465391989, 9647953497087513131, 14024608681547907539, 14323731752105690329, 9995822499706628503, 17263798266448817081, 17412342258647700379, 17552446328775319979, 18182174233675599269, 10926506070008989781, 11287875928373292151, 13031874421918467239, 12826862978863344077, 14427019901941927789, 10764280028896236377, 15204422422736985733, 18013581759315499403, 16196860580398627489, 12409133067619366927, 16982209362087366071, 13552847891288053379, 13321664796445708301, 13503601532891509847, 15213413154033638143, 15789125900714604107, 9661259098414185323, 10097901158936073103, 12492567105127893229, 9803017918077701719, 14959766528145744073, 16380271870181847503, 12379170631770822511, 11203599319503847699, 11697577879391178041, 14830577847345979507, 15161718518020147133, 9449134020600011261, 13590570970475252977, 14435422638900288329, 12478310842333840183, 17177994464705553637, 15072278791274696881, 15805713015714544379, 18298117834725348649, 16592677662893953627, 10360712314766543039, 12350365014973219109, 10487476039094034247, 9303193137466554371, 14317509909121736027, 10069727352579607261, 15672913494263557921, 12645137927662029131, 12577294286343986777, 17990217715164074353, 11770491954898217693, 16352325276206313631, 14742366552931089511, 17904845678435279687, 14896783599885913301, 11640348097370069257, 10229197144755015913, 16348769379755789849, 14815902973349076617, 15808546541834061079, 16180999769759067937, 11333835834203173919, 14349619526753022311, 10887563403726040387, 14696465704976418401, 16612699690876026649, 9242002307438002549, 13294711665781655819, 17316060056875475509, 16264270500305765159, 10143806453587312567, 10156382001678762061, 13424697447914832193, 9533479368240114361, 17607602236552058431, 9513935785246155433, 9348999429693542821, 10687833447600343907, 13029642955293734383, 12352583868905249059, 10578933735997257233, 14807418828818185841, 12723999174902787061, 11812631981548150111, 9469570721445804379, 10407923494920638191, 10559989029436270817, 12477140185116458017, 16418595676222668931, 18284009827664751383, 16879482079149887887, 10274017234103862649, 11495861205598434163, 13574496359130781637, 16347895315217629291, 11184342831473200427, 15117572072516544349, 11962165465299205687, 12593274795450046759, 10576401623272055507, 14871424922307314839, 9683965597938835439, 15649192958998385653, 14136512522186754793, 16189574870468706193, 10432462783789785083, 9882402816632001041, 17467673636368162091, 17812738031541243181, 16444195776814377667, 14458128171493667993, 10068762164183818769, 16785805107381133639, 14471872315245024047, 15256999419456872801, 11245045254273493879, 12432915941937754661, 16779879208564650527, 13527359679120520799, 13609212316987142881, 12048851866296673223, 9700737321821517313, 14378798305839284857, 9611124475271266561, 13852359141963480583, 11482735530462856063, 15354806409837420893, 13941285484258063727, 14725649345415301957, 14540375648816209781, 15268062151789994279, 10710080489577786817, 15918894791610440369, 13679067272608182587, 12130148919788574667, 14787273033558048851, 16823039346693535453, 9786912554506032653, 12271391359749298573, 10338204530215094879, 17031700055987188007, 13892013056459801951, 16466462551586874361, 15509765092722859157, 17798707991935554641, 16724399949431954029, 13950635476447170409, 11844033699047785357, 14747361128582919509, 14667470964266641091, 12896901039793154849, 15536822808734549341, 12385771205898361763, 12265293491880919333, 9519013453753799311, 10399041997001597659, 16593843155091891947, 12731251001624534627, 15446540709384042589, 9977945635496326949, 16022582598611495171, 11602170089144567501, 14556919126878807737, 13325795480553101047, 12141291839761394549, 11056079849427396533, 9319147679594339663, 14076618445093460089, 13279302183770932003, 15969822774426507863, 15634577535247166641, 18134435225679362561, 13580840906683365127, 16932745671449749507, 13861858882551833521, 17059312054729866107, 16159631686544375273, 13252534105662820201, 12853863943245116791, 15045628398991754593, 16867564338626531897, 15053346821310993907, 15424243202794355417, 12169322810803770263, 17562408967112815189, 14696130091108860479, 16353873170264652727, 18137634119608386217, 13853870828606368123, 12138232181730621971, 17695562390286922187, 11482149834977336341, 11263040235574897391, 17516386258426598267, 11729599409349513977, 16344325675031393033, 9487998624331072613, 15548753174223167923, 16246946533494280441, 15168068556360396767, 10988949668785042289, 16578604258551502499, 14921063374278681199, 17959209918307585553, 13403422202954306417, 11008060381939288823, 11996269609545097451, 14304683665387573597, 15127244416475972951, 14638939931196152921, 13736677778855498231, 17587444419861411713, 9712574859471189721, 11754669647509862399, 13808458314511168667, 14076346964677125061, 14296229481633724123, 10546969810734077257, 13806516637777666997, 11595089909651297627, 15383693545718169527, 11899557291952040539, 11892231220794860827, 18090056242513773299, 16535424213022634657, 13429292459383177121, 10938466758053648591, 13247568010483593953, 14353179575611187827, 17247884385077903059, 15492418843846011163, 13991533281715009171, 10648224887308767149, 13434464420280213799, 18308741750842750223, 16958163859863247583, 17331583790580132911, 16594103882668531169, 15654309992707438321, 12143487125851071209, 13917462550122657373, 14300594316387726833, 11038403267265055433, 11668215065573927149, 16522831969819412009, 15574426807839180587, 9521082951973994111, 11184051603632666453, 17420808937992910057, 12911596655426162347, 14013571659883359853, 9255799220881949201, 10863148313680771943, 15125487406888857311, 10787391261037964801, 11181016652346500041, 12375758200228628333, 11096658214489080743, 14127930959020578487, 11097748121705255807, 9576959296273172197, 10329268625923900369, 12989481583199396267, 11221816342693962053, 11682824873199396701, 9726906501816888893, 14262866113962178411, 9585657969091757713, 11560990155825686603, 15431631822377633897, 9693653500895246153, 18052885089925870411, 12230353179628084643, 11140231161527021251, 11692996241065359677, 17325167313903580247, 13625405742824607707, 9700735722329114107, 17772484003012329121, 14710477009444476553, 11461459386714361369, 9710381370263165737, 14182228639237393261, 15344135038819224257, 13747712780102897047, 18043450369219899473, 10108489789901066423, 18323581078801222739, 11709502836760188211, 14510120896876508611, 10099898624211195287, 17361096065683222901, 15111530145788039651, 16726669802715322249, 15303048960860878433, 12918404780084443421, 10395837535719074069, 14881964221907324279, 14275096296552385127, 16767210669789926149, 16926825798156482309, 12118163891694788129, 9527147805191785667, 15014015486557066933, 16813575270918372811, 9593601949025443639, 13896995817956105537, 13741986219854107753, 11144899659720022073, 18238128043240764319, 12779733553193717153, 12771981722317523603, 17736020578173685219, 9340904375029821481, 17592111347118520843, 13580882292330428401, 15018369925699389031, 17809424700118883129, 11613026101864549847, 17286309683170750757, 15302812145728958509, 15391566078527070121, 9974325230682765697, 11551570786966900967, 11351003337990798203, 11120412046865048101, 9696688946725965169, 15093528920040797497, 18065996667394084837, 13292251568744035337, 11101213198305556951, 17531999985277474517, 15966406176658019221, 10691542704039725009, 14297474600370306949, 13621179047848909531, 12859649057819536667, 15917449527351930353, 9605987875906658413, 14998884139877113397, 9303906426219476507, 9871680222005313013, 18053630596736423699, 18214702298732770603, 15217549802969404841, 17230806139959259801, 9756053496476979851, 13493983446716093807, 15872062367640353111, 10830618212258286257, 13343744885931835489, 15379338915986533049, 16664848187297516537, 15913611403024361401, 16957002785994856157, 16999268043777708043, 15924602242524984389, 11470115363514206713, 17780900375430786271, 17219602318975762861, 15562078753739245099, 14429908225005981979, 16785776318383823977, 9345347283569848891, 9826037803806928201, 14757441108506302691, 16843056852903557147, 12089182103754698633, 13071844903007200927, 13309532659259919281, 12185211383730425707, 17671246663671372547, 15827919662605196687, 13921392459246207437, 14214028972975886279, 10666188887784923113, 15026095328389680481, 14070638370052382317, 11515225275289974647, 12733768797899627857, 15232090050353579959, 9605577513419872349, 11774332933083185117, 13015628182391854561, 12452018187207611071, 10613040759167447969, 16395318189590579111, 9650312608310268509, 16507662966772496023, 9745403684063805119, 15429094458205621159, 13907939611582114601, 14350669162433050921, 12444630576676286983, 12382608458977480781, 13701560178384085519, 14561536331132891843, 17870839403342285053, 17726305914129360941, 18120422155613702203, 11458486193501014487, 15652084560104054171, 16016407186905293131, 12896826502049676533, 13137573987547216019, 11993148289033574989, 12553485329707332011, 9407004537495583253, 16551197209131499807, 12188240888329030727, 13138059982433827393, 9447792088431441973, 13898552597307352607, 13086125839706222777, 11253297961067347699, 12473509293771699973, 12025629766486534463, 9246425606391056513, 10978614475595947261, 15328005120420669143, 15005188618611818149, 14681521764654667837, 18222824871931463471, 13727103721842925123, 11056314452399736701, 14190514709890056683, 16071925700301971681, 14114206274338698617, 11354892818254049171, 15558048570303377969, 9548803747853081857, 17588526935062502339, 10932175915126889777, 14848760934877079473, 16531929394433046437, 11059255418387621143, 15419998777650574619, 18133329784854851773, 9376742948363866007, 10267333769360440369, 10455930081787849081, 11749403554374261673, 12289480767522531263, 9355881077811916589, 16377906719131687771, 12636537540548202157, 15473661167864858659, 12939130785963130559, 10331428178834892869, 18403302396935375239, 12457052115957020359, 16728650241949106683, 15673023018343436269, 14566008317650142029, 10428852531127223779, 12989287388538384809, 10023218474904646751, 10216986934332559607, 11200524499033897849, 17374818422359302449, 11795887296034843123, 16260134950019402467, 15545049906898796849, 13905976122896835137, 18192952532376915133, 15245754103999312679, 14336092681672892797, 16711051263995536291, 10268633000776041389, 16298601116274769289, 12526591346109970043, 11057407454514514777, 17316528792225617197, 18057651102128098207, 16192203874370581303, 10293184135563422201, 9723556212482431513, 18054422790317350181, 17756547295472446751, 11552860515549111289, 13432033735566726419, 12179716429669289003, 14947157147090126191, 16335353494729459423, 15184076846117432761, 14777743253109667273, 13625241580579004263, 10998645430939015469, 13534322946405781903, 11327079738013968217, 17487263803711590509, 13189162879894145159, 13784538619743485863, 17064328079090046263, 9685004881707057761, 16079690295682955971, 13294545125605834661, 10648658009947462261, 18415164681671251511, 10641837226629144139, 15777331516260137267, 11795948058583766659, 15535152465440663291, 17216667014436648943, 9653047732094860031, 11131348011090342127, 16886193462362116063, 15612491590607382593, 10835879650784394071, 13279435351244340899, 16168298479453780489, 16083456466830550283, 11380553957000451991, 15128521211355953573, 10826365584345090827, 11931387899927297363, 16091037230044064021, 16855367086926162211, 11170558557176459503, 9886757544769944653, 11450033604282275011, 11929757603936817763, 17420827560223252171, 10870631368466407877, 13834307981276745037, 10230994628690765197, 14461440966371289941, 14513569082524554649, 15609519179461790747, 12452462947852628413, 11697783772313307211, 10077360532646539567, 15668479810095426521, 14100390060574107281, 16039433251746746399, 11594255700072389497, 11335433960775286819, 17135850578547822607, 17715472259313599723, 9872560666658691277, 13426738927194861001, 9559405911145488401, 9560643982657333219, 11125735716442543571, 14348305982295065537, 17334821829789014189, 12062975303975394341, 17675818288232614691, 12456667873905594329, 11330845594517002613, 16817880606791218753, 9524369250258419267, 14531988631115581537, 9721408134124289899, 16662586589444720647, 11325110890618816411, 10051647873079811617, 14536021166978233733, 12224386731517653097, 17640459671249984461, 16543114235733129481, 12834813684653021713, 13050693286566514921, 16072783334843947421, 16824355675011368569, 9665639317029622411, 15966237013384955239, 14787243991682533471, 14167620861073328777, 16552060845197660033, 14426640096605498107, 11250797705828570411, 12830939822208389821, 15292466542716343963, 9917855814946199189, 10442126201651355433, 12042544592582006819, 13742543708854176911, 12519797425611830609, 12305049189690830747, 13048815356624492777, 17928797470734483373, 9345743880343852493, 17394449011144997203, 14027454725211775843, 15325951436202259889, 14089580406354666877, 14985891805973997229, 15815861666300600207, 13010491061439139729, 17474295865525658119, 10856321689902733963, 15719997391332198931, 11798694284977436299, 11131916950543733651, 14728548632909038181, 15869387205433439081, 10635187834937273627, 14844816583829681107, 10707745831589845607, 16061495585562724741, 13860352348388954479, 13839169685364641087, 10246021025120950757, 17909700734377694141, 11494364438621610881, 16304619707693032889, 13720492814063169997, 12550911015312791057, 18076672670188884121, 10384906691343925679, 16486782778290044783, 12644175422114478653, 14955139942049789357, 16026396184113858703, 10524600442649861959, 11001050498566874027, 9979271448704886613, 13030132484834300659, 15230981971792316689, 15374177218176283253, 14195651389624938953, 10455638721836517437, 15149204128873840301, 12500463654517686493, 13475842347378678719, 12974353406746765043, 18081547614319419917, 13613920396906170893, 18201655698843944801, 9908359973067294049, 12259133230997142013, 13435886340259808407, 17657174880994459697, 13940231287221357463, 16592426911225206653, 13749631155096260533, 13579552974478309459, 9836712372149870281, 17218778541380165767, 10464000360382809991, 16777832929341727297, 15972158110380610507, 15350561171111592953, 9938731346590575421, 17912262447858075839, 16137701207062825711, 15626368583424185491, 10499152290055372079, 9382357912889286797, 14085852927258985099, 18393486728568017383, 10652476457160311261, 10527374223100330091, 17264120882113825487, 10885171609551829193, 16296935971967210533, 17039844827041640479, 16608078020248577041, 9554142078243712343, 12151602751600242503, 18333639542063204713, 12302756704018880831, 11612577899799494441, 13180093129135727227, 15533144054803240961, 17221156035305318801, 11685681018084321637, 13339338584418108371, 16764312293446072699, 9609715328254190099, 12015164966002919969, 17640110779197465353, 16460183428670473871, 13819867905621355469, 11784001662482246243, 10882776393768075541, 12284523803945957717, 11453117866254103187, 10672997245980076939, 9837424460088812963, 9456987736164381311, 16476068953424599633, 10714497365388454843, 11566321267685570027, 12258500729803839241, 13565509018611395453, 9837508107087665041, 10883021385911688053, 13236085185545218621, 12903549664178814119, 9277313810593502131, 15325552562767494059, 15737855390072711723, 12902145372862611967, 16617731535068412919, 16192918114406845313, 13329973263696065593, 15118904191983404627, 9421694107495493981, 14757389355512560711, 11755446033555771161, 11174113824848691089, 9931655160887834537, 13952179663695071047, 14628647895265937389, 13965103496050821571, 12334188065189399611, 15026324919476931311, 13737352569679199609, 17292288948395152463, 9747700181588759561, 13039199615231288567, 15048237407823618463, 11672237438639568239, 10302962861342428331, 12445128229021135679, 14463159840208815601, 13915082057723091419, 17505306824019415949, 12290525908208358407, 18446406381021364073, 11883272894488841837, 13151315617170041119, 9986202098577177283, 11376286496724079633, 17072429507581144597, 11601908054173197833, 12769100713651410277, 11578625980850143169, 15395413375327895911, 13942489248348359849, 16149741548915905429, 13745316489572365673, 9342391586010481007, 13460580618329867983, 15049385889346014431, 13567657641395719637, 9610206585474156637, 18361259735535581597, 16345044279841976141, 10386175636785013831, 10339319734960152623, 17118190675556320687, 10005962451642889201, 14773420480883046503, 11178361855707216889, 17257848339780864089, 17226047946161423507, 16460175468823544401, 15971530319487090739, 14842029296369602163, 15224121827462937979, 9275527308938870173, 17041103378156856689, 13801145680164940003, 10285279638830544209, 13671894824963549641, 16032778609020511861, 9851225257145555347, 9375022299108554971, 14826523109553586027, 17124217400159528447, 10713407734688191177, 12691625640419643317, 15981484460492567717, 9786795565103681819, 12556711015687803709, 11148645018758728049, 13265323147276427401, 13967986650812662373, 17848752154332550457, 9981768723976662007, 14998022968536079123, 12174071201870356879, 11520148746512983013, 12705359135922834167, 16031947192061029513, 12785255613650486969, 17794207197348321059, 16590130444003836701, 13051020119617841899, 18329540394916509391, 17016883109643488021, 12739110953512934191, 17294655201856917067, 11058626020237830707, 9462906708710154961, 14623360900124309369, 11254845081678452897, 14264002816761276253, 13102001758655038643, 12108869081174715287, 17010826574740201271, 14037017483914942313, 13985137272262919353, 9633084395035385983, 17241078172401921151, 16214027901908512283, 16093436048900321317, 14391957124445034917, 12359483645035302161, 10438778853819832753, 10567110128884566343, 10292970247351191901, 16822209722672159149, 13496565983843091859, 11841500670757876693, 11147505811854389987, 14065276166663767481, 15145625093242694749, 14413829172406893583, 16503017312704021103, 11981873548328345323, 11909212497608981689, 10679989447819664377, 12423178332387828413, 14358836553490758151, 10237468755767323591, 9735039457556049641, 9478522344708755909, 17979691433619404903, 17873209010991434147, 9550618472816953163, 13347619619192035741, 14530641313417809089, 13994703746676143779, 9559733892621448897, 10382805841803379711, 11843672223274874071, 16815833185277434981, 12381223102021820597, 15258305081721389239, 15136515056658706363, 18126727588656279323, 10697455619860328677, 9352124924523425581, 17295005245325754503, 14177782902523557389, 16249970306053067029, 17425431521899489447, 9366637040493563183, 14547545849198299667, 16839246487745686313, 10125673509176340733, 16315331794598305291, 18287303257171869707, 14082462954685803851, 15710924897106988277, 9846789987736297901, 12850810892277384811, 9503762183847119159, 12035363414252005649, 12548445170155094227, 9987078241115445023, 11170994807091443339, 11647765960869059809, 10834387862974757999, 9838865006047239157, 12019744644188767517, 14761339868466177863, 10956244424237933677, 10577167950528154373, 18401121224902652879, 17235712984492843111, 18429975080980393459, 16975328717308835227, 16212745888436855227, 15748060839664004279, 10802710007407091591, 18005654473259312323, 17728864727324757541, 9476823236759120071, 15715719744380211089, 11317957584932242129, 14263043570269209481, 11885161440852975761, 12759119296561192847, 16837757861450897923, 11387051211693970223, 12990690679215047009, 15370437666068796491, 9661293882813929899, 16671594122227576891, 12760716047967713053, 15836846371629855617, 15372573498823277741, 13037801868101928847, 9227832155694778921, 12305150816980735891, 15210658418843137207, 16788466837458690557, 9762486133521181153, 13371940588733082221, 10152546759088309507, 10848887643327358249, 17205964303284825847, 12583799778495365419, 9672644823779940799, 16479122731650726673, 11829095825108299229, 16856643509258471717, 17729801070393904861, 12446898694377908053, 15647792035238488259, 15262980088834134317, 14842714080641230361, 11892658365659114837, 15543608752847397577, 18134628238866132559, 17281754915383504451, 14880763471671790447, 18365273826942699029, 10593576240664735397, 13738012363336486327, 10585528712941671061, 15236197766771889647, 12962016451203849439, 10115648256105130097, 18284391657729233963, 10065785450550899873, 14857920561664507949, 16030693837709372611, 13900562821391763329, 12228162083162590063, 11182799187528291871, 10214055412817190283, 15460696099737060427, 12382626153236584387, 15465251424009421147, 16965031217756582281, 14126243176626361657, 18080871035396853247, 12890579554268090071, 12213352895923847441, 11657388029153192717, 10594146346641284267, 10061199141387371213, 11654321642876196877, 9824908207222632341, 9667965027898668031, 15337259287380080431, 11343809882060699179, 14165912342048965513, 11858958254391153371, 14644267317090978181, 15243216027706161023, 12709086352105620721, 12699306874452850307, 9623280468372066131, 12147185253639241291, 16601705326867205539, 10344891266561865029, 9295392664898294891, 11337442576012179707, 12437074606171059809, 16257047214863286941, 15963251223708366749, 9796716955285549447, 15639176349316312987, 9957650134111703227, 13427963685313160311, 14969656757466500147, 15214704302669139497, 16883998205231447767, 9582306718565802677, 18213300288961503953, 10133964032925729329, 13921564103985671879, 18189260807943763691, 15990390439904555291, 13338552747826262603, 10004697650349190067, 14464165999372352189, 9264423096518569807, 16223738667762317267, 12581099710736152931, 16783603748986153523]
def mlucas(v, a, n):
""" Helper function for williams_pp1(). Multiplies along a Lucas sequence modulo n. """
v1, v2 = v, (v ** 2 - 2) % n
for bit in bin(a)[3:]: v1, v2 = ((v1 ** 2 - 2) % n, (v1 * v2 - v) % n) if bit == "0" else (
(v1 * v2 - v) % n, (v2 ** 2 - 2) % n)
return v1
def ilog(x, b): # greatest integer l such that b**l = b:
x /= b
l += 1
return l
def williams(n):
for v in count(1):
for p in primes:
e = ilog(isqrt(n), p)
if e == 0:
break
for _ in range(e):
v = mlucas(v, p, n)
g = gcd(v - 2, n)
if 1 [RSA3]P8（共模攻击进阶）
题目
from Crypto.Util.number import *
p = getPrime(700)
q = getPrime(700)
n = p*q
e1 = 3*getPrime(16)
e2 = 3*getPrime(16)
flag = b'NSSCTF{******}'
c1 = pow(bytes_to_long(flag), e1, n)
c2 = pow(bytes_to_long(flag), e2, n)
print(f'n = {n}')
print(f'e1 = {e1}')
print(f'e2 = {e2}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
'''
n = 17258060066893213074755453373218306582162826137762311133274776357570753221703880922246758313805944651653670388312409120584883194670296622866672717977722186711567375015117429341498055534372807872455441738225834253639068425012163751145785603722177526607324435641434593514768226599401862097301050185867830575469303960864978407638846270971263106481892520999227504152184478241946941685206875783621912245612463394268401327595737
e1 = 159897
e2 = 192273
c1 = 4595717262826082372249114022806610849627020753616385658397281529962210282956290111008418210778140550163959636029533312923781864970753502714169965973507425352493857361069899079130259227540344021591878554631845093918021212295485108865566378903346061480239406752062655328184620669486561050933167981474236084817766063901438798437061213111422401822238367462990085699301757131570089105471117732589635966783817714928153442984943
c2 = 6930904879823636264189052321687613173304614320999504775391013591790100775422558030373964338538540537224825701022993433544854997668153296576460906623734663341340853498020227553815076511099480950225109778895193096753014911735040516576988675988526232648772153671745762684830032445024652478629766700037603250123679920127263565322009118867116958069937438887437206234970465675161823446396025302570020058273271974621280101050077
'''我的解答：
很显然这是一道共模攻击进阶题目，不过还是和其他例题一样直接套用模板得到答案，原因还是这里的e1和e2并不互素，是的本题又和扩展欧几里得有关。
这也是为什么我们大费周章的在前面介绍扩展欧几里得，在本系列课程中，我们会选择性的着重讲解一些非常非常重要的思想和定理，所以如果某个思想或定理我们千百遍不厌其烦的进行提及那么则说明它是你更进一步的必经之路。如果你不能还没有掌握那些则暂时不要好高骛远，应该静下心来潜心学习。而对于其他不是太过重要的内容，例如P+1光滑攻击涉及的扩展卢卡斯，我们不会做过多讲解和介绍，你大可只需知道有这个东西即可，当然若是你自己的学习、研究路线涉及那些内容，你也可以通过我们给出的资料和方向进行研究学习。
回到本题，实际本题和以前很多题一样，我们将m3e看成(m3)e即可，这样我们便得到了两个互素的加密指数，再做共模攻击便可以解得m3，再进行开方即可。
from Crypto.Util.number import *
from gmpy2 import *
n = 17258060066893213074755453373218306582162826137762311133274776357570753221703880922246758313805944651653670388312409120584883194670296622866672717977722186711567375015117429341498055534372807872455441738225834253639068425012163751145785603722177526607324435641434593514768226599401862097301050185867830575469303960864978407638846270971263106481892520999227504152184478241946941685206875783621912245612463394268401327595737
e1 = 159897
e2 = 192273
c1 = 4595717262826082372249114022806610849627020753616385658397281529962210282956290111008418210778140550163959636029533312923781864970753502714169965973507425352493857361069899079130259227540344021591878554631845093918021212295485108865566378903346061480239406752062655328184620669486561050933167981474236084817766063901438798437061213111422401822238367462990085699301757131570089105471117732589635966783817714928153442984943
c2 = 6930904879823636264189052321687613173304614320999504775391013591790100775422558030373964338538540537224825701022993433544854997668153296576460906623734663341340853498020227553815076511099480950225109778895193096753014911735040516576988675988526232648772153671745762684830032445024652478629766700037603250123679920127263565322009118867116958069937438887437206234970465675161823446396025302570020058273271974621280101050077
_, s1, s2 = gcdext(e1, e2)
m = powmod(c1, s1, n) * powmod(c2, s2, n) % n
print(long_to_bytes(iroot(m, 3)[0]))
#NSSCTF{9f6c0e27-0c56-4612-974f-b781c06663fa}[RSA3]P9（AMM算法）
题目
from Crypto.Util.number import *
import os
from gmpy2 import *
def getMyPrime(nbits):
while True:
n = 2*1009*getPrime(nbits//2)*getPrime(nbits//2)
if is_prime(n+1):
return n+1
p = getMyPrime(700)
q = getMyPrime(700)
n = p*q
e = 1009
flag = b'NSSCTF{******}' + os.urandom(100)
m = bytes_to_long(flag)
assert m.bit_length() 我的解答：
熟悉的套路，不一样的味道，本题我们发现e和phi又不互素，之前我们遇到此类题型时可以分解成因子求解然后再CRT，但是这里我们发现e和每个因子的欧拉值即p−1和q−1也不互素，如之奈何？
这里我们便要了解不互素的情况如何开方，即AMM算法
AMM全称为Adleman-Mander-Miller Method，原算法只涉及了开平方根的方法，后续在论文https://arxiv.org/pdf/1111.4877.pdf
补充了开n次方的方法
我们先来考虑平方根，实际上AMM开平方根的思路和Tonelli-Shanks算法一样，这个算法在本系列LCG课程中有介绍，它也是一种开平方根的算法。
对于x2≡r(modp),则说明r是p的一个二次剩余，令p−1=2sq，我们有
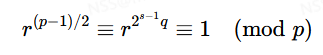
关于二次剩余和上式的证明见Rabin攻击。
如果这里的s=1的话，则我们直接有
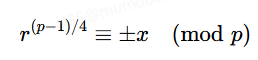
是不是在那见过，实际上这就是Rabin里面的开方过程，在Rabin中有p≡3(mod4)，即p=3+4k也就是p=2(1+2k)，那么也就是p−1=2q的情况。对于其他情况两边开根得到
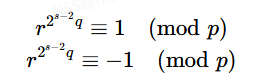
因为开根存在俩个结果，所以我们再乘上一个非二次剩余项即迭代过程中的n(2**(s−1))*qk，这有什么用呢，我们通过控制这项中的k，如果k=0，则乘上的就是n0=1，如果k=1则n(2**(s−1))*q≡−1，便可以得到
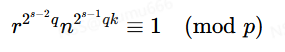
这样便消除了−1根的影响，我们不断迭代这个过程，直到
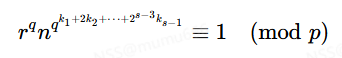
此时乘上r再开平方得到
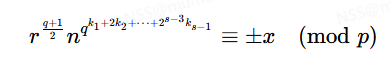
这样我们便得到了x的解，当然−x即p−x也是一个解。
这里你可能又会有一个疑惑，在迭代过程中不是有
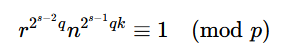
直接这里两边乘r开根不就行了吗？我们可以试试
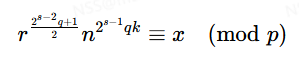
之前我们说了2sq+1=p，现在请考虑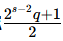
是多少，很显然我们无法判断这个数是否存在，例如23⋅5+1=41，但(23−2⋅5+1)/2=11/2，而我们所有的运算都是在整数域上的，是不存在小数这个概念的，所以此时对应的原式实际上是不存在的，因为根本没有这个数，式子只是为了显示我们推演过程中的中间步骤，所以我们不知道迭代过程中哪一步能够使得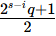
存在，但只要他们满足式子同余1时我们才可以代入乘上r开根计算。
这里还存在一个误区，11/2不存在那计算11⋅2−1不就行了，显然这是被之前同余的概念所影响，在进行同余的性质运算时要注意同余的位置，我们现在的计算位置在指数上，若是学习过之前RSA课程的同学应该还记得我们之前讲过指数上和底数同余方程如何等价
即a1r≡a2r(mod n)等价r1≡r2(mod (n))，所以这里你要进行同余替换时2−1是模(p)=p−1下的逆元，而显然gcd(2,p−1)=2，所以逆元是不存在的。
对于任意次方，即xe≡r(mod p)，此时分为两组情况
1.gcd(e,p−1)=1
显然我们每天的RSA都属于这种情况，直接通过求逆元当作RSA解密即可。
2.e∣(p−1)
令p−1=esq，同时因为e也是p的e-次剩余，所以同理有
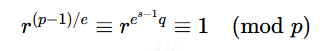
（高次剩余的性质和二次剩余类似，证明过程也相同，同学可参照二次剩余自行推导）
同样的我们找到一个数满足q∣(e−1)，此时我们有
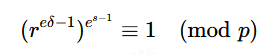
同样的，如果这里s=1，我们也直接有
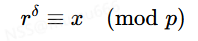
否则我们再取一个e-次非剩余，即满足(p−1)/e≡−1(mod p)。
令集合K=K0,K1,…,Ke−1为
此时我们直到Ki=Kj(i=j)即互不相等，且
同时我们还有
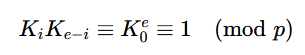
其实上述内容如果了解群论中循环群的概念的话非常好理解，因为集合K其实就是一个阶为e的循环群⟨(q)e**(s−1)⟩，当然不了解群论也没关系。后续的内容就类似开平方了，有
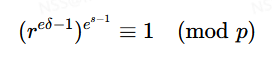
两边开e次根得到集合K中的一个数设为Ke−j
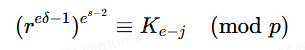这里其实就是本方法的重点，也是我们之前为何要构造该集合，在二次中我们开根得到的是1，而这里则不同我们直到e次方程便有e个根，那么对于这里的
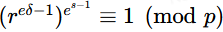
来说，他们的e个根其实就是刚才我们构造的集合{Ki}，他们都满足Kie≡1，所以开根后的结果便在这个集合之中
后续的内容其实就很简单了，其实就是根据它的值不断地乘上Kj使得
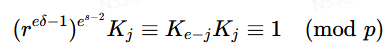
即
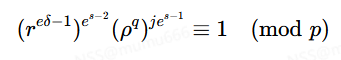
这样我们就完成了一次降幂，最后我们不断开根相乘，直到我们得到
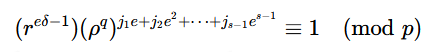
此时我们乘上r再提出e次方开根即
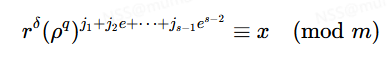
此时我们便得到了其中的一个根。
同样我们还是这里解释一下可能出现的疑惑。
1.为什么在二次中开根直接就是1？
实际上这是特殊情况，二次中你依然可以构造
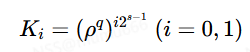
你会发现结果就是
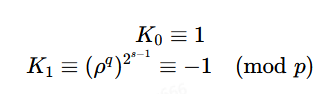
2.为什么开根的结果一定在集合K中？
一种朴素的思想是因为集合K就是所有开根的集合，所以它在里面。
这里实际上用群论的性质更加严谨，设结果为
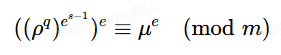
所以
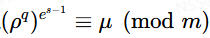
简而言之这两个生成元是可以互相生成的，所以他们构造的循环群相等。即K=⟨⟩。
回到题目，我们用了大量的篇幅最终得到了结论就是我们可以对模p意义下进行开任意次根了，那么我们可以把题目转换成
再通过AMM解出
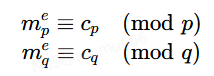
注意之前我们说了，这只是其中的一个根，一共有e组解，所以我们还需要构造其他的解，其实也就是构造这个解的集合，对于mp来说，我们只需要让其不断乘上集合{ri}即可，其中满足rie≡1(mod p)，即可得到所有解（因为(mpri)e≡cp(mod p)，所以mpri也是一个解）。
最后注意，如果我们的flag足够小的话，则直接可以在mp或mq的集合中找到flag，但是本题明显我们的flag是有填充的，所以我们需要再将集合中的所有解，两两做一次CRT，而其中就有一组组合可以得到正确的flag。
exp:
from Crypto.Util.number import *
from gmpy2 import *
import random
import math
n = 38041020633815871156456469733983765765506895617311762629687651104582466286930269704125415948922860928755218376007606985275046819516740493733602776653724917044661666016759231716059415706703608364873041098478331738686843910748962386378250780017056206432910543374411668835255040201640020726710967482627384460424737495938659004753604600674521079949545966815918391090355556787926276553281009472950401599151788863393804355849499551329
c = 2252456587771662978440183865248648532442503596913181525329434089345680311102588580009450289493044848004270703980243056178363045412903946651952904162045861994915982599488021388197891419171012611795147125799759947942753772847866647801312816514803861011346523945623870123406891646751226481676463538137263366023714001998348605629756519894600802504515051642140147685496526829541501501664072723281466792594858474882239889529245732945
p = 5220649501756432310453173296020153841505609640978826669340282938895377093244978215488158231209243571089268416199675077647719021740691293187913372884975853901554910056350739745148711689601574920977808625399309470283
q = 7286645200183879820325990521698389973072307061827784645416472106180161656047009812712987400850001340478084529480635891468153462119149259083604029658605921695587836792877281924620444742434168448594010024363257554563
e = 1009
def onemod(e, q):
p = random.randint(1, q-1)
while(powmod(p, (q-1)//e, q) == 1): # (r,s)=1
p = random.randint(1, q)
return p
def AMM_rth(o, r, q): # r|(q-1
assert((q-1) % r == 0)
p = onemod(r, q)
t = 0
s = q-1
while(s % r == 0):
s = s//r
t += 1
k = 1
while((s*k+1) % r != 0):
k += 1
alp = (s*k+1)//r
a = powmod(p, r**(t-1)*s, q)
b = powmod(o, r*a-1, q)
c = powmod(p, s, q)
h = 1
for i in range(1, t-1):
d = powmod(int(b), r**(t-1-i), q)
if d == 1:
j = 0
else:
j = (-math.log(d, a)) % r
b = (b*(c**(r*j))) % q
h = (h*c**j) % q
c = (c*r) % q
result = (powmod(o, alp, q)*h)
return result
def ALL_Solution(m, q, rt, cq, e):
mp = []
for pr in rt:
r = (pr*m) % q
# assert(pow(r, e, q) == cq)
mp.append(r)
return mp
def calc(mp, mq, e, p, q):
i = 1
j = 1
t1 = invert(q, p)
t2 = invert(p, q)
for mp1 in mp:
for mq1 in mq:
j += 1
if j % 100000 == 0:
print(j)
ans = (mp1*t1*q+mq1*t2*p) % (p*q)
if check(ans):
return
return
def check(m):
try:
a = long_to_bytes(m)
if b'NSSCTF' in a:
print(a)
return True
else:
return False
except:
return False
def服务器托管 ALL_ROOT2(r, q): # use function set() and .add() ensure that the generated elements are not repeated
li = set()
while(len(li) 其实最终就算暂时不能理解AMM算法的原理也没关系，我们只要了解AMM的核心功能当作黑盒调用也是可以的，不过一定要把exp最后的执行流程搞懂，不然题目稍微改变便写不出exp了。
[RSA3]P10（AMM算法进阶）
题目
from Crypto.Util.number import *
import os
from gmpy2 import *
def getMyPrime1(nbits):
while True:
n = 2*1009*7*getPrime(nbits//2)*getPrime(nbits//2)
if is_prime(n+1):
return n+1
def getMyPrime2(nbits):
while True:
n = 2*1009*getPrime(nbits//2)*getPrime(nbits//2)
if is_prime(n+1):
return n+1
p = getMyPrime1(700)
q = getMyPrime2(700)
n = p*q
e = 1009*7
flag = b'NSSCTF{******}' + os.urandom(100)
m = bytes_to_long(flag)
assert m.bit_length() q.bit_length()
assert m.bit_length() > p.bit_length()
c = pow(m, e, n)
print(f'n = {n}')
print(f'c = {c}')
print(f'p = {p}')
print(f'q = {q}')
'''
n = 98950849420612859614279452190318782153029931966597217314273823358984928689736597943774367572478091193816498014404387458350141854427041188032441028722132300155987022405432547244436252627801235200799719531840755071562539171489733346246951714886747673950900290905148318965065773167290984966067642777528454814019184856012497536781760044965489668142694134954466581148235162435617572891367282110999553789319439912296241889469226304877
c = 22561646796929363815984273658718096881828574147472740106912668949512978818367595303883956088667384207835022579136977262135029404640598574466248596921339941958216824486529066880854722372158998556902335323841170236300423638675072077074005797219260622119718558697081430219981494670569821476853158740209737420919480047033900157150865588466910802691118334480300332681763467974691587834295938999022060676767513865584039532912503921584
p = 33918986475509072603988274492338254523919682179700323084167169617716245684540055969194500298976880885466534900490327133434356902533524212744941101469238500990334546197257933040365697281122571898438913033813040027859
q = 2917270228344219924472221188897798789902618263281810355113281879157575741497356945522168552316357276417700368971563177551494320723579146612010452353273237547587402941227901795977981691403950826343318848831462080703
'''我的解答：
本题可以作为对AMM算法的作业题，如果还不能独立完成本题则说明对AMM的掌握仍有欠缺。
这里我们会发现e和q竟然是不互素，但又不完全满足e∣(q−1)，此时我们不能直接套用上题代码，而是要分开处理，对于p来说，我们可以按照上题流程
- AMM算法获得一个根
- 获得所有的ri
- 相乘得到所有的根mp
但对于q来说，我们需要将m7看成一个整体，此时1009∣(q−1)，所以我们可以按照上面思路求得所有的mq7，然后又有7⊥q，所以可以按照RSA得方式直接解得mq，当然这个顺序不是必须得，你也可以先解e=7的RSA解密步骤，再解e=1009的AMM求根步骤，都没有关系。
最后我们再将mp和mq的集合俩俩做CRT，得到最终的m
exp:
from Crypto.Util.number import *
from gmpy2 import *
import random
import math
n = 98950849420612859614279452190318782153029931966597217314273823358984928689736597943774367572478091193816498014404387458350141854427041188032441028722132300155987022405432547244436252627801235200799719531840755071562539171489733346246951714886747673950900290905148318965065773167290984966067642777528454814019184856012497536781760044965489668142694134954466581148235162435617572891367282110999553789319439912296241889469226304877
c = 22561646796929363815984273658718096881828574147472740106912668949512978818367595303883956088667384207835022579136977262135029404640598574466248596921339941958216824486529066880854722372158998556902335323841170236300423638675072077074005797219260622119718558697081430219981494670569821476853158740209737420919480047033900157150865588466910802691118334480300332681763467974691587834295938999022060676767513865584039532912503921584
p = 33918986475509072603988274492338254523919682179700323084167169617716245684540055969194500298976880885466534900490327133434356902533524212744941101469238500990334546197257933040365697281122571898438913033813040027859
q = 29172702283442199244722211888977987899026182632818103服务器托管55113281879157575741497356945522168552316357276417700368971563177551494320723579146612010452353273237547587402941227901795977981691403950826343318848831462080703
e = 1009*7
def onemod(e, q):
p = random.randint(1, q-1)
while(powmod(p, (q-1)//e, q) == 1): # (r,s)=1
p = random.randint(1, q)
return p
def AMM_rth(o, r, q): # r|(q-1
assert((q-1) % r == 0)
p = onemod(r, q)
t = 0
s = q-1
while(s % r == 0):
s = s//r
t += 1
k = 1
while((s*k+1) % r != 0):
k += 1
alp = (s*k+1)//r
a = powmod(p, r**(t-1)*s, q)
b = powmod(o, r*a-1, q)
c = powmod(p, s, q)
h = 1
for i in range(1, t-1):
d = powmod(int(b), r**(t-1-i), q)
if d == 1:
j = 0
else:
j = (-math.log(d, a)) % r
b = (b*(c**(r*j))) % q
h = (h*c**j) % q
c = (c*r) % q
result = (powmod(o, alp, q)*h)
return result
def ALL_Solution(m, q, rt, cq, e):
mp = []
for pr in rt:
r = (pr*m) % q
# assert(pow(r, e, q) == cq)
mp.append(r)
return mp
def calc(mp, mq, e, p, q):
i = 1
j = 1
t1 = invert(q, p)
t2 = invert(p, q)
for mp1 in mp:
for mq1 in mq:
j += 1
if j % 100000 == 0:
print(j)
ans = (mp1*t1*q+mq1*t2*p) % (p*q)
if check(ans):
return
return
def check(m):
try:
a = long_to_bytes(m)
if b'NSSCTF' in a:
print(a)
return True
else:
return False
except:
return False
def ALL_ROOT2(r, q): # use function set() and .add() ensure that the generated elements are not repeated
li = set()
while(len(li) [RSA3]P11（证书格式）
题目
enc:
Qq/q(o鴽峹^,欗夲b?銁R%f讼?s?碢w溌(浠炓ネ$╀氲?&箄M瑈i:?@]T凿烯邽iAta忀,喌嘦?`糿50?,＇卞w|Zn玪H騲吀D犵key.pem:
-----BEGIN RSA PRIVATE KEY-----
MIICWwIBAAKBgHBkeHn6Q67opdN4V1S3mI0SsUuYzzm+IbXZDz4yZOMWz5nDBYuJ
SA8rRqDtqb7mtNdTGZZx7xe6tOwleqvkXn629mgUZZegyaBdBSPnUR6IUqduqpLo
HRavrHr1IkI6oAmDEQzi1lCZ03x0jMKuoOKp9LBhP9ijCoy9iRh9tH+FAgMBAAEC
gYAvLn5E9oKjUpcKh2Jh9hDcaBR1n9iebOrJ5C059v3TNyg/bFdPlHnjpE8qD5tK
wJ76JbCAL6QnWgHJgJJWxq/EAy/9SG+eApaBo94Sb2B2A1WceDf8F1idkXUOvU/3
kd/wbw/gLZLya8WCFF4SUZx09TToMqSWDEJI4kN17pU5AQJBAJv9ShfSbaMNK31O
kg9LSI7wFLq7iiFRl5kXvSKLsYB3HAKHNlV6/ZL1TV2jg37yf9Mi2f0Gx5AVXbwi
/1ef9R0CQQC4c5EkR8VAw8lqePLwCkCJisXKAEOqPZFOiSCCIVnY+5J4kgiZiS33
rskWwsYAIBHVKiXSy+5NdvWk51MeYi+JAkBiZNvmuOJVVkpXaUcyhH9JQmEhBIj1
yVzBwbqY3trhOMCfS6DXPJRUrYzWgvzAB8Dfcn1kYHFjDkcpFD5SjGB1AkBtyKNH
w8v820tjqu91vbRh6Q4GSBf+GL0G0IlfyrfudPXd+5VQxRxuAkM/39f3tR7IEFkI
2UZSJw7YArMvL2N5AkEAmVGTH6DU3ygzjCtdl4/2dhonSHcEovCFWGZuCqBjYEw6
IGYAlpOiv/BICMXrOBsdd1+4j6n1edxHSGH9q4Aoug==
-----END RSA PRIVATE KEY-----我的解答：
本题我们将来了解关于RSA的证书格式，之前我们所有的题目都是给出具体的数字，然后在这些数字上面做操作，但是在现实世界中不可能直接传输数字来进行操作的，因为这太不稳定了，例如某处出现错误、出现截断、顺序颠倒等等都会导致整个传输过程出现不可查的错误。所以会有统一的格式对这些数字进行封装，而这种封装之后的内容我们就称之为证书。
我们常见的证书有两种格式，一种叫做PEM另一种为DER，实际上不管使用的是哪种格式，证书的内容最后都是我们那些数字，而且我们可以很轻松的在不同的证书之间进行转换。
本题给出了一个.pem的证书，同时给出了enc文件，但是没有给出具体的加密逻辑，此时我们只能先将证书的内容提取出来再做下一步判断。对于这些各类证书，我们都可以使用openssl工具进行提取，
直接输入openssl help你会发现打印出来了命令列表
Standard commands
asn1parse ca ciphers cms
crl crl2pkcs7 dgst dhparam
dsa dsaparam ec ecparam
enc engine errstr gendsa
genpkey genrsa help list
nseq ocsp passwd pkcs12
pkcs7 pkcs8 pkey pkeyparam
pkeyutl prime rand rehash
req rsa rsautl s_client
s_server s_time sess_id smime
speed spkac srp storeutl
cast-cbc cast5-cbc cast5-cfb cast5-ecb
cast5-ofb des des-cbc des-cfb
des-ecb des-ede des-ede-cbc des-ede-cfb
des-ede-ofb des-ede3 des-ede3-cbc des-ede3-cfb
des-ede3-ofb des-ofb des3 desx
idea idea-cbc idea-cfb idea-ecb
idea-ofb rc2 rc2-40-cbc rc2-64-cbc
rc2-cbc rc2-cfb rc2-ecb rc2-ofb
rc4 rc4-40 seed seed-cbc
seed-cfb seed-ecb seed-ofb sm4-cbc
sm4-cfb sm4-ctr sm4-ecb sm4-ofb这里的每一项都代表特定的算法或者证书格式，而我们这里涉及的是rsa，所以我们使用openssl rsa -help进一步查看帮助文档
Usage: rsa [options]
Valid options are:
-help Display this summary 查看帮助
-inform format Input format, one of DER PEM 指定输入格式
-outform format Output format, one of DER PEM PVK 指定输出格式
-in val Input file 输入文件
-out outfile Output file 输出文件
-pubin Expect a public key in input file 期望输入时一个公钥
-pubout Output a public key 输出公钥文件
-passout val Output file pass phrase source 给输出文件设置密码
-passin val Input file pass phrase source 输入文件的密码
-RSAPublicKey_in Input is an RSAPublicKey 指定输入是一个RSA公钥
-RSAPublicKey_out Output is an RSAPublicKey 指定输出是一个RSA公钥
-noout Don't print key out 不要打印输入的密钥内容
-text Print the key in text 用文本格式打印密钥内容
-modulus Print the RSA key modulus 打印RSA密钥的模数
-check Verify key consistency 检测密钥是否一致
-* Any supported cipher 其他参数
-pvk-strong Enable 'Strong' PVK encoding level (default) 启用“强”PVK编码级别（默认）
-pvk-weak Enable 'Weak' PVK encoding level 启用“弱”PVK编码级别
-pvk-none Don't enforce PVK encoding 不强制执行PVK编码
-engine val Use engine, possibly a hardware device 指定解析引擎这里列出了和rsa证书有关的项，后面中文内容是我额外添加的释义，那么我们要查看密钥内容的话直接
openssl rsa -in key.pem -inform PEM
会发现他将密钥内容又打印了一遍，这是因为它默认就是只做解析不会有其他操作，我们需要具体指定我们想要的操作，例如-text以文本内容输出参数，
openssl rsa -in key.pem -inform PEM -text
此时我们得到输出
RSA Private-Key: (1023 bit, 2 primes)
modulus:
70:64:78:79:fa:43:ae:e8:a5:d3:78:57:54:b7:98:
8d:12:b1:4b:98:cf:39:be:21:b5:d9:0f:3e:32:64:
e3:16:cf:99:c3:05:8b:89:48:0f:2b:46:a0:ed:a9:
be:e6:b4:d7:53:19:96:71:ef:17:ba:b4:ec:25:7a:
ab:e4:5e:7e:b6:f6:68:14:65:97:a0:c9:a0:5d:05:
23:e7:51:1e:88:52:a7:6e:aa:92:e8:1d:16:af:ac:
7a:f5:22:42:3a:a0:09:83:11:0c:e2:d6:50:99:d3:
7c:74:8c:c2:ae:a0:e2:a9:f4:b0:61:3f:d8:a3:0a:
8c:bd:89:18:7d:b4:7f:85
publicExponent: 65537 (0x10001)
privateExponent:
2f:2e:7e:44:f6:82:a3:52:97:0a:87:62:61:f6:10:
dc:68:14:75:9f:d8:9e:6c:ea:c9:e4:2d:39:f6:fd:
d3:37:28:3f:6c:57:4f:94:79:e3:a4:4f:2a:0f:9b:
4a:c0:9e:fa:25:b0:80:2f:a4:27:5a:01:c9:80:92:
56:c6:af:c4:03:2f:fd:48:6f:9e:02:96:81:a3:de:
12:6f:60:76:03:55:9c:78:37:fc:17:58:9d:91:75:
0e:bd:4f:f7:91:df:f0:6f:0f:e0:2d:92:f2:6b:c5:
82:14:5e:12:51:9c:74:f5:34:e8:32:a4:96:0c:42:
48:e2:43:75:ee:95:39:01
prime1:
00:9b:fd:4a:17:d2:6d:a3:0d:2b:7d:4e:92:0f:4b:
48:8e:f0:14:ba:bb:8a:21:51:97:99:17:bd:22:8b:
b1:80:77:1c:02:87:36:55:7a:fd:92:f5:4d:5d:a3:
83:7e:f2:7f:d3:22:d9:fd:06:c7:90:15:5d:bc:22:
ff:57:9f:f5:1d
prime2:
00:b8:73:91:24:47:c5:40:c3:c9:6a:78:f2:f0:0a:
40:89:8a:c5:ca:00:43:aa:3d:91:4e:89:20:82:21:
59:d8:fb:92:78:92:08:99:89:2d:f7:ae:c9:16:c2:
c6:00:20:11:d5:2a:25:d2:cb:ee:4d:76:f5:a4:e7:
53:1e:62:2f:89
exponent1:
62:64:db:e6:b8:e2:55:56:4a:57:69:47:32:84:7f:
49:42:61:21:04:88:f5:c9:5c:c1:c1:ba:98:de:da:
e1:38:c0:9f:4b:a0:d7:3c:94:54:ad:8c:d6:82:fc:
c0:07:c0:df:72:7d:64:60:71:63:0e:47:29:14:3e:
52:8c:60:75
exponent2:
6d:c8:a3:47:c3:cb:fc:db:4b:63:aa:ef:75:bd:b4:
61:e9:0e:06:48:17:fe:18:bd:06:d0:89:5f:ca:b7:
ee:74:f5:dd:fb:95:50:c5:1c:6e:02:43:3f:df:d7:
f7:b5:1e:c8:10:59:08:d9:46:52:27:0e:d8:02:b3:
2f:2f:63:79
coefficient:
00:99:51:93:1f:a0:d4:df:28:33:8c:2b:5d:97:8f:
f6:76:1a:27:48:77:04:a2:f0:85:58:66:6e:0a:a0:
63:60:4c:3a:20:66:00:96:93:a2:bf:f0:48:08:c5:
eb:38:1b:1d:77:5f:b8:8f:a9:f5:79:dc:47:48:61:
fd:ab:80:28:ba我们可以看到，它解析出了这个一个RSA的私钥文件，里面包含
modulus - 模数 - n
publicExponent - 加密指数 - e
privateExponent - 解密指数 - d
prime1 - 素因子 - p
prime2 - 素因子 - q可以发现这里面直接包含了我们涉及到的所有RSA参数，除了这些我们已经见过的参数之外，还包含一些其他参数，这些参数是用来进行快速解密的CRT参数，实际上他们分别是
exponent1 - dp
exponent2 - dq
coefficient - invert(p, q)这是一个非常完整的私钥，有时候提取出来的内容并不那么完整，例如只涉及其中的部分参数，此时这需要我们利用得到的参数进一步考察参数之前的关系，再使用我们之前所学习过的各类攻击手段对密文进行解密。
这里的输出实际上就是16进制值，你只需要把所有的:去掉并粘连为一行即可使用。
对于密文的话，我们直接从文件读取然后使用bytes_to_long转为数字处理即可。
from Crypto.Util.number import *
from gmpy2 import *
n = 0x70647879fa43aee8a5d3785754b7988d12b14b98cf39be21b5d90f3e3264e316cf99c3058b89480f2b46a0eda9bee6b4d753199671ef17bab4ec257aabe45e7eb6f668146597a0c9a05d0523e7511e8852a76eaa92e81d16afac7af522423aa00983110ce2d65099d37c748cc2aea0e2a9f4b0613fd8a30a8cbd89187db47f85
c = open('enc', 'rb').read()
c = bytes_to_long(c)
d = 0x2f2e7e44f682a352970a876261f610dc6814759fd89e6ceac9e42d39f6fdd337283f6c574f9479e3a44f2a0f9b4ac09efa25b0802fa4275a01c9809256c6afc4032ffd486f9e029681a3de126f607603559c7837fc17589d91750ebd4ff791dff06f0fe02d92f26bc582145e12519c74f534e832a4960c4248e24375ee953901
print(long_to_bytes(pow(c, d, n)))
# NSSCTF{4f85c39b-6d7a-4e29-a215-7379e30d2939}以上是手动提取字段的方案，实际上在Crypto包中已经包含了关于各类证书的解析，我们也可以使用exp
from Crypto.Util.number import *
from gmpy2 import *
from Crypto.PublicKey import RSA
rsa = RSA.importKey(open('key.pem', 'rb').read())
print(rsa.n, rsa.d, rsa.p) # 提取具体值
c = open('enc', 'rb').read()
c = bytes_to_long(c)
m = rsa._decrypt(c)
print(long_to_bytes(m))
# NSSCTF{4f85c39b-6d7a-4e29-a215-7379e30d2939}关于openssl我们还可以使用它进行转换各类密钥格式，例如我们将密钥转换为DER格式
openssl rsa -in key.pem -inform PEM -outform DER -out key.der
又或者从私钥生成公钥文件
openssl rsa -in key.pem -inform PEM -pubout
[RSA3]P12（证书修复）
题目
enc = 2329206064672111950904450292941421573350591294207157652026787098178545948258554492347649016030892000747909819064473414536692222493030122267884839986067073054508582403564557167583565364976046083954888777809177108315052118912603290095925912298584322873410379937455462434313487981715516761071523410121549134193124709612876311518391130974466069686830456036397449773159386026998482557500868323733155606973727191287617806211911722356975478414165867941665666556476756617951672736466672410799762479373101996896644454778482896784598378016390592459460753042458284030795009957030383305268628413551730442224404807955926606496353
我们还得到了半截密钥，请你解密上述密文
Oh17ELp/n2Urnqg/gaFbKWHgDNYzdPNGqNePgdrRtpfzq+js7QAiYNifLRK8k5XC
MwErb3RKOA0dCu14yftSoo2V+FjGML07Fk6Fe0BvVBMRQm1k1fC24NECgYEAvv/5
kH91u3rVYRMbXHauE3vWeuDjK5D5K5l7BEJ3yrPf64TyVROBJ+Gk5TdRpo23Q6AO
2KzFjzMQf+NdtrSBO8BI20i9UwvLNfukNNu3DifXiu3i3g1HRd81okVBe4x0oxp7
Vad9tF69btHcSz3KpDWnnb9yQNlndTcuZLWLCAMCgYB3pVRhTBEbUd6pA6joIivn
lbRZSIBfxvXqZ+YK1JPxF7MDPqLuhNh8CimofqOJCKk+MT4I/oPckbqGlbqWnUDy
Q63f9iDuQL2oVi/1OJZh79i51ZdrrPK8mhz8VNdwTHCYRBseclN2D8fbzvekFwgu
dJLo4ICPNNgwx3LoAHFPQQKBgBwQBf3qDEVAdetuYD3Eniz0q/2f3yC+iy2RvlZQ
4cLhjMvQ274OQJK4f37CEvgSqFOCR8wkDl7M1ObFZDZ87OP3i3zUgiSaff/veh/e
DFZDGlMqQoP3lXo5omq2HDnn2BdCw85A7qI6rUCECwbvDD/2NitiPooypxW8xs87
MTM7AoGBAISI776nLpq6x/cQhbhukHG+zhcPjJKjh669zIn4kVwzc5YJpzys1VWb
Olb9WQgu0xG6tJ9C6gumvl4lNFPbD8i1tqq0WBY7igExIf1cVU3MUdgcV+YPWdnX
+PTUX6skNl2gOe2PtUAc+v8Miq4hka6L10I1HREDT/Dwwy+wWGgQ
-----END RSA PRIVATE KEY-----我的解答：
在本题中我们得到的是一个破损的证书文件，此时我们无法直接使用openssl提取出想要的信息，但是信息就在里面，所以我们要了解PEM的证书编码格式。
首先我们要知道PEM文件是按照ASN.1标准进行DER编码后再进行Base64编码得到的内容，所以PEM和DER本质是一家，只是在DER的基础上添加了Base64编码。
这里我们先以P11的证书为例来说明其格式，首先我们将证书解Base64后再转换为16进制输出
from base64 import b64decode
import binascii
s = '''MIICWwIBAAKBgHBkeHn6Q67opdN4V1S3mI0SsUuYzzm+IbXZDz4yZOMWz5nDBYuJ
SA8rRqDtqb7mtNdTGZZx7xe6tOwleqvkXn629mgUZZegyaBdBSPnUR6IUqduqpLo
HRavrHr1IkI6oAmDEQzi1lCZ03x0jMKuoOKp9LBhP9ijCoy9iRh9tH+FAgMBAAEC
gYAvLn5E9oKjUpcKh2Jh9hDcaBR1n9iebOrJ5C059v3TNyg/bFdPlHnjpE8qD5tK
wJ76JbCAL6QnWgHJgJJWxq/EAy/9SG+eApaBo94Sb2B2A1WceDf8F1idkXUOvU/3
kd/wbw/gLZLya8WCFF4SUZx09TToMqSWDEJI4kN17pU5AQJBAJv9ShfSbaMNK31O
kg9LSI7wFLq7iiFRl5kXvSKLsYB3HAKHNlV6/ZL1TV2jg37yf9Mi2f0Gx5AVXbwi
/1ef9R0CQQC4c5EkR8VAw8lqePLwCkCJisXKAEOqPZFOiSCCIVnY+5J4kgiZiS33
rskWwsYAIBHVKiXSy+5NdvWk51MeYi+JAkBiZNvmuOJVVkpXaUcyhH9JQmEhBIj1
yVzBwbqY3trhOMCfS6DXPJRUrYzWgvzAB8Dfcn1kYHFjDkcpFD5SjGB1AkBtyKNH
w8v820tjqu91vbRh6Q4GSBf+GL0G0IlfyrfudPXd+5VQxRxuAkM/39f3tR7IEFkI
2UZSJw7YArMvL2N5AkEAmVGTH6DU3ygzjCtdl4/2dhonSHcEovCFWGZuCqBjYEw6
IGYAlpOiv/BICMXrOBsdd1+4j6n1edxHSGH9q4Aoug=='''
s = b64decode(s)
print(binascii.hexlify(s))得到
3082025b02010002818070647879fa43aee8a5d3785754b7988d12b14b98cf39be21b5d90f3e3264e316cf99c3058b89480f2b46a0eda9bee6b4d753199671ef17bab4ec257aabe45e7eb6f668146597a0c9a05d0523e7511e8852a76eaa92e81d16afac7af522423aa00983110ce2d65099d37c748cc2aea0e2a9f4b0613fd8a30a8cbd89187db47f8502030100010281802f2e7e44f682a352970a876261f610dc6814759fd89e6ceac9e42d39f6fdd337283f6c574f9479e3a44f2a0f9b4ac09efa25b0802fa4275a01c9809256c6afc4032ffd486f9e029681a3de126f607603559c7837fc17589d91750ebd4ff791dff06f0fe02d92f26bc582145e12519c74f534e832a4960c4248e24375ee9539010241009bfd4a17d26da30d2b7d4e920f4b488ef014babb8a2151979917bd228bb180771c028736557afd92f54d5da3837ef27fd322d9fd06c790155dbc22ff579ff51d024100b873912447c540c3c96a78f2f00a40898ac5ca0043aa3d914e8920822159d8fb9278920899892df7aec916c2c6002011d52a25d2cbee4d76f5a4e7531e622f8902406264dbe6b8e255564a57694732847f494261210488f5c95cc1c1ba98dedae138c09f4ba0d73c9454ad8cd682fcc007c0df727d646071630e4729143e528c607502406dc8a347c3cbfcdb4b63aaef75bdb461e90e064817fe18bd06d0895fcab7ee74f5ddfb9550c51c6e02433fdfd7f7b51ec8105908d94652270ed802b32f2f63790241009951931fa0d4df28338c2b5d978ff6761a27487704a2f08558666e0aa063604c3a2066009693a2bff04808c5eb381b1d775fb88fa9f579dc474861fdab8028ba这便是原始的ASN.1格式内容，首先我们要知道ASN.1是一种用来描述数据结构的抽象语法，它并不是只用来存储密钥，在ASN.1中你可以自定义你的数据类型和数值约束等条件，你可以把它理解为一种序列化数据的格式。其中数据格式如下
以此往复，所以除了最开始的标识符外，后续的内容都是由
类型 + 长度 + 值 构成的，而这些值根据他们出现的位置不同有着不同的含义，例如最开始出现的值0在PEM中代表版本号信息。
随后的数据值1代表模数。完整顺序如下
版本
模数 - n
加密指数 - e
解密指数 - d
素因子1 - p
素因子2 - q
指数1 - dp
指数2 - dq
系数 - invert(q, p)
其他额外信息在了解了该格式后我们就能对上面的16进制数据直接分段了
标识头 30
总长度 82 025b
版本信息 0201 00
n 028180 70647879fa43aee8a5d3785754b7988d12b14b98cf39be21b5d90f3e3264e316cf99c3058b89480f2b46a0eda9bee6b4d753199671ef17bab4ec257aabe45e7eb6f668146597a0c9a05d0523e7511e8852a76eaa92e81d16afac7af522423aa00983110ce2d65099d37c748cc2aea0e2a9f4b0613fd8a30a8cbd89187db47f85
e 0203 010001
d 028180 2f2e7e44f682a352970a876261f610dc6814759fd89e6ceac9e42d39f6fdd337283f6c574f9479e3a44f2a0f9b4ac09efa25b0802fa4275a01c9809256c6afc4032ffd486f9e029681a3de126f607603559c7837fc17589d91750ebd4ff791dff06f0fe02d92f26bc582145e12519c74f534e832a4960c4248e24375ee953901
p 0241 009bfd4a17d26da30d2b7d4e920f4b488ef014babb8a2151979917bd228bb180771c028736557afd92f54d5da3837ef27fd322d9fd06c790155dbc22ff579ff51d
q 0241 00b873912447c540c3c96a78f2f00a40898ac5ca0043aa3d914e8920822159d8fb9278920899892df7aec916c2c6002011d52a25d2cbee4d76f5a4e7531e622f89
dp 0240 6264dbe6b8e255564a57694732847f494261210488f5c95cc1c1ba98dedae138c09f4ba0d73c9454ad8cd682fcc007c0df727d646071630e4729143e528c6075
dq 0240 6dc8a347c3cbfcdb4b63aaef75bdb461e90e064817fe18bd06d0895fcab7ee74f5ddfb9550c51c6e02433fdfd7f7b51ec8105908d94652270ed802b32f2f6379
inv(q,p) 0241 009951931fa0d4df28338c2b5d978ff6761a27487704a2f08558666e0aa063604c3a2066009693a2bff04808c5eb381b1d775fb88fa9f579dc474861fdab8028ba现在回到本题我们也先进行base64解码得到，因为这里是密钥的后半截，所以我们不能从前往后直接解析，需要先找到一个定位锚点，我们可以按照02先给数据初步分段
3a1d7b10ba7f9f652b9ea83f81a15b2961e00cd63374f346a8d78f81dad1b697f3abe8eced0
02260d89f2d12bc9395c233012b6f744a380d1d0aed78c9fb52a28d95f858c630bd3b164e857b406f541311426d64d5f0b6e0d1
02818100befff9907f75bb7ad561131b5c76ae137bd67ae0e32b90f92b997b044277cab3dfeb84f255138127e1a4e53751a68db743a00ed8acc58f33107fe35db6b4813bc048db48bd530bcb35fba434dbb70e27d78aede2de0d4745df35a245417b8c74a31a7b55a77db45ebd6ed1dc4b3dcaa435a79dbf7240d96775372e64b58b0803
02818077a554614c111b51dea903a8e8222be795b45948805fc6f5ea67e60ad493f117b3033ea2ee84d87c0a29a87ea38908a93e313e08fe83dc91ba8695ba969d40f243addff620ee40bda8562ff5389661efd8b9d5976bacf2bc9a1cfc54d7704c7098441b1e7253760fc7dbcef7a417082e7492e8e0808f34d830c772e800714f41
0281801c1005fdea0c454075eb6e603dc49e2cf4abfd9fdf20be8b2d91be5650e1c2e18ccbd0dbbe0e4092b87f7ec212f812a8538247cc240e5eccd4e6c564367cece3f78b7cd482249a7dffef7a1fde0c56431a532a4283f7957a39a26ab61c39e7d81742c3ce40eea23aad40840b06ef0c3ff6362b623e8a32a715bcc6cf3b31333b
028181008488efbea72e9abac7f71085b86e9071bece170f8c92a387aebdcc89f8915c33739609a73cacd5559b3a56fd59082ed311bab49f42ea0ba6be5e253453db0fc8b5b6aab458163b8a013121fd5c554dcc51d81c57e60f59d9d7f8f4d45fab24365da039ed8fb5401cfaff0c8aae2191ae8bd742351d11034ff0f0c32fb0586810不一定数据中出现了02就代表是数据开始的地方，因为也有可能数据中也包含02，我们要一一检验02后面的长度标识定义的长度时候符合后续数据的长度，我们会发现第一块后面的长度标识以及长度都不符合正常的定义，所以其实第一块这里的02是上一块数据中的内容而非新数据的开始标识。最终我们可以得到
3a1d7b10ba7f9f652b9ea83f81a15b2961e00cd63374f346a8d78f81dad1b697f3abe8eced002260d89f2d12bc9395c233012b6f744a380d1d0aed78c9fb52a28d95f858c630bd3b164e857b406f541311426d64d5f0b6e0d1
q 028181 00befff9907f75bb7ad561131b5c76ae137bd67ae0e32b90f92b997b044277cab3dfeb84f255138127e1a4e53751a68db743a00ed8acc58f33107fe35db6b4813bc048db48bd530bcb35fba434dbb70e27d78aede2de0d4745df35a245417b8c74a31a7b55a77db45ebd6ed1dc4b3dcaa435a79dbf7240d96775372e64b58b0803
dp 028180 77a554614c111b51dea903a8e8222be795b45948805fc6f5ea67e60ad493f117b3033ea2ee84d87c0a29a87ea38908a93e313e08fe83dc91ba8695ba969d40f243addff620ee40bda8562ff5389661efd8b9d5976bacf2bc9a1cfc54d7704c7098441b1e7253760fc7dbcef7a417082e7492e8e0808f34d830c772e800714f41
dq 028180 1c1005fdea0c454075eb6e603dc49e2cf4abfd9fdf20be8b2d91be5650e1c2e18ccbd0dbbe0e4092b87f7ec212f812a8538247cc240e5eccd4e6c564367cece3f78b7cd482249a7dffef7a1fde0c56431a532a4283f7957a39a26ab61c39e7d81742c3ce40eea23aad40840b06ef0c3ff6362b623e8a32a715bcc6cf3b31333b
inv(q,p) 028181 008488efbea72e9abac7f71085b86e9071bece170f8c92a387aebdcc89f8915c33739609a73cacd5559b3a56fd59082ed311bab49f42ea0ba6be5e253453db0fc8b5b6aab458163b8a013121fd5c554dcc51d81c57e60f59d9d7f8f4d45fab24365da039ed8fb5401cfaff0c8aae2191ae8bd742351d11034ff0f0c32fb0586810所以我们发现有用的数据为q,dp,dq,inv(q,p)，显然此时我们连n都没有，但是我们有dq，我们知道它满足
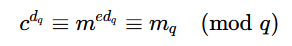
如果我们的m，则此时得到的解mq就等于m。最终exp如下
from Crypto.Util.number import *
q = 0x00befff9907f75bb7ad561131b5c76ae137bd67ae0e32b90f92b997b044277cab3dfeb84f255138127e1a4e53751a68db743a00ed8acc58f33107fe35db6b4813bc048db48bd530bcb35fba434dbb70e27d78aede2de0d4745df35a245417b8c74a31a7b55a77db45ebd6ed1dc4b3dcaa435a79dbf7240d96775372e64b58b0803
dq = 0x1c1005fdea0c454075eb6e603dc49e2cf4abfd9fdf20be8b2d91be5650e1c2e18ccbd0dbbe0e4092b87f7ec212f812a8538247cc240e5eccd4e6c564367cece3f78b7cd482249a7dffef7a1fde0c56431a532a4283f7957a39a26ab61c39e7d81742c3ce40eea23aad40840b06ef0c3ff6362b623e8a32a715bcc6cf3b31333b
c = 2329206064672111950904450292941421573350591294207157652026787098178545948258554492347649016030892000747909819064473414536692222493030122267884839986067073054508582403564557167583565364976046083954888777809177108315052118912603290095925912298584322873410379937455462434313487981715516761071523410121549134193124709612876311518391130974466069686830456036397449773159386026998482557500868323733155606973727191287617806211911722356975478414165867941665666556476756617951672736466672410799762479373101996896644454778482896784598378016390592459460753042458284030795009957030383305268628413551730442224404807955926606496353
m = pow(c, dq, q)
print(long_to_bytes(m))
# NSSCTF{301815bd-67ca-4866-9934-61144503d6b5}所以当得到破损的证书后，我们也能够通过证书格式得到其中的有效信息，再加上其他攻击方法便可以对消息进行解密，当然这里我们得到的是后半截所以可以直接知道每个位置数据代表什么，如果是给出中间部分的证书，此时我们则需要通过逐一分析来进行检验，例如如果数是一个素数，则可能是素因子，如果相邻两个数差的非常大，则可能是e和d，最后我们总能找到有效信息。
服务器托管，北京服务器托管，服务器租用 http://www.fwqtg.net
机房租用，北京机房租用，IDC机房托管， http://www.fwqtg.net
1、配置node环境 Node.js 安装配置—–菜鸟教程 npm 使用介绍—–菜鸟教程 淘宝镜像 淘宝 NPM 镜像是一个完整 npmjs.org 镜像，你可以用此代替官方版本(只读)，同步频率目前为 10分钟 一次以保证尽量与官方服务同步。 可…
