A – 子集和问题
Description
子集和问题的一个实例为〈S,t〉。其中,S={ x1,x2,…,xn}是一个正整数的集合,c是一个正整数。子集和问题判定是否存在S的一个子集S1,使得:
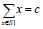
。
试设计一个解子集和问题的回溯法。
对于给定的正整数的集合S={ x1,x2,…,xn}和正整数c,计算S 的一个子集S1,使得:
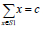
。
Input
输入数据的第1 行有2 个正整数n 和c(n≤10000,c≤10000000),n 表示S 的大小,c是子集和的目标值。接下来的1 行中,有n个正整数,表示集合S中的元素。
Output
将子集和问题的解输出。当问题无解时,输出“No Solution!”。
Samples
Sample #1
Input服务器托管网
Output
5 10 2 2 6 5 4
2 2 6
#include
using namespace std;
const int N = 1e4 + 10;
int a[N];
int ans[N] = {0};
int n, c, sum;
bool flag = 0;
void print(int len){
for(int i = 0; i c || flag) return ;
if(sum == c){
print(len);
flag = 1;
return ;
}
for(int i = x; i > n >> c;
for(int i = 0; i > a[i];
sum += a[i];
}
if(sum B – 运动员最佳匹配问题
Description
羽毛球队有男女运动员各n 人。给定2 个nn 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。
设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
Input
输入数据的第一行有1 个正整数n (1≤n≤20)。接下来的2n 行,每行n个数。前n行是p,后n行是q。
Output
将计算出的男女双方竞赛优势的总和的最大值输出。
Samples
Sample #1
Input
Output
3 10 2 3 2 3 4 3 4 5 2 2 2 3 5 3 4 5 1
52
#include
using namespace std;
const int N = 22;
int n, a[N][N], 服务器托管网b[N][N], vis[N], pre[N], sum;
void dfs(int i, int cnt){
if(i > n && cnt + pre[n] - pre[i-1] > sum){
sum = max(sum, cnt);
return ;
}
if(cnt + pre[n] - pre[i-1] > sum){
for(int j = 1; j > n;
for(int i = 1; i > a[i][j];
}
}
for(int i = 1; i > b[i][j];
}
}
for(int i = 1; i C – 工作分配问题
Description
设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为 cij。试设计一个算法,为每一个人都分配1 件不同的工作,并使总费用达到最小。
设计一个算法,对于给定的工作费用,计算最佳工作分配方案,使总费用达到最小。
Input
输入数据的第一行有1 个正整数n (1≤n≤11)。接下来的n行,每行n个数,表示工作费用。
Output
将计算出的最小总费用输出。
Samples
Sample #1
Input
Output
3 10 2 3 2 3 4 3 4 5
9
#include
using namespace std;
const int N = 25;
const int INF = 0x3f3f3f3f;
int n, ans;
int a[N][N], vis[N];
void dfs(int i, int sum){
if(sum > ans) return ;
if(i == n + 1 && sum > n;
for(int i = 1; i > a[i][j];
}
}
ans = INF;
dfs(1, 0);
cout D – 整数变换问题
Description
整数变换问题。关于整数i的变换f和g定义如下:f(i)=3i;
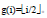
试设计一个算法,对于给定的2 个整数n和m,用最少的f和g变换次数将n变换为m。例如,可以将整数15用4 次变换将它变换为整数4:4=gfgg(15)。当整数n不可能变换为整数m时,算法应如何处理?
对任意给定的整数n和m,计算将整数n变换为整数m所需要的最少变换次数。
Input
输入数据的第一行有2 个正整数n和m。n≤100000,m≤1000000000。
Output
将计算出的最少变换次数以及相应的变换序列输出。第一行是最少变换次数。第2 行是相应的变换序列。
Samples
Sample #1
Input
Output
15 4
4 gfgg
#include
using namespace std;
int maxn, n, m;
char f[101];
int search(int step, int sum){
if(step > maxn) return 0;
if(m == sum * 3 || search(step + 1, sum * 3)){
f[step] = 'f';
return 1;
}
if(sum / 2 == m || search(step+1, sum/2)){
f[step] = 'g';
return 1;
}
return 0;
}
int main()
{
cin >> n >> m;
maxn = 1;
while(!search(1, n)){
maxn ++;
}
cout = 1; i--){
cout 服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net
相关推荐: 大黄蜂($DHF):赋能DeFi生态 迎来黄金时代
未来,可能一切数字资产要围绕着$DHF进行! 在过去的十年中,比特币一直是传统投资者参与加密市场的入场券,也是在经济不稳定的时期非常好的资产配置手段。然而,比特币能否摆脱其作为价值储存的标签并开辟一条新道路还有待观察。 DHF赋能加密货币生态布局 在上一个看涨…

